Enhancing Kernel Flexibility via Learning Asymmetric Locally-Adaptive Kernels

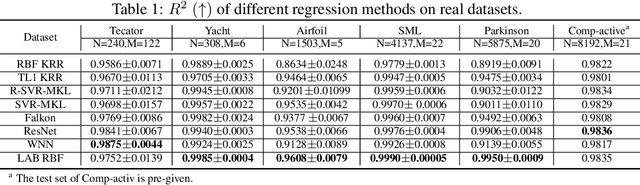
The lack of sufficient flexibility is the key bottleneck of kernel-based learning that relies on manually designed, pre-given, and non-trainable kernels. To enhance kernel flexibility, this paper introduces the concept of Locally-Adaptive-Bandwidths (LAB) as trainable parameters to enhance the Radial Basis Function (RBF) kernel, giving rise to the LAB RBF kernel. The parameters in LAB RBF kernels are data-dependent, and its number can increase with the dataset, allowing for better adaptation to diverse data patterns and enhancing the flexibility of the learned function. This newfound flexibility also brings challenges, particularly with regards to asymmetry and the need for an efficient learning algorithm. To address these challenges, this paper for the first time establishes an asymmetric kernel ridge regression framework and introduces an iterative kernel learning algorithm. This novel approach not only reduces the demand for extensive support data but also significantly improves generalization by training bandwidths on the available training data. Experimental results on real datasets underscore the remarkable performance of the proposed algorithm, showcasing its superior capability in handling large-scale datasets compared to Nystr\"om approximation-based algorithms. Moreover, it demonstrates a significant improvement in regression accuracy over existing kernel-based learning methods and even surpasses residual neural networks.