A Communication-Efficient Distributed Algorithm for Kernel Principal Component Analysis

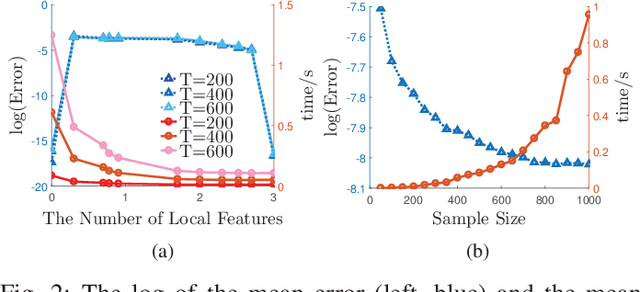
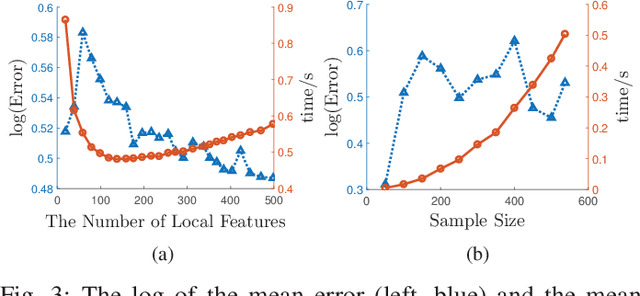
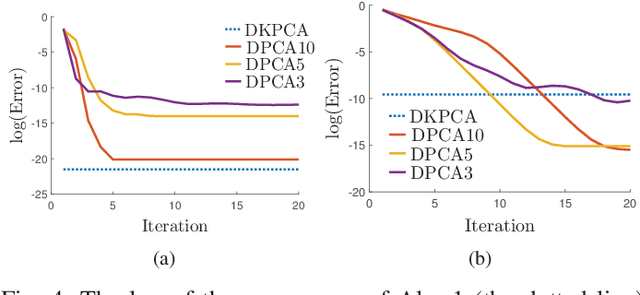
Principal Component Analysis (PCA) is a fundamental technology in machine learning. Nowadays many high-dimension large datasets are acquired in a distributed manner, which precludes the use of centralized PCA due to the high communication cost and privacy risk. Thus, many distributed PCA algorithms are proposed, most of which, however, focus on linear cases. To efficiently extract non-linear features, this brief proposes a communication-efficient distributed kernel PCA algorithm, where linear and RBF kernels are applied. The key is to estimate the global empirical kernel matrix from the eigenvectors of local kernel matrices. The approximate error of the estimators is theoretically analyzed for both linear and RBF kernels. The result suggests that when eigenvalues decay fast, which is common for RBF kernels, the proposed algorithm gives high quality results with low communication cost. Results of simulation experiments verify our theory analysis and experiments on GSE2187 dataset show the effectiveness of the proposed algorithm.