Research advances on fish feeding behavior recognition and intensity quantification methods in aquaculture

As a key part of aquaculture management, fish feeding behavior recognition and intensity quantification has been a hot area of great concern to researchers, and it plays a crucial role in monitoring fish health, guiding baiting work and improving aquaculture efficiency. In order to better carry out the related work in the future, this paper firstly reviews the research advances of fish feeding behavior recognition and intensity quantification methods based on computer vision, acoustics and sensors in a single modality. Then the application of the current emerging multimodal fusion in fish feeding behavior recognition and intensity quantification methods is expounded. Finally, the advantages and disadvantages of various techniques are compared and analyzed, and the future research directions are envisioned.

Learning in Feature Spaces via Coupled Covariances: Asymmetric Kernel SVD and Nyström method

In contrast with Mercer kernel-based approaches as used e.g., in Kernel Principal Component Analysis (KPCA), it was previously shown that Singular Value Decomposition (SVD) inherently relates to asymmetric kernels and Asymmetric Kernel Singular Value Decomposition (KSVD) has been proposed. However, the existing formulation to KSVD cannot work with infinite-dimensional feature mappings, the variational objective can be unbounded, and needs further numerical evaluation and exploration towards machine learning. In this work, i) we introduce a new asymmetric learning paradigm based on coupled covariance eigenproblem (CCE) through covariance operators, allowing infinite-dimensional feature maps. The solution to CCE is ultimately obtained from the SVD of the induced asymmetric kernel matrix, providing links to KSVD. ii) Starting from the integral equations corresponding to a pair of coupled adjoint eigenfunctions, we formalize the asymmetric Nystr\"om method through a finite sample approximation to speed up training. iii) We provide the first empirical evaluations verifying the practical utility and benefits of KSVD and compare with methods resorting to symmetrization or linear SVD across multiple tasks.

SURE: SUrvey REcipes for building reliable and robust deep networks

In this paper, we revisit techniques for uncertainty estimation within deep neural networks and consolidate a suite of techniques to enhance their reliability. Our investigation reveals that an integrated application of diverse techniques--spanning model regularization, classifier and optimization--substantially improves the accuracy of uncertainty predictions in image classification tasks. The synergistic effect of these techniques culminates in our novel SURE approach. We rigorously evaluate SURE against the benchmark of failure prediction, a critical testbed for uncertainty estimation efficacy. Our results showcase a consistently better performance than models that individually deploy each technique, across various datasets and model architectures. When applied to real-world challenges, such as data corruption, label noise, and long-tailed class distribution, SURE exhibits remarkable robustness, delivering results that are superior or on par with current state-of-the-art specialized methods. Particularly on Animal-10N and Food-101N for learning with noisy labels, SURE achieves state-of-the-art performance without any task-specific adjustments. This work not only sets a new benchmark for robust uncertainty estimation but also paves the way for its application in diverse, real-world scenarios where reliability is paramount. Our code is available at \url{https://yutingli0606.github.io/SURE/}.

Self-Attention through Kernel-Eigen Pair Sparse Variational Gaussian Processes

While the great capability of Transformers significantly boosts prediction accuracy, it could also yield overconfident predictions and require calibrated uncertainty estimation, which can be commonly tackled by Gaussian processes (GPs). Existing works apply GPs with symmetric kernels under variational inference to the attention kernel; however, omitting the fact that attention kernels are in essence asymmetric. Moreover, the complexity of deriving the GP posteriors remains high for large-scale data. In this work, we propose Kernel-Eigen Pair Sparse Variational Gaussian Processes (KEP-SVGP) for building uncertainty-aware self-attention where the asymmetry of attention kernels is tackled by Kernel SVD (KSVD) and a reduced complexity is acquired. Through KEP-SVGP, i) the SVGP pair induced by the two sets of singular vectors from KSVD w.r.t. the attention kernel fully characterizes the asymmetry; ii) using only a small set of adjoint eigenfunctions from KSVD, the derivation of SVGP posteriors can be based on the inversion of a diagonal matrix containing singular values, contributing to a reduction in time complexity; iii) an evidence lower bound is derived so that variational parameters can be optimized towards this objective. Experiments verify our excellent performances and efficiency on in-distribution, distribution-shift and out-of-distribution benchmarks.

Primal-Attention: Self-attention through Asymmetric Kernel SVD in Primal Representation

Recently, a new line of works has emerged to understand and improve self-attention in Transformers by treating it as a kernel machine. However, existing works apply the methods for symmetric kernels to the asymmetric self-attention, resulting in a nontrivial gap between the analytical understanding and numerical implementation. In this paper, we provide a new perspective to represent and optimize self-attention through asymmetric Kernel Singular Value Decomposition (KSVD), which is also motivated by the low-rank property of self-attention normally observed in deep layers. Through asymmetric KSVD, $i$) a primal-dual representation of self-attention is formulated, where the optimization objective is cast to maximize the projection variances in the attention outputs; $ii$) a novel attention mechanism, i.e., Primal-Attention, is proposed via the primal representation of KSVD, avoiding explicit computation of the kernel matrix in the dual; $iii$) with KKT conditions, we prove that the stationary solution to the KSVD optimization in Primal-Attention yields a zero-value objective. In this manner, KSVD optimization can be implemented by simply minimizing a regularization loss, so that low-rank property is promoted without extra decomposition. Numerical experiments show state-of-the-art performance of our Primal-Attention with improved efficiency. Moreover, we demonstrate that the deployed KSVD optimization regularizes Primal-Attention with a sharper singular value decay than that of the canonical self-attention, further verifying the great potential of our method. To the best of our knowledge, this is the first work that provides a primal-dual representation for the asymmetric kernel in self-attention and successfully applies it to modeling and optimization.

Jigsaw-ViT: Learning Jigsaw Puzzles in Vision Transformer

The success of Vision Transformer (ViT) in various computer vision tasks has promoted the ever-increasing prevalence of this convolution-free network. The fact that ViT works on image patches makes it potentially relevant to the problem of jigsaw puzzle solving, which is a classical self-supervised task aiming at reordering shuffled sequential image patches back to their natural form. Despite its simplicity, solving jigsaw puzzle has been demonstrated to be helpful for diverse tasks using Convolutional Neural Networks (CNNs), such as self-supervised feature representation learning, domain generalization, and fine-grained classification. In this paper, we explore solving jigsaw puzzle as a self-supervised auxiliary loss in ViT for image classification, named Jigsaw-ViT. We show two modifications that can make Jigsaw-ViT superior to standard ViT: discarding positional embeddings and masking patches randomly. Yet simple, we find that Jigsaw-ViT is able to improve both in generalization and robustness over the standard ViT, which is usually rather a trade-off. Experimentally, we show that adding the jigsaw puzzle branch provides better generalization than ViT on large-scale image classification on ImageNet. Moreover, the auxiliary task also improves robustness to noisy labels on Animal-10N, Food-101N, and Clothing1M as well as adversarial examples. Our implementation is available at https://yingyichen-cyy.github.io/Jigsaw-ViT/.

Compressing Features for Learning with Noisy Labels

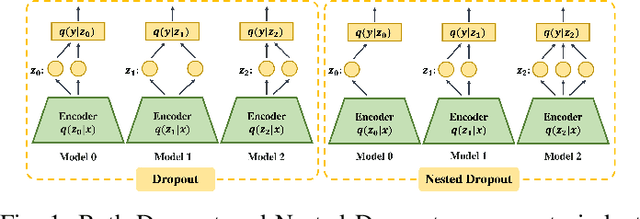
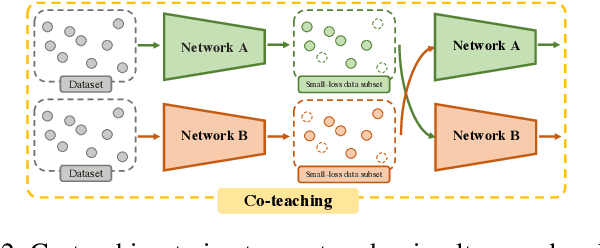
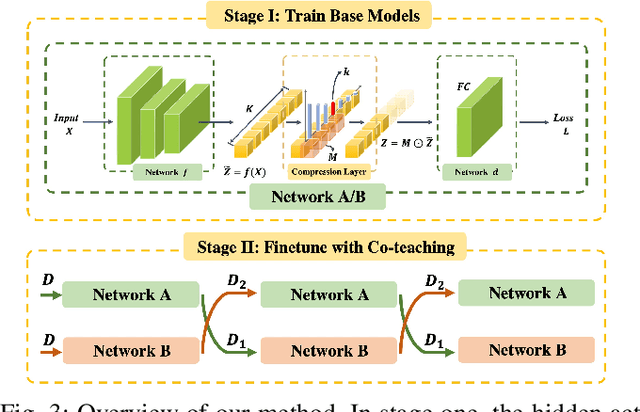
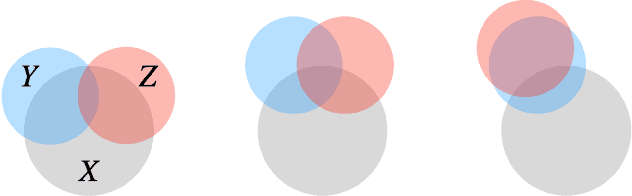
Supervised learning can be viewed as distilling relevant information from input data into feature representations. This process becomes difficult when supervision is noisy as the distilled information might not be relevant. In fact, recent research shows that networks can easily overfit all labels including those that are corrupted, and hence can hardly generalize to clean datasets. In this paper, we focus on the problem of learning with noisy labels and introduce compression inductive bias to network architectures to alleviate this over-fitting problem. More precisely, we revisit one classical regularization named Dropout and its variant Nested Dropout. Dropout can serve as a compression constraint for its feature dropping mechanism, while Nested Dropout further learns ordered feature representations w.r.t. feature importance. Moreover, the trained models with compression regularization are further combined with Co-teaching for performance boost. Theoretically, we conduct bias-variance decomposition of the objective function under compression regularization. We analyze it for both single model and Co-teaching. This decomposition provides three insights: (i) it shows that over-fitting is indeed an issue for learning with noisy labels; (ii) through an information bottleneck formulation, it explains why the proposed feature compression helps in combating label noise; (iii) it gives explanations on the performance boost brought by incorporating compression regularization into Co-teaching. Experiments show that our simple approach can have comparable or even better performance than the state-of-the-art methods on benchmarks with real-world label noise including Clothing1M and ANIMAL-10N. Our implementation is available at https://yingyichen-cyy.github.io/CompressFeatNoisyLabels/.

Boosting Co-teaching with Compression Regularization for Label Noise

In this paper, we study the problem of learning image classification models in the presence of label noise. We revisit a simple compression regularization named Nested Dropout. We find that Nested Dropout, though originally proposed to perform fast information retrieval and adaptive data compression, can properly regularize a neural network to combat label noise. Moreover, owing to its simplicity, it can be easily combined with Co-teaching to further boost the performance. Our final model remains simple yet effective: it achieves comparable or even better performance than the state-of-the-art approaches on two real-world datasets with label noise which are Clothing1M and ANIMAL-10N. On Clothing1M, our approach obtains 74.9% accuracy which is slightly better than that of DivideMix. On ANIMAL-10N, we achieve 84.1% accuracy while the best public result by PLC is 83.4%. We hope that our simple approach can be served as a strong baseline for learning with label noise. Our implementation is available at https://github.com/yingyichen-cyy/Nested-Co-teaching.

Generalizing Random Fourier Features via Generalized Measures

We generalize random Fourier features, that usually require kernel functions to be both stationary and positive definite (PD), to a more general range of non-stationary or/and non-PD kernels, e.g., dot-product kernels on the unit sphere and a linear combination of positive definite kernels. Specifically, we find that the popular neural tangent kernel in two-layer ReLU network, a typical dot-product kernel, is shift-invariant but not positive definite if we consider $\ell_2$-normalized data. By introducing the signed measure, we propose a general framework that covers the above kernels by associating them with specific finite Borel measures, i.e., probability distributions. In this manner, we are able to provide the first random features algorithm to obtain unbiased estimation of these kernels. Experiments on several benchmark datasets verify the effectiveness of our algorithm over the existing methods. Last but not least, our work provides a sufficient and necessary condition, which is also computationally implementable, to solve a long-lasting open question: does any indefinite kernel have a positive decomposition?

Two-stage Best-scored Random Forest for Large-scale Regression

We propose a novel method designed for large-scale regression problems, namely the two-stage best-scored random forest (TBRF). "Best-scored" means to select one regression tree with the best empirical performance out of a certain number of purely random regression tree candidates, and "two-stage" means to divide the original random tree splitting procedure into two: In stage one, the feature space is partitioned into non-overlapping cells; in stage two, child trees grow separately on these cells. The strengths of this algorithm can be summarized as follows: First of all, the pure randomness in TBRF leads to the almost optimal learning rates, and also makes ensemble learning possible, which resolves the boundary discontinuities long plaguing the existing algorithms. Secondly, the two-stage procedure paves the way for parallel computing, leading to computational efficiency. Last but not least, TBRF can serve as an inclusive framework where different mainstream regression strategies such as linear predictor and least squares support vector machines (LS-SVMs) can also be incorporated as value assignment approaches on leaves of the child trees, depending on the characteristics of the underlying data sets. Numerical assessments on comparisons with other state-of-the-art methods on several large-scale real data sets validate the promising prediction accuracy and high computational efficiency of our algorithm.