Class Probability Matching Using Kernel Methods for Label Shift Adaptation

In domain adaptation, covariate shift and label shift problems are two distinct and complementary tasks. In covariate shift adaptation where the differences in data distribution arise from variations in feature probabilities, existing approaches naturally address this problem based on \textit{feature probability matching} (\textit{FPM}). However, for label shift adaptation where the differences in data distribution stem solely from variations in class probability, current methods still use FPM on the $d$-dimensional feature space to estimate the class probability ratio on the one-dimensional label space. To address label shift adaptation more naturally and effectively, inspired by a new representation of the source domain's class probability, we propose a new framework called \textit{class probability matching} (\textit{CPM}) which matches two class probability functions on the one-dimensional label space to estimate the class probability ratio, fundamentally different from FPM operating on the $d$-dimensional feature space. Furthermore, by incorporating the kernel logistic regression into the CPM framework to estimate the conditional probability, we propose an algorithm called \textit{class probability matching using kernel methods} (\textit{CPMKM}) for label shift adaptation. From the theoretical perspective, we establish the optimal convergence rates of CPMKM with respect to the cross-entropy loss for multi-class label shift adaptation. From the experimental perspective, comparisons on real datasets demonstrate that CPMKM outperforms existing FPM-based and maximum-likelihood-based algorithms.

Bagged Regularized $k$-Distances for Anomaly Detection

We consider the paradigm of unsupervised anomaly detection, which involves the identification of anomalies within a dataset in the absence of labeled examples. Though distance-based methods are top-performing for unsupervised anomaly detection, they suffer heavily from the sensitivity to the choice of the number of the nearest neighbors. In this paper, we propose a new distance-based algorithm called bagged regularized $k$-distances for anomaly detection (BRDAD) converting the unsupervised anomaly detection problem into a convex optimization problem. Our BRDAD algorithm selects the weights by minimizing the surrogate risk, i.e., the finite sample bound of the empirical risk of the bagged weighted $k$-distances for density estimation (BWDDE). This approach enables us to successfully address the sensitivity challenge of the hyperparameter choice in distance-based algorithms. Moreover, when dealing with large-scale datasets, the efficiency issues can be addressed by the incorporated bagging technique in our BRDAD algorithm. On the theoretical side, we establish fast convergence rates of the AUC regret of our algorithm and demonstrate that the bagging technique significantly reduces the computational complexity. On the practical side, we conduct numerical experiments on anomaly detection benchmarks to illustrate the insensitivity of parameter selection of our algorithm compared with other state-of-the-art distance-based methods. Moreover, promising improvements are brought by applying the bagging technique in our algorithm on real-world datasets.

Bagged $k$-Distance for Mode-Based Clustering Using the Probability of Localized Level Sets

In this paper, we propose an ensemble learning algorithm named \textit{bagged $k$-distance for mode-based clustering} (\textit{BDMBC}) by putting forward a new measurement called the \textit{probability of localized level sets} (\textit{PLLS}), which enables us to find all clusters for varying densities with a global threshold. On the theoretical side, we show that with a properly chosen number of nearest neighbors $k_D$ in the bagged $k$-distance, the sub-sample size $s$, the bagging rounds $B$, and the number of nearest neighbors $k_L$ for the localized level sets, BDMBC can achieve optimal convergence rates for mode estimation. It turns out that with a relatively small $B$, the sub-sample size $s$ can be much smaller than the number of training data $n$ at each bagging round, and the number of nearest neighbors $k_D$ can be reduced simultaneously. Moreover, we establish optimal convergence results for the level set estimation of the PLLS in terms of Hausdorff distance, which reveals that BDMBC can find localized level sets for varying densities and thus enjoys local adaptivity. On the practical side, we conduct numerical experiments to empirically verify the effectiveness of BDMBC for mode estimation and level set estimation, which demonstrates the promising accuracy and efficiency of our proposed algorithm.

Local Adaptivity of Gradient Boosting in Histogram Transform Ensemble Learning

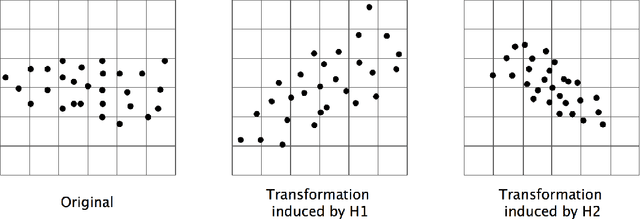
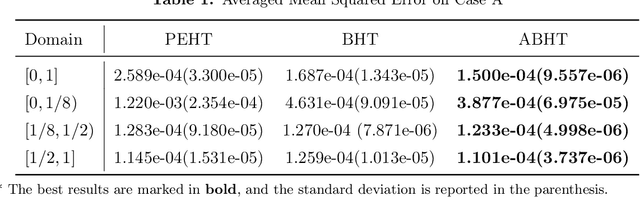
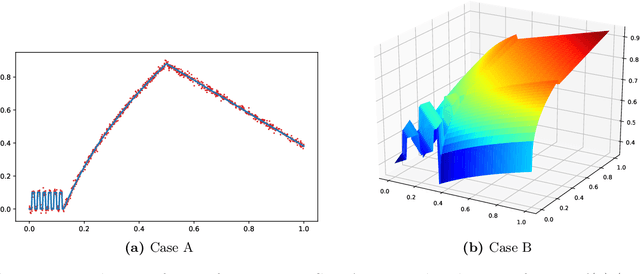
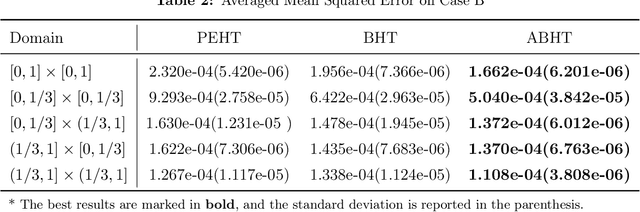
In this paper, we propose a gradient boosting algorithm called \textit{adaptive boosting histogram transform} (\textit{ABHT}) for regression to illustrate the local adaptivity of gradient boosting algorithms in histogram transform ensemble learning. From the theoretical perspective, when the target function lies in a locally H\"older continuous space, we show that our ABHT can filter out the regions with different orders of smoothness. Consequently, we are able to prove that the upper bound of the convergence rates of ABHT is strictly smaller than the lower bound of \textit{parallel ensemble histogram transform} (\textit{PEHT}). In the experiments, both synthetic and real-world data experiments empirically validate the theoretical results, which demonstrates the advantageous performance and local adaptivity of our ABHT.

Under-bagging Nearest Neighbors for Imbalanced Classification

In this paper, we propose an ensemble learning algorithm called \textit{under-bagging $k$-nearest neighbors} (\textit{under-bagging $k$-NN}) for imbalanced classification problems. On the theoretical side, by developing a new learning theory analysis, we show that with properly chosen parameters, i.e., the number of nearest neighbors $k$, the expected sub-sample size $s$, and the bagging rounds $B$, optimal convergence rates for under-bagging $k$-NN can be achieved under mild assumptions w.r.t.~the arithmetic mean (AM) of recalls. Moreover, we show that with a relatively small $B$, the expected sub-sample size $s$ can be much smaller than the number of training data $n$ at each bagging round, and the number of nearest neighbors $k$ can be reduced simultaneously, especially when the data are highly imbalanced, which leads to substantially lower time complexity and roughly the same space complexity. On the practical side, we conduct numerical experiments to verify the theoretical results on the benefits of the under-bagging technique by the promising AM performance and efficiency of our proposed algorithm.

GBHT: Gradient Boosting Histogram Transform for Density Estimation

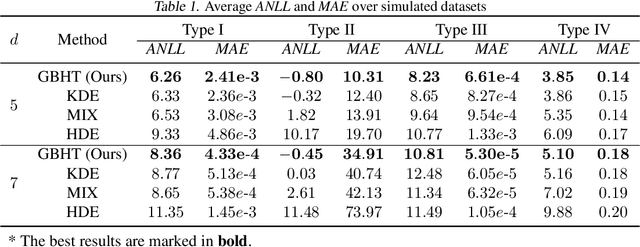
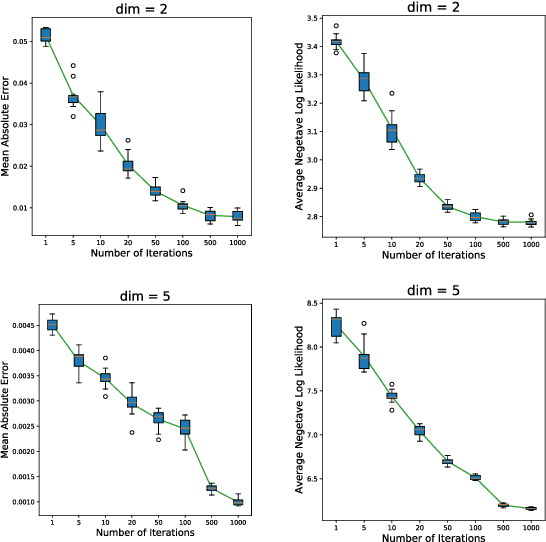
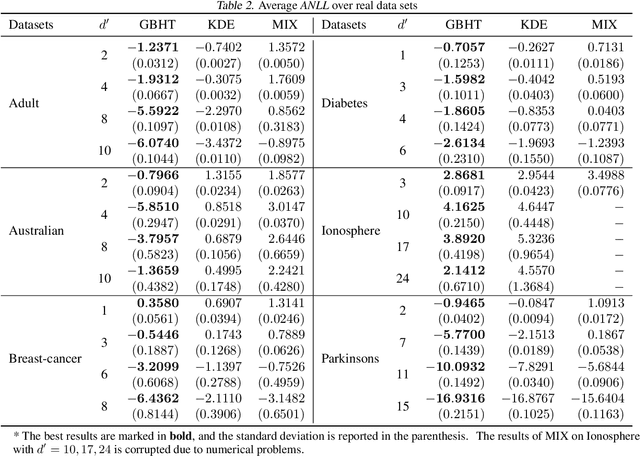
In this paper, we propose a density estimation algorithm called \textit{Gradient Boosting Histogram Transform} (GBHT), where we adopt the \textit{Negative Log Likelihood} as the loss function to make the boosting procedure available for the unsupervised tasks. From a learning theory viewpoint, we first prove fast convergence rates for GBHT with the smoothness assumption that the underlying density function lies in the space $C^{0,\alpha}$. Then when the target density function lies in spaces $C^{1,\alpha}$, we present an upper bound for GBHT which is smaller than the lower bound of its corresponding base learner, in the sense of convergence rates. To the best of our knowledge, we make the first attempt to theoretically explain why boosting can enhance the performance of its base learners for density estimation problems. In experiments, we not only conduct performance comparisons with the widely used KDE, but also apply GBHT to anomaly detection to showcase a further application of GBHT.

Leveraged Weighted Loss for Partial Label Learning

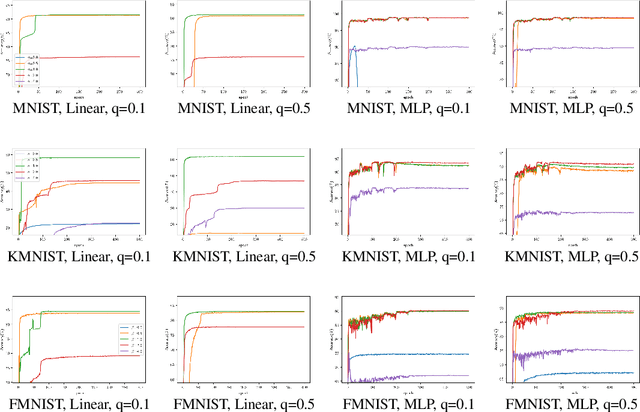
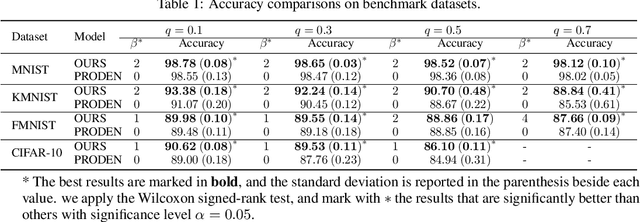
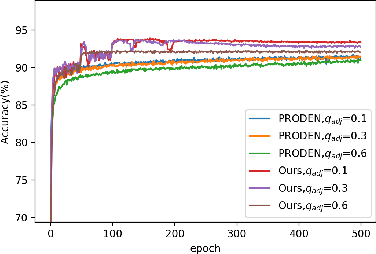
As an important branch of weakly supervised learning, partial label learning deals with data where each instance is assigned with a set of candidate labels, whereas only one of them is true. Despite many methodology studies on learning from partial labels, there still lacks theoretical understandings of their risk consistent properties under relatively weak assumptions, especially on the link between theoretical results and the empirical choice of parameters. In this paper, we propose a family of loss functions named \textit{Leveraged Weighted} (LW) loss, which for the first time introduces the leverage parameter $\beta$ to consider the trade-off between losses on partial labels and non-partial ones. From the theoretical side, we derive a generalized result of risk consistency for the LW loss in learning from partial labels, based on which we provide guidance to the choice of the leverage parameter $\beta$. In experiments, we verify the theoretical guidance, and show the high effectiveness of our proposed LW loss on both benchmark and real datasets compared with other state-of-the-art partial label learning algorithms.

Gradient Boosted Binary Histogram Ensemble for Large-scale Regression

In this paper, we propose a gradient boosting algorithm for large-scale regression problems called \textit{Gradient Boosted Binary Histogram Ensemble} (GBBHE) based on binary histogram partition and ensemble learning. From the theoretical perspective, by assuming the H\"{o}lder continuity of the target function, we establish the statistical convergence rate of GBBHE in the space $C^{0,\alpha}$ and $C^{1,0}$, where a lower bound of the convergence rate for the base learner demonstrates the advantage of boosting. Moreover, in the space $C^{1,0}$, we prove that the number of iterations to achieve the fast convergence rate can be reduced by using ensemble regressor as the base learner, which improves the computational efficiency. In the experiments, compared with other state-of-the-art algorithms such as gradient boosted regression tree (GBRT), Breiman's forest, and kernel-based methods, our GBBHE algorithm shows promising performance with less running time on large-scale datasets.

Histogram Transform Ensembles for Large-scale Regression

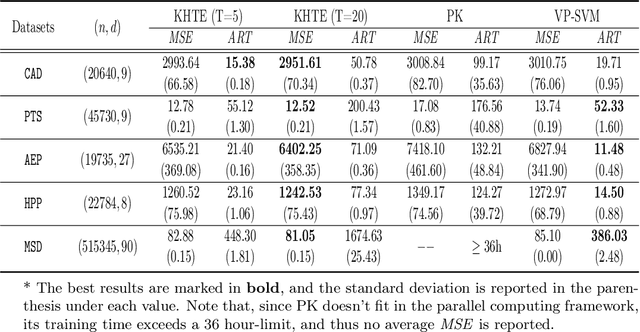
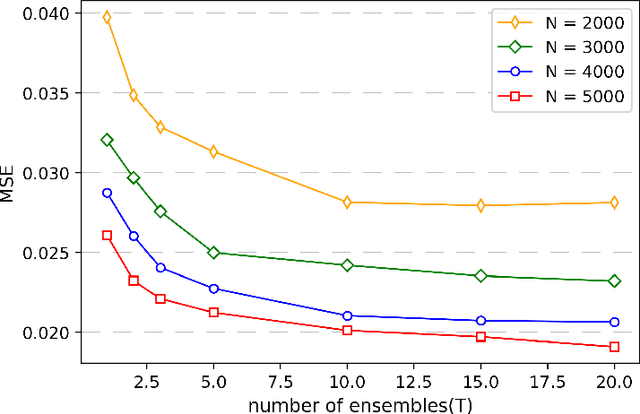
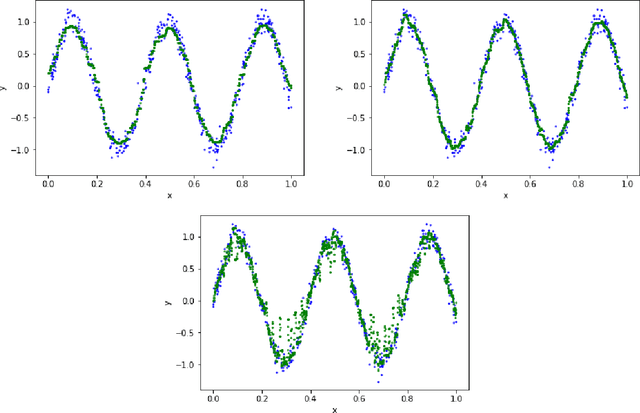
We propose a novel algorithm for large-scale regression problems named histogram transform ensembles (HTE), composed of random rotations, stretchings, and translations. First of all, we investigate the theoretical properties of HTE when the regression function lies in the H\"{o}lder space $C^{k,\alpha}$, $k \in \mathbb{N}_0$, $\alpha \in (0,1]$. In the case that $k=0, 1$, we adopt the constant regressors and develop the na\"{i}ve histogram transforms (NHT). Within the space $C^{0,\alpha}$, although almost optimal convergence rates can be derived for both single and ensemble NHT, we fail to show the benefits of ensembles over single estimators theoretically. In contrast, in the subspace $C^{1,\alpha}$, we prove that if $d \geq 2(1+\alpha)/\alpha$, the lower bound of the convergence rates for single NHT turns out to be worse than the upper bound of the convergence rates for ensemble NHT. In the other case when $k \geq 2$, the NHT may no longer be appropriate in predicting smoother regression functions. Instead, we apply kernel histogram transforms (KHT) equipped with smoother regressors such as support vector machines (SVMs), and it turns out that both single and ensemble KHT enjoy almost optimal convergence rates. Then we validate the above theoretical results by numerical experiments. On the one hand, simulations are conducted to elucidate that ensemble NHT outperform single NHT. On the other hand, the effects of bin sizes on accuracy of both NHT and KHT also accord with theoretical analysis. Last but not least, in the real-data experiments, comparisons between the ensemble KHT, equipped with adaptive histogram transforms, and other state-of-the-art large-scale regression estimators verify the effectiveness and accuracy of our algorithm.

Histogram Transform Ensembles for Density Estimation

We investigate an algorithm named histogram transform ensembles (HTE) density estimator whose effectiveness is supported by both solid theoretical analysis and significant experimental performance. On the theoretical side, by decomposing the error term into approximation error and estimation error, we are able to conduct the following analysis: First of all, we establish the universal consistency under $L_1(\mu)$-norm. Secondly, under the assumption that the underlying density function resides in the H\"{o}lder space $C^{0,\alpha}$, we prove almost optimal convergence rates for both single and ensemble density estimators under $L_1(\mu)$-norm and $L_{\infty}(\mu)$-norm for different tail distributions, whereas in contrast, for its subspace $C^{1,\alpha}$ consisting of smoother functions, almost optimal convergence rates can only be established for the ensembles and the lower bound of the single estimators illustrates the benefits of ensembles over single density estimators. In the experiments, we first carry out simulations to illustrate that histogram transform ensembles surpass single histogram transforms, which offers powerful evidence to support the theoretical results in the space $C^{1,\alpha}$. Moreover, to further exert the experimental performances, we propose an adaptive version of HTE and study the parameters by generating several synthetic datasets with diversities in dimensions and distributions. Last but not least, real data experiments with other state-of-the-art density estimators demonstrate the accuracy of the adaptive HTE algorithm.