Local Adaptivity of Gradient Boosting in Histogram Transform Ensemble Learning
Paper and Code
Dec 05, 2021
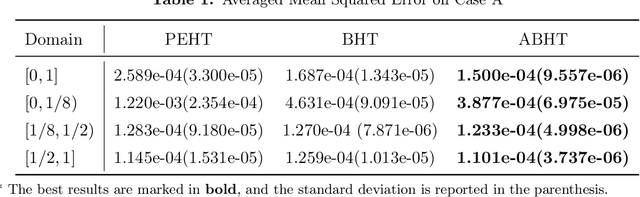
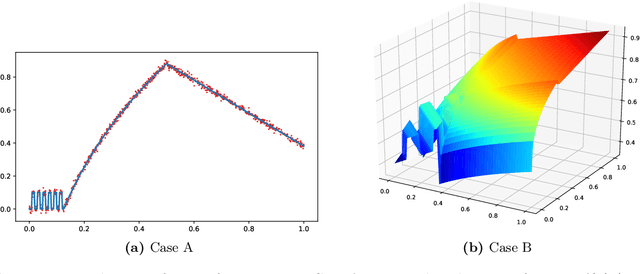
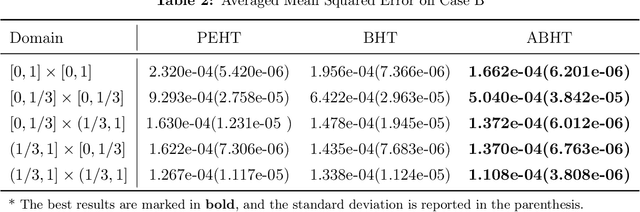
In this paper, we propose a gradient boosting algorithm called \textit{adaptive boosting histogram transform} (\textit{ABHT}) for regression to illustrate the local adaptivity of gradient boosting algorithms in histogram transform ensemble learning. From the theoretical perspective, when the target function lies in a locally H\"older continuous space, we show that our ABHT can filter out the regions with different orders of smoothness. Consequently, we are able to prove that the upper bound of the convergence rates of ABHT is strictly smaller than the lower bound of \textit{parallel ensemble histogram transform} (\textit{PEHT}). In the experiments, both synthetic and real-world data experiments empirically validate the theoretical results, which demonstrates the advantageous performance and local adaptivity of our ABHT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge