Understanding Difficult-to-learn Examples in Contrastive Learning: A Theoretical Framework for Spectral Contrastive Learning

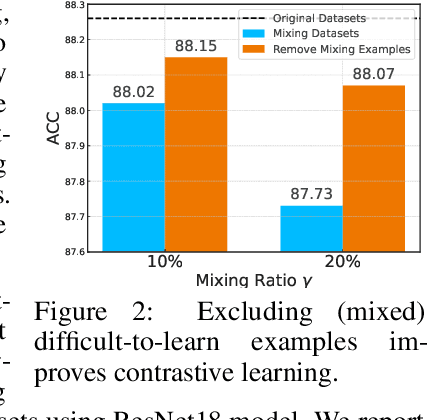
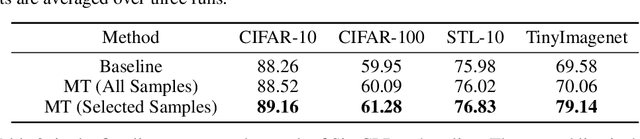
Unsupervised contrastive learning has shown significant performance improvements in recent years, often approaching or even rivaling supervised learning in various tasks. However, its learning mechanism is fundamentally different from that of supervised learning. Previous works have shown that difficult-to-learn examples (well-recognized in supervised learning as examples around the decision boundary), which are essential in supervised learning, contribute minimally in unsupervised settings. In this paper, perhaps surprisingly, we find that the direct removal of difficult-to-learn examples, although reduces the sample size, can boost the downstream classification performance of contrastive learning. To uncover the reasons behind this, we develop a theoretical framework modeling the similarity between different pairs of samples. Guided by this theoretical framework, we conduct a thorough theoretical analysis revealing that the presence of difficult-to-learn examples negatively affects the generalization of contrastive learning. Furthermore, we demonstrate that the removal of these examples, and techniques such as margin tuning and temperature scaling can enhance its generalization bounds, thereby improving performance. Empirically, we propose a simple and efficient mechanism for selecting difficult-to-learn examples and validate the effectiveness of the aforementioned methods, which substantiates the reliability of our proposed theoretical framework.

An Inclusive Theoretical Framework of Robust Supervised Contrastive Loss against Label Noise

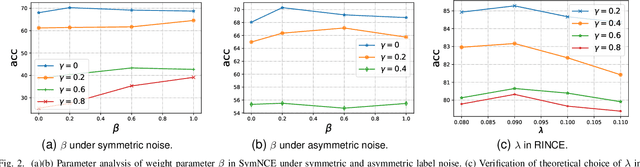
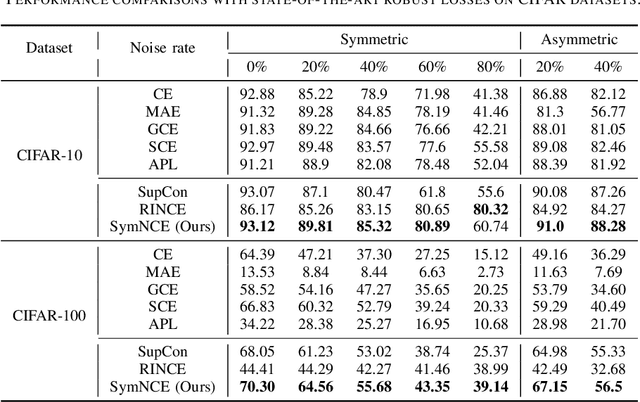
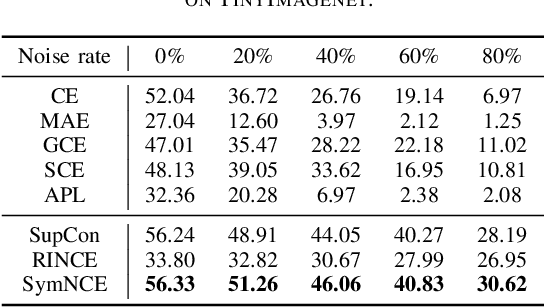
Learning from noisy labels is a critical challenge in machine learning, with vast implications for numerous real-world scenarios. While supervised contrastive learning has recently emerged as a powerful tool for navigating label noise, many existing solutions remain heuristic, often devoid of a systematic theoretical foundation for crafting robust supervised contrastive losses. To address the gap, in this paper, we propose a unified theoretical framework for robust losses under the pairwise contrastive paradigm. In particular, we for the first time derive a general robust condition for arbitrary contrastive losses, which serves as a criterion to verify the theoretical robustness of a supervised contrastive loss against label noise. The theory indicates that the popular InfoNCE loss is in fact non-robust, and accordingly inspires us to develop a robust version of InfoNCE, termed Symmetric InfoNCE (SymNCE). Moreover, we highlight that our theory is an inclusive framework that provides explanations to prior robust techniques such as nearest-neighbor (NN) sample selection and robust contrastive loss. Validation experiments on benchmark datasets demonstrate the superiority of SymNCE against label noise.

Beyond Interpretability: The Gains of Feature Monosemanticity on Model Robustness

Deep learning models often suffer from a lack of interpretability due to polysemanticity, where individual neurons are activated by multiple unrelated semantics, resulting in unclear attributions of model behavior. Recent advances in monosemanticity, where neurons correspond to consistent and distinct semantics, have significantly improved interpretability but are commonly believed to compromise accuracy. In this work, we challenge the prevailing belief of the accuracy-interpretability tradeoff, showing that monosemantic features not only enhance interpretability but also bring concrete gains in model performance. Across multiple robust learning scenarios-including input and label noise, few-shot learning, and out-of-domain generalization-our results show that models leveraging monosemantic features significantly outperform those relying on polysemantic features. Furthermore, we provide empirical and theoretical understandings on the robustness gains of feature monosemanticity. Our preliminary analysis suggests that monosemanticity, by promoting better separation of feature representations, leads to more robust decision boundaries. This diverse evidence highlights the generality of monosemanticity in improving model robustness. As a first step in this new direction, we embark on exploring the learning benefits of monosemanticity beyond interpretability, supporting the long-standing hypothesis of linking interpretability and robustness. Code is available at \url{https://github.com/PKU-ML/Beyond_Interpretability}.

Rethinking Weak Supervision in Helping Contrastive Learning

Contrastive learning has shown outstanding performances in both supervised and unsupervised learning, and has recently been introduced to solve weakly supervised learning problems such as semi-supervised learning and noisy label learning. Despite the empirical evidence showing that semi-supervised labels improve the representations of contrastive learning, it remains unknown if noisy supervised information can be directly used in training instead of after manual denoising. Therefore, to explore the mechanical differences between semi-supervised and noisy-labeled information in helping contrastive learning, we establish a unified theoretical framework of contrastive learning under weak supervision. Specifically, we investigate the most intuitive paradigm of jointly training supervised and unsupervised contrastive losses. By translating the weakly supervised information into a similarity graph under the framework of spectral clustering based on the posterior probability of weak labels, we establish the downstream classification error bound. We prove that semi-supervised labels improve the downstream error bound whereas noisy labels have limited effects under such a paradigm. Our theoretical findings here provide new insights for the community to rethink the role of weak supervision in helping contrastive learning.

GBHT: Gradient Boosting Histogram Transform for Density Estimation

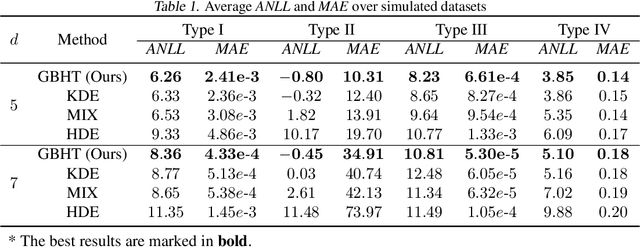
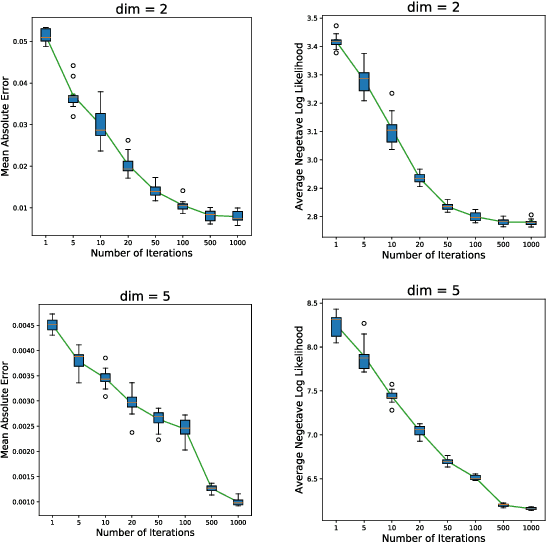
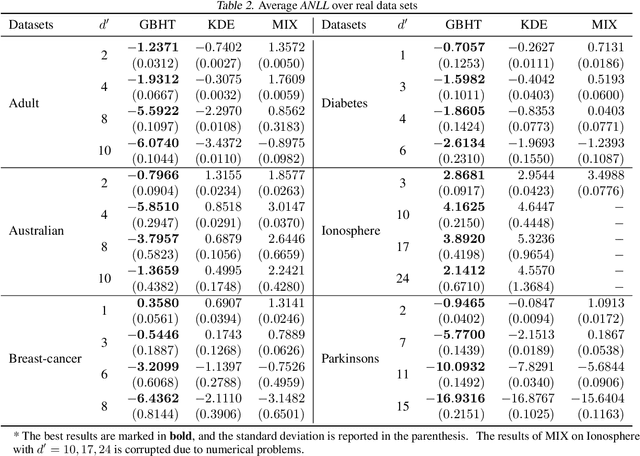
In this paper, we propose a density estimation algorithm called \textit{Gradient Boosting Histogram Transform} (GBHT), where we adopt the \textit{Negative Log Likelihood} as the loss function to make the boosting procedure available for the unsupervised tasks. From a learning theory viewpoint, we first prove fast convergence rates for GBHT with the smoothness assumption that the underlying density function lies in the space $C^{0,\alpha}$. Then when the target density function lies in spaces $C^{1,\alpha}$, we present an upper bound for GBHT which is smaller than the lower bound of its corresponding base learner, in the sense of convergence rates. To the best of our knowledge, we make the first attempt to theoretically explain why boosting can enhance the performance of its base learners for density estimation problems. In experiments, we not only conduct performance comparisons with the widely used KDE, but also apply GBHT to anomaly detection to showcase a further application of GBHT.

Leveraged Weighted Loss for Partial Label Learning

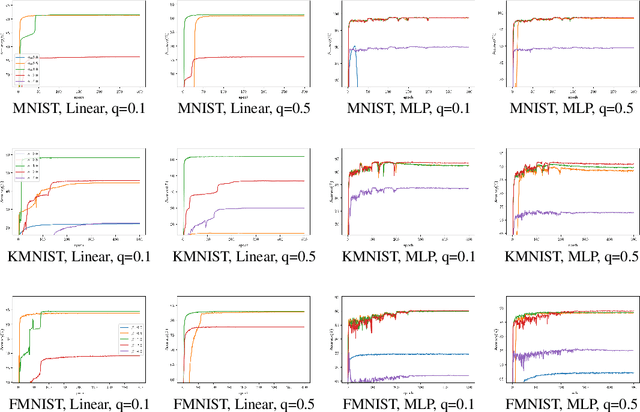
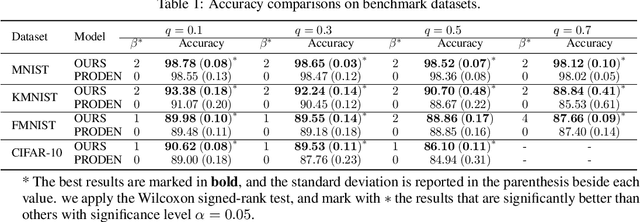
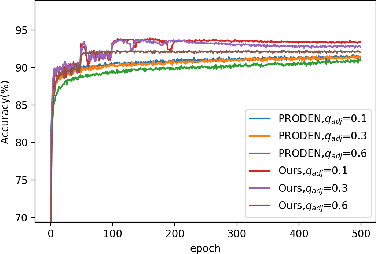
As an important branch of weakly supervised learning, partial label learning deals with data where each instance is assigned with a set of candidate labels, whereas only one of them is true. Despite many methodology studies on learning from partial labels, there still lacks theoretical understandings of their risk consistent properties under relatively weak assumptions, especially on the link between theoretical results and the empirical choice of parameters. In this paper, we propose a family of loss functions named \textit{Leveraged Weighted} (LW) loss, which for the first time introduces the leverage parameter $\beta$ to consider the trade-off between losses on partial labels and non-partial ones. From the theoretical side, we derive a generalized result of risk consistency for the LW loss in learning from partial labels, based on which we provide guidance to the choice of the leverage parameter $\beta$. In experiments, we verify the theoretical guidance, and show the high effectiveness of our proposed LW loss on both benchmark and real datasets compared with other state-of-the-art partial label learning algorithms.