An Augmentation-Aware Theory for Self-Supervised Contrastive Learning

Self-supervised contrastive learning has emerged as a powerful tool in machine learning and computer vision to learn meaningful representations from unlabeled data. Meanwhile, its empirical success has encouraged many theoretical studies to reveal the learning mechanisms. However, in the existing theoretical research, the role of data augmentation is still under-exploited, especially the effects of specific augmentation types. To fill in the blank, we for the first time propose an augmentation-aware error bound for self-supervised contrastive learning, showing that the supervised risk is bounded not only by the unsupervised risk, but also explicitly by a trade-off induced by data augmentation. Then, under a novel semantic label assumption, we discuss how certain augmentation methods affect the error bound. Lastly, we conduct both pixel- and representation-level experiments to verify our proposed theoretical results.

On the Robustness of Kernel Ridge Regression Using the Cauchy Loss Function

Robust regression aims to develop methods for estimating an unknown regression function in the presence of outliers, heavy-tailed distributions, or contaminated data, which can severely impact performance. Most existing theoretical results in robust regression assume that the noise has a finite absolute mean, an assumption violated by certain distributions, such as Cauchy and some Pareto noise. In this paper, we introduce a generalized Cauchy noise framework that accommodates all noise distributions with finite moments of any order, even when the absolute mean is infinite. Within this framework, we study the \textit{kernel Cauchy ridge regressor} (\textit{KCRR}), which minimizes a regularized empirical Cauchy risk to achieve robustness. To derive the $L_2$-risk bound for KCRR, we establish a connection between the excess Cauchy risk and $L_2$-risk for sufficiently large scale parameters of the Cauchy loss, which reveals that these two risks are equivalent. Furthermore, under the assumption that the regression function satisfies H\"older smoothness, we derive excess Cauchy risk bounds for KCRR, showing improved performance as the scale parameter decreases. By considering the twofold effect of the scale parameter on the excess Cauchy risk and its equivalence with the $L_2$-risk, we establish the almost minimax-optimal convergence rate for KCRR in terms of $L_2$-risk, highlighting the robustness of the Cauchy loss in handling various types of noise. Finally, we validate the effectiveness of KCRR through experiments on both synthetic and real-world datasets under diverse noise corruption scenarios.

Median of Forests for Robust Density Estimation

Robust density estimation refers to the consistent estimation of the density function even when the data is contaminated by outliers. We find that existing forest density estimation at a certain point is inherently resistant to the outliers outside the cells containing the point, which we call \textit{non-local outliers}, but not resistant to the rest \textit{local outliers}. To achieve robustness against all outliers, we propose an ensemble learning algorithm called \textit{medians of forests for robust density estimation} (\textit{MFRDE}), which adopts a pointwise median operation on forest density estimators fitted on subsampled datasets. Compared to existing robust kernel-based methods, MFRDE enables us to choose larger subsampling sizes, sacrificing less accuracy for density estimation while achieving robustness. On the theoretical side, we introduce the local outlier exponent to quantify the number of local outliers. Under this exponent, we show that even if the number of outliers reaches a certain polynomial order in the sample size, MFRDE is able to achieve almost the same convergence rate as the same algorithm on uncontaminated data, whereas robust kernel-based methods fail. On the practical side, real data experiments show that MFRDE outperforms existing robust kernel-based methods. Moreover, we apply MFRDE to anomaly detection to showcase a further application.

Class Probability Matching Using Kernel Methods for Label Shift Adaptation

In domain adaptation, covariate shift and label shift problems are two distinct and complementary tasks. In covariate shift adaptation where the differences in data distribution arise from variations in feature probabilities, existing approaches naturally address this problem based on \textit{feature probability matching} (\textit{FPM}). However, for label shift adaptation where the differences in data distribution stem solely from variations in class probability, current methods still use FPM on the $d$-dimensional feature space to estimate the class probability ratio on the one-dimensional label space. To address label shift adaptation more naturally and effectively, inspired by a new representation of the source domain's class probability, we propose a new framework called \textit{class probability matching} (\textit{CPM}) which matches two class probability functions on the one-dimensional label space to estimate the class probability ratio, fundamentally different from FPM operating on the $d$-dimensional feature space. Furthermore, by incorporating the kernel logistic regression into the CPM framework to estimate the conditional probability, we propose an algorithm called \textit{class probability matching using kernel methods} (\textit{CPMKM}) for label shift adaptation. From the theoretical perspective, we establish the optimal convergence rates of CPMKM with respect to the cross-entropy loss for multi-class label shift adaptation. From the experimental perspective, comparisons on real datasets demonstrate that CPMKM outperforms existing FPM-based and maximum-likelihood-based algorithms.

Leveraged Weighted Loss for Partial Label Learning

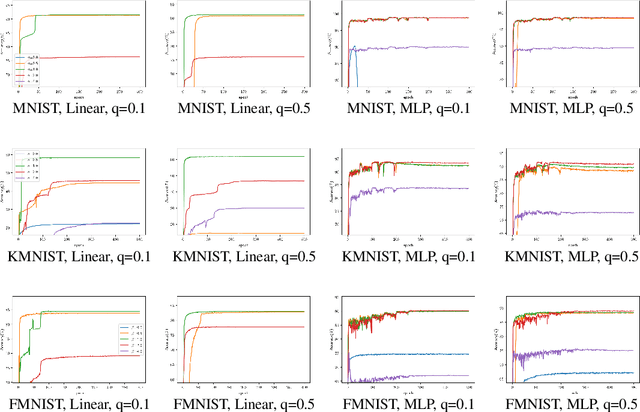
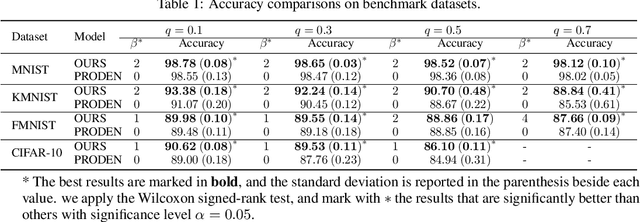
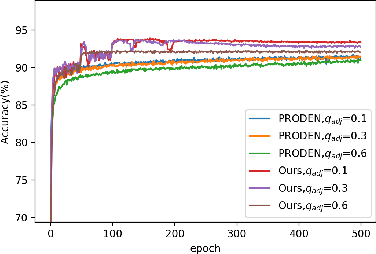
As an important branch of weakly supervised learning, partial label learning deals with data where each instance is assigned with a set of candidate labels, whereas only one of them is true. Despite many methodology studies on learning from partial labels, there still lacks theoretical understandings of their risk consistent properties under relatively weak assumptions, especially on the link between theoretical results and the empirical choice of parameters. In this paper, we propose a family of loss functions named \textit{Leveraged Weighted} (LW) loss, which for the first time introduces the leverage parameter $\beta$ to consider the trade-off between losses on partial labels and non-partial ones. From the theoretical side, we derive a generalized result of risk consistency for the LW loss in learning from partial labels, based on which we provide guidance to the choice of the leverage parameter $\beta$. In experiments, we verify the theoretical guidance, and show the high effectiveness of our proposed LW loss on both benchmark and real datasets compared with other state-of-the-art partial label learning algorithms.

Histogram Transform Ensembles for Large-scale Regression

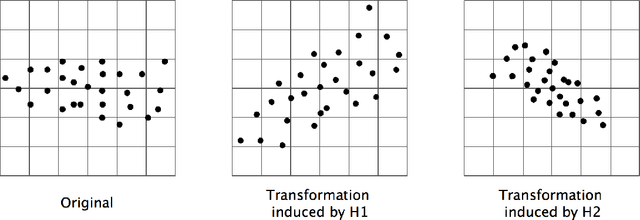
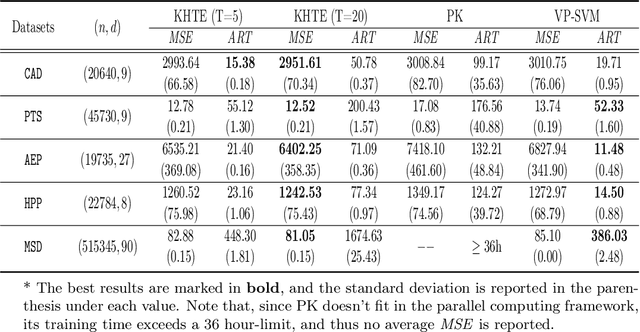
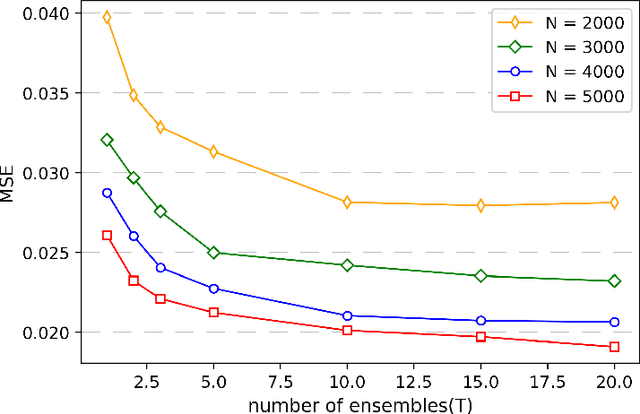
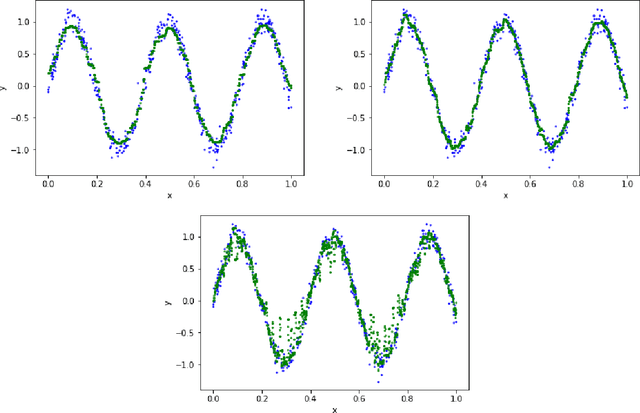
We propose a novel algorithm for large-scale regression problems named histogram transform ensembles (HTE), composed of random rotations, stretchings, and translations. First of all, we investigate the theoretical properties of HTE when the regression function lies in the H\"{o}lder space $C^{k,\alpha}$, $k \in \mathbb{N}_0$, $\alpha \in (0,1]$. In the case that $k=0, 1$, we adopt the constant regressors and develop the na\"{i}ve histogram transforms (NHT). Within the space $C^{0,\alpha}$, although almost optimal convergence rates can be derived for both single and ensemble NHT, we fail to show the benefits of ensembles over single estimators theoretically. In contrast, in the subspace $C^{1,\alpha}$, we prove that if $d \geq 2(1+\alpha)/\alpha$, the lower bound of the convergence rates for single NHT turns out to be worse than the upper bound of the convergence rates for ensemble NHT. In the other case when $k \geq 2$, the NHT may no longer be appropriate in predicting smoother regression functions. Instead, we apply kernel histogram transforms (KHT) equipped with smoother regressors such as support vector machines (SVMs), and it turns out that both single and ensemble KHT enjoy almost optimal convergence rates. Then we validate the above theoretical results by numerical experiments. On the one hand, simulations are conducted to elucidate that ensemble NHT outperform single NHT. On the other hand, the effects of bin sizes on accuracy of both NHT and KHT also accord with theoretical analysis. Last but not least, in the real-data experiments, comparisons between the ensemble KHT, equipped with adaptive histogram transforms, and other state-of-the-art large-scale regression estimators verify the effectiveness and accuracy of our algorithm.

Best-scored Random Forest Density Estimation

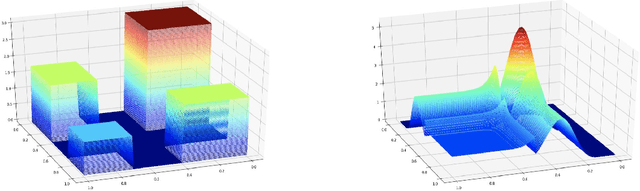
This paper presents a brand new nonparametric density estimation strategy named the best-scored random forest density estimation whose effectiveness is supported by both solid theoretical analysis and significant experimental performance. The terminology best-scored stands for selecting one density tree with the best estimation performance out of a certain number of purely random density tree candidates and we then name the selected one the best-scored random density tree. In this manner, the ensemble of these selected trees that is the best-scored random density forest can achieve even better estimation results than simply integrating trees without selection. From the theoretical perspective, by decomposing the error term into two, we are able to carry out the following analysis: First of all, we establish the consistency of the best-scored random density trees under $L_1$-norm. Secondly, we provide the convergence rates of them under $L_1$-norm concerning with three different tail assumptions, respectively. Thirdly, the convergence rates under $L_{\infty}$-norm is presented. Last but not least, we also achieve the above convergence rates analysis for the best-scored random density forest. When conducting comparative experiments with other state-of-the-art density estimation approaches on both synthetic and real data sets, it turns out that our algorithm has not only significant advantages in terms of estimation accuracy over other methods, but also stronger resistance to the curse of dimensionality.