Locally Private Nonparametric Contextual Multi-armed Bandits

Motivated by privacy concerns in sequential decision-making on sensitive data, we address the challenge of nonparametric contextual multi-armed bandits (MAB) under local differential privacy (LDP). We develop a uniform-confidence-bound-type estimator, showing its minimax optimality supported by a matching minimax lower bound. We further consider the case where auxiliary datasets are available, subject also to (possibly heterogeneous) LDP constraints. Under the widely-used covariate shift framework, we propose a jump-start scheme to effectively utilize the auxiliary data, the minimax optimality of which is further established by a matching lower bound. Comprehensive experiments on both synthetic and real-world datasets validate our theoretical results and underscore the effectiveness of the proposed methods.

Learning to Retrieve and Reason on Knowledge Graph through Active Self-Reflection

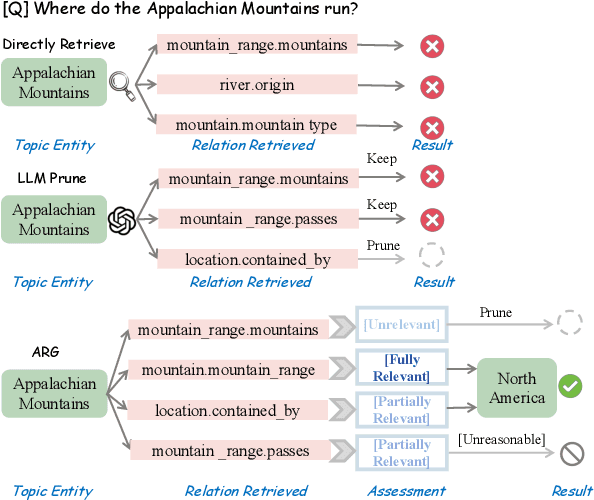
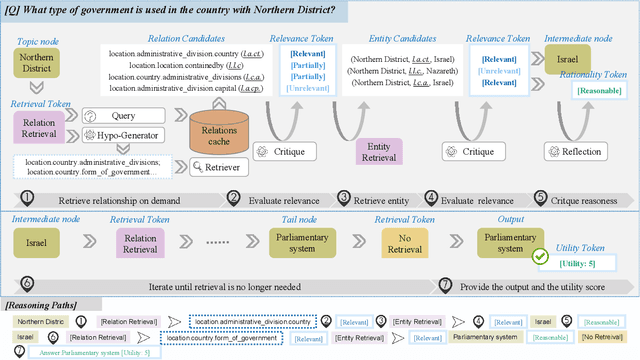
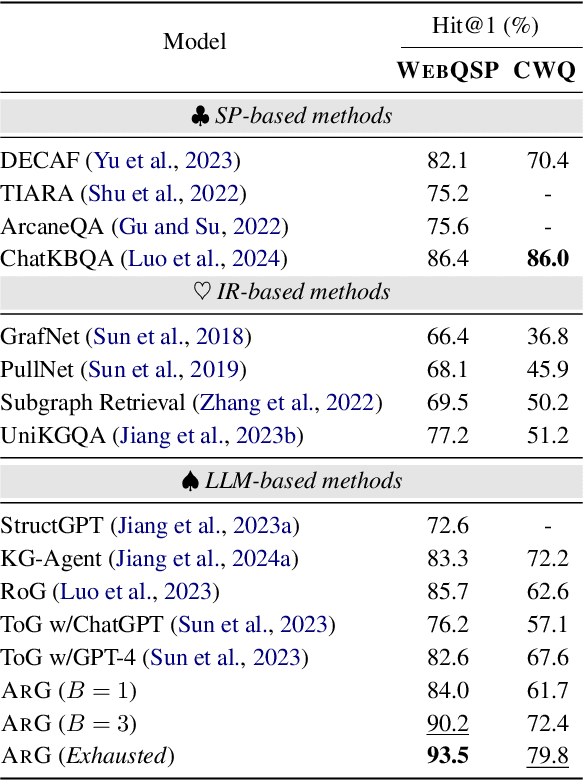
Extensive research has investigated the integration of large language models (LLMs) with knowledge graphs to enhance the reasoning process. However, understanding how models perform reasoning utilizing structured graph knowledge remains underexplored. Most existing approaches rely on LLMs or retrievers to make binary judgments regarding the utilization of knowledge, which is too coarse. Meanwhile, there is still a lack of feedback mechanisms for reflection and correction throughout the entire reasoning path. This paper proposes an Active self-Reflection framework for knowledge Graph reasoning ARG, introducing for the first time an end-to-end training approach to achieve iterative reasoning grounded on structured graphs. Within the framework, the model leverages special tokens to \textit{actively} determine whether knowledge retrieval is necessary, performs \textit{reflective} critique based on the retrieved knowledge, and iteratively reasons over the knowledge graph. The reasoning paths generated by the model exhibit high interpretability, enabling deeper exploration of the model's understanding of structured knowledge. Ultimately, the proposed model achieves outstanding results compared to existing baselines in knowledge graph reasoning tasks.

A Bayesian Mixture Model of Temporal Point Processes with Determinantal Point Process Prior

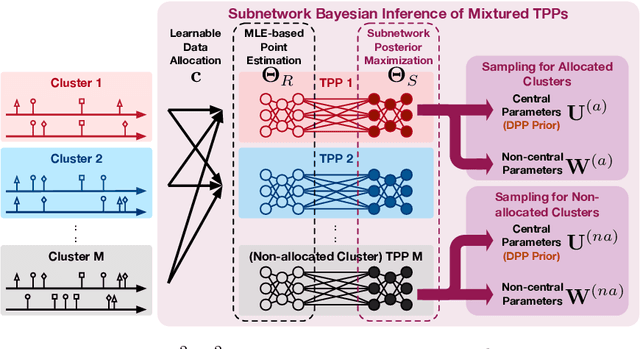
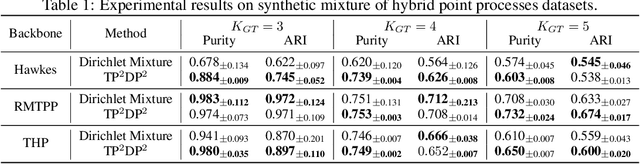
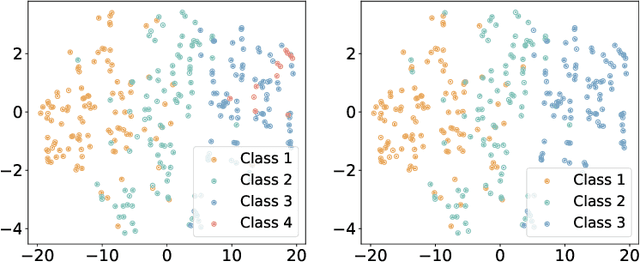
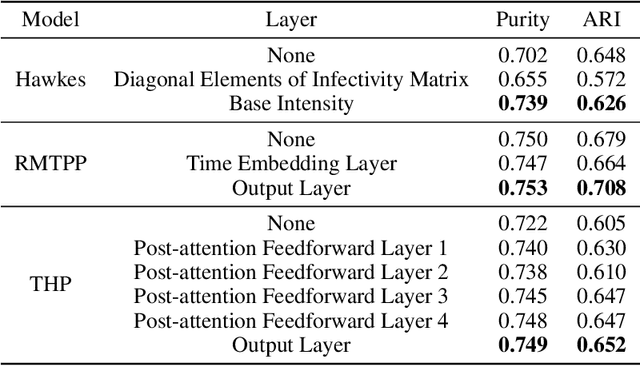
Asynchronous event sequence clustering aims to group similar event sequences in an unsupervised manner. Mixture models of temporal point processes have been proposed to solve this problem, but they often suffer from overfitting, leading to excessive cluster generation with a lack of diversity. To overcome these limitations, we propose a Bayesian mixture model of Temporal Point Processes with Determinantal Point Process prior (TP$^2$DP$^2$) and accordingly an efficient posterior inference algorithm based on conditional Gibbs sampling. Our work provides a flexible learning framework for event sequence clustering, enabling automatic identification of the potential number of clusters and accurate grouping of sequences with similar features. It is applicable to a wide range of parametric temporal point processes, including neural network-based models. Experimental results on both synthetic and real-world data suggest that our framework could produce moderately fewer yet more diverse mixture components, and achieve outstanding results across multiple evaluation metrics.

Pedestrian Volume Prediction Using a Diffusion Convolutional Gated Recurrent Unit Model

Effective models for analysing and predicting pedestrian flow are important to ensure the safety of both pedestrians and other road users. These tools also play a key role in optimising infrastructure design and geometry and supporting the economic utility of interconnected communities. The implementation of city-wide automatic pedestrian counting systems provides researchers with invaluable data, enabling the development and training of deep learning applications that offer better insights into traffic and crowd flows. Benefiting from real-world data provided by the City of Melbourne pedestrian counting system, this study presents a pedestrian flow prediction model, as an extension of Diffusion Convolutional Grated Recurrent Unit (DCGRU) with dynamic time warping, named DCGRU-DTW. This model captures the spatial dependencies of pedestrian flow through the diffusion process and the temporal dependency captured by Gated Recurrent Unit (GRU). Through extensive numerical experiments, we demonstrate that the proposed model outperforms the classic vector autoregressive model and the original DCGRU across multiple model accuracy metrics.

Better Locally Private Sparse Estimation Given Multiple Samples Per User

Previous studies yielded discouraging results for item-level locally differentially private linear regression with $s^*$-sparsity assumption, where the minimax rate for $nm$ samples is $\mathcal{O}(s^{*}d / nm\varepsilon^2)$. This can be challenging for high-dimensional data, where the dimension $d$ is extremely large. In this work, we investigate user-level locally differentially private sparse linear regression. We show that with $n$ users each contributing $m$ samples, the linear dependency of dimension $d$ can be eliminated, yielding an error upper bound of $\mathcal{O}(s^{*2} / nm\varepsilon^2)$. We propose a framework that first selects candidate variables and then conducts estimation in the narrowed low-dimensional space, which is extendable to general sparse estimation problems with tight error bounds. Experiments on both synthetic and real datasets demonstrate the superiority of the proposed methods. Both the theoretical and empirical results suggest that, with the same number of samples, locally private sparse estimation is better conducted when multiple samples per user are available.

ALTER: Augmentation for Large-Table-Based Reasoning

While extensive research has explored the use of large language models (LLMs) for table-based reasoning, most approaches struggle with scalability when applied to large tables. To maintain the superior comprehension abilities of LLMs in these scenarios, we introduce ALTER(Augmentation for Large-Table-Based Reasoning)-a framework designed to harness the latent augmentation potential in both free-form natural language (NL) questions, via the query augmentor, and semi-structured tabular data, through the table augmentor. By utilizing only a small subset of relevant data from the table and supplementing it with pre-augmented schema, semantic, and literal information, ALTER achieves outstanding performance on table-based reasoning benchmarks. We also provide a detailed analysis of large-table scenarios, comparing different methods and various partitioning principles. In these scenarios, our method outperforms all other approaches and exhibits robustness and efficiency against perturbations.

Locally Private Estimation with Public Features

We initiate the study of locally differentially private (LDP) learning with public features. We define semi-feature LDP, where some features are publicly available while the remaining ones, along with the label, require protection under local differential privacy. Under semi-feature LDP, we demonstrate that the mini-max convergence rate for non-parametric regression is significantly reduced compared to that of classical LDP. Then we propose HistOfTree, an estimator that fully leverages the information contained in both public and private features. Theoretically, HistOfTree reaches the mini-max optimal convergence rate. Empirically, HistOfTree achieves superior performance on both synthetic and real data. We also explore scenarios where users have the flexibility to select features for protection manually. In such cases, we propose an estimator and a data-driven parameter tuning strategy, leading to analogous theoretical and empirical results.

Bagged Regularized $k$-Distances for Anomaly Detection

We consider the paradigm of unsupervised anomaly detection, which involves the identification of anomalies within a dataset in the absence of labeled examples. Though distance-based methods are top-performing for unsupervised anomaly detection, they suffer heavily from the sensitivity to the choice of the number of the nearest neighbors. In this paper, we propose a new distance-based algorithm called bagged regularized $k$-distances for anomaly detection (BRDAD) converting the unsupervised anomaly detection problem into a convex optimization problem. Our BRDAD algorithm selects the weights by minimizing the surrogate risk, i.e., the finite sample bound of the empirical risk of the bagged weighted $k$-distances for density estimation (BWDDE). This approach enables us to successfully address the sensitivity challenge of the hyperparameter choice in distance-based algorithms. Moreover, when dealing with large-scale datasets, the efficiency issues can be addressed by the incorporated bagging technique in our BRDAD algorithm. On the theoretical side, we establish fast convergence rates of the AUC regret of our algorithm and demonstrate that the bagging technique significantly reduces the computational complexity. On the practical side, we conduct numerical experiments on anomaly detection benchmarks to illustrate the insensitivity of parameter selection of our algorithm compared with other state-of-the-art distance-based methods. Moreover, promising improvements are brought by applying the bagging technique in our algorithm on real-world datasets.

Optimal Locally Private Nonparametric Classification with Public Data

In this work, we investigate the problem of public data-assisted non-interactive LDP (Local Differential Privacy) learning with a focus on non-parametric classification. Under the posterior drift assumption, we for the first time derive the mini-max optimal convergence rate with LDP constraint. Then, we present a novel approach, the locally private classification tree, which attains the mini-max optimal convergence rate. Furthermore, we design a data-driven pruning procedure that avoids parameter tuning and produces a fast converging estimator. Comprehensive experiments conducted on synthetic and real datasets show the superior performance of our proposed method. Both our theoretical and experimental findings demonstrate the effectiveness of public data compared to private data, which leads to practical suggestions for prioritizing non-private data collection.

Augmented Abstractive Summarization With Document-LevelSemantic Graph

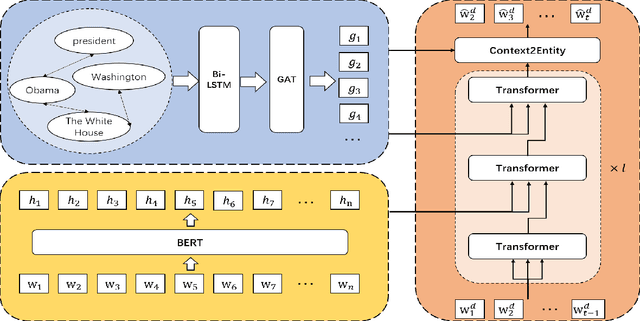
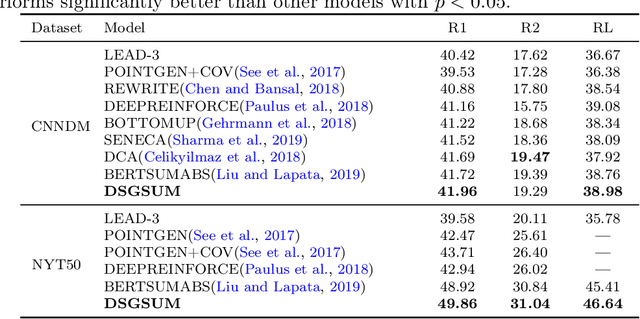
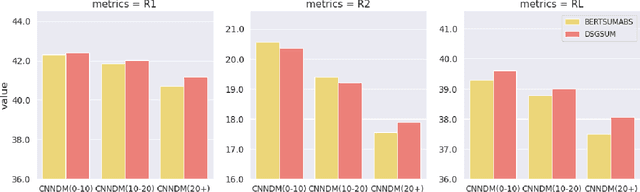
Previous abstractive methods apply sequence-to-sequence structures to generate summary without a module to assist the system to detect vital mentions and relationships within a document. To address this problem, we utilize semantic graph to boost the generation performance. Firstly, we extract important entities from each document and then establish a graph inspired by the idea of distant supervision \citep{mintz-etal-2009-distant}. Then, we combine a Bi-LSTM with a graph encoder to obtain the representation of each graph node. A novel neural decoder is presented to leverage the information of such entity graphs. Automatic and human evaluations show the effectiveness of our technique.