Time Series Treatment Effects Analysis with Always-Missing Controls

Estimating treatment effects in time series data presents a significant challenge, especially when the control group is always unobservable. For example, in analyzing the effects of Christmas on retail sales, we lack direct observation of what would have occurred in late December without the Christmas impact. To address this, we try to recover the control group in the event period while accounting for confounders and temporal dependencies. Experimental results on the M5 Walmart retail sales data demonstrate robust estimation of the potential outcome of the control group as well as accurate predicted holiday effect. Furthermore, we provided theoretical guarantees for the estimated treatment effect, proving its consistency and asymptotic normality. The proposed methodology is applicable not only to this always-missing control scenario but also in other conventional time series causal inference settings.

A Bayesian Mixture Model of Temporal Point Processes with Determinantal Point Process Prior

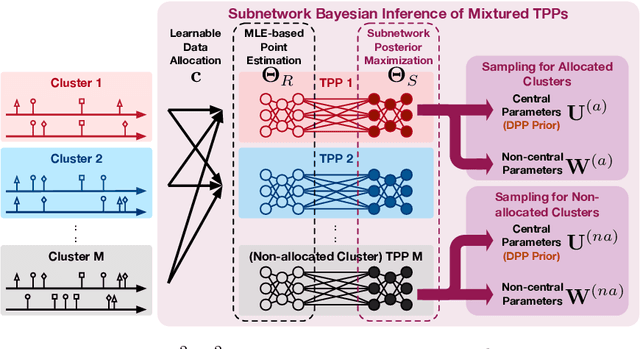
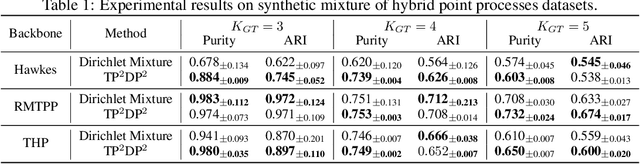
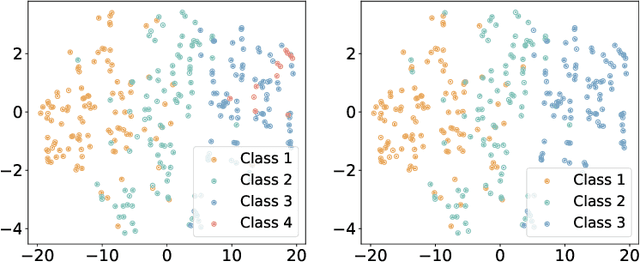
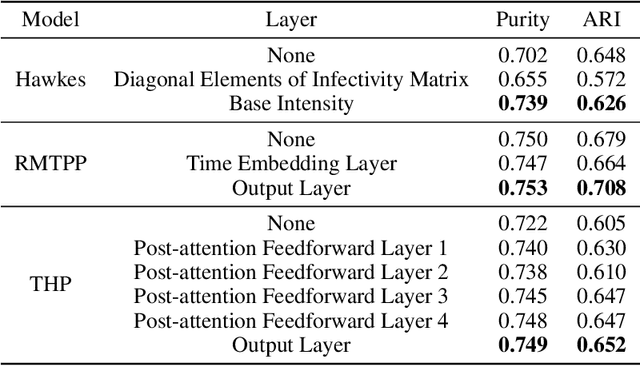
Asynchronous event sequence clustering aims to group similar event sequences in an unsupervised manner. Mixture models of temporal point processes have been proposed to solve this problem, but they often suffer from overfitting, leading to excessive cluster generation with a lack of diversity. To overcome these limitations, we propose a Bayesian mixture model of Temporal Point Processes with Determinantal Point Process prior (TP$^2$DP$^2$) and accordingly an efficient posterior inference algorithm based on conditional Gibbs sampling. Our work provides a flexible learning framework for event sequence clustering, enabling automatic identification of the potential number of clusters and accurate grouping of sequences with similar features. It is applicable to a wide range of parametric temporal point processes, including neural network-based models. Experimental results on both synthetic and real-world data suggest that our framework could produce moderately fewer yet more diverse mixture components, and achieve outstanding results across multiple evaluation metrics.

Online Statistical Inference for Matrix Contextual Bandit

Contextual bandit has been widely used for sequential decision-making based on the current contextual information and historical feedback data. In modern applications, such context format can be rich and can often be formulated as a matrix. Moreover, while existing bandit algorithms mainly focused on reward-maximization, less attention has been paid to the statistical inference. To fill in these gaps, in this work we consider a matrix contextual bandit framework where the true model parameter is a low-rank matrix, and propose a fully online procedure to simultaneously make sequential decision-making and conduct statistical inference. The low-rank structure of the model parameter and the adaptivity nature of the data collection process makes this difficult: standard low-rank estimators are not fully online and are biased, while existing inference approaches in bandit algorithms fail to account for the low-rankness and are also biased. To address these, we introduce a new online doubly-debiasing inference procedure to simultaneously handle both sources of bias. In theory, we establish the asymptotic normality of the proposed online doubly-debiased estimator and prove the validity of the constructed confidence interval. Our inference results are built upon a newly developed low-rank stochastic gradient descent estimator and its non-asymptotic convergence result, which is also of independent interest.