A Bayesian Mixture Model of Temporal Point Processes with Determinantal Point Process Prior

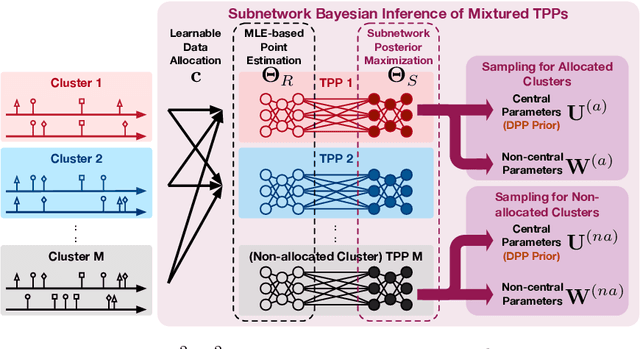
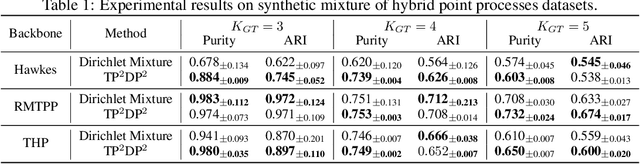
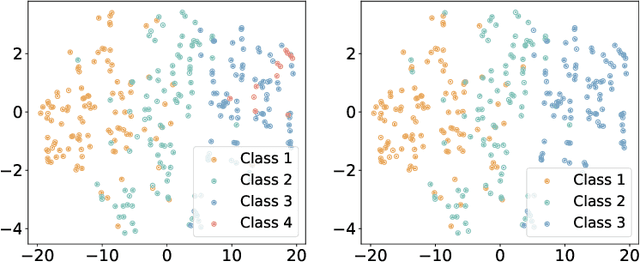
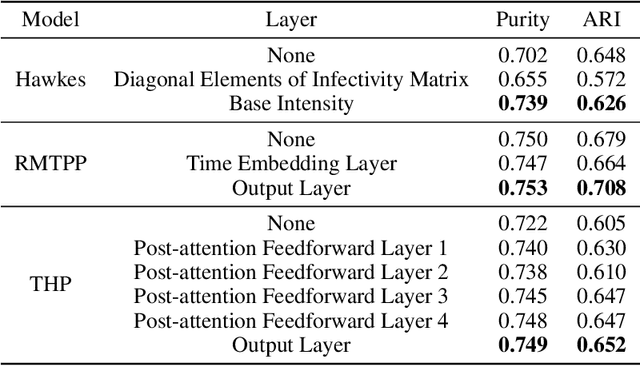
Asynchronous event sequence clustering aims to group similar event sequences in an unsupervised manner. Mixture models of temporal point processes have been proposed to solve this problem, but they often suffer from overfitting, leading to excessive cluster generation with a lack of diversity. To overcome these limitations, we propose a Bayesian mixture model of Temporal Point Processes with Determinantal Point Process prior (TP$^2$DP$^2$) and accordingly an efficient posterior inference algorithm based on conditional Gibbs sampling. Our work provides a flexible learning framework for event sequence clustering, enabling automatic identification of the potential number of clusters and accurate grouping of sequences with similar features. It is applicable to a wide range of parametric temporal point processes, including neural network-based models. Experimental results on both synthetic and real-world data suggest that our framework could produce moderately fewer yet more diverse mixture components, and achieve outstanding results across multiple evaluation metrics.

Pedestrian Volume Prediction Using a Diffusion Convolutional Gated Recurrent Unit Model

Effective models for analysing and predicting pedestrian flow are important to ensure the safety of both pedestrians and other road users. These tools also play a key role in optimising infrastructure design and geometry and supporting the economic utility of interconnected communities. The implementation of city-wide automatic pedestrian counting systems provides researchers with invaluable data, enabling the development and training of deep learning applications that offer better insights into traffic and crowd flows. Benefiting from real-world data provided by the City of Melbourne pedestrian counting system, this study presents a pedestrian flow prediction model, as an extension of Diffusion Convolutional Grated Recurrent Unit (DCGRU) with dynamic time warping, named DCGRU-DTW. This model captures the spatial dependencies of pedestrian flow through the diffusion process and the temporal dependency captured by Gated Recurrent Unit (GRU). Through extensive numerical experiments, we demonstrate that the proposed model outperforms the classic vector autoregressive model and the original DCGRU across multiple model accuracy metrics.