GAD-NR: Graph Anomaly Detection via Neighborhood Reconstruction

Graph Anomaly Detection (GAD) is a technique used to identify abnormal nodes within graphs, finding applications in network security, fraud detection, social media spam detection, and various other domains. A common method for GAD is Graph Auto-Encoders (GAEs), which encode graph data into node representations and identify anomalies by assessing the reconstruction quality of the graphs based on these representations. However, existing GAE models are primarily optimized for direct link reconstruction, resulting in nodes connected in the graph being clustered in the latent space. As a result, they excel at detecting cluster-type structural anomalies but struggle with more complex structural anomalies that do not conform to clusters. To address this limitation, we propose a novel solution called GAD-NR, a new variant of GAE that incorporates neighborhood reconstruction for graph anomaly detection. GAD-NR aims to reconstruct the entire neighborhood of a node, encompassing the local structure, self-attributes, and neighbor attributes, based on the corresponding node representation. By comparing the neighborhood reconstruction loss between anomalous nodes and normal nodes, GAD-NR can effectively detect any anomalies. Extensive experimentation conducted on six real-world datasets validates the effectiveness of GAD-NR, showcasing significant improvements (by up to 30% in AUC) over state-of-the-art competitors. The source code for GAD-NR is openly available. Importantly, the comparative analysis reveals that the existing methods perform well only in detecting one or two types of anomalies out of the three types studied. In contrast, GAD-NR excels at detecting all three types of anomalies across the datasets, demonstrating its comprehensive anomaly detection capabilities.

Contrastive Cycle Adversarial Autoencoders for Single-cell Multi-omics Alignment and Integration

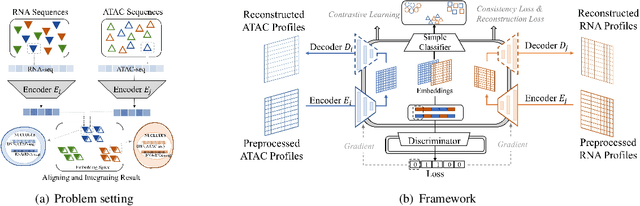
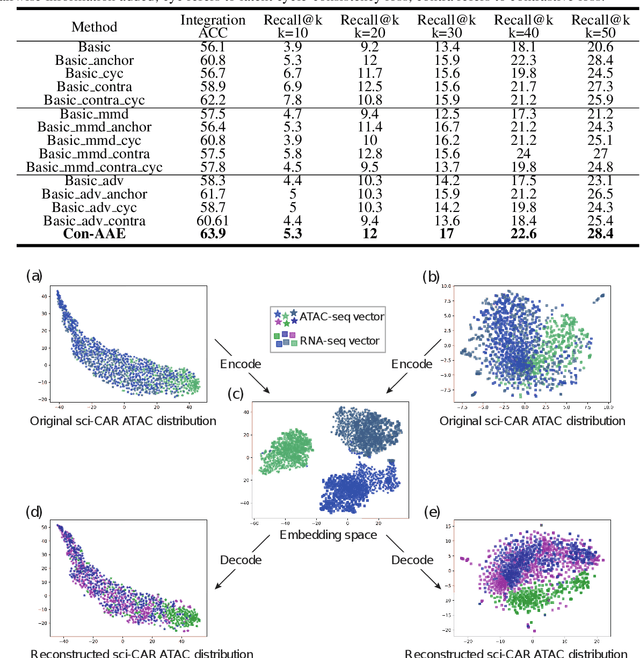
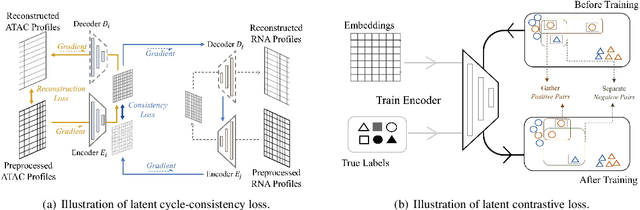
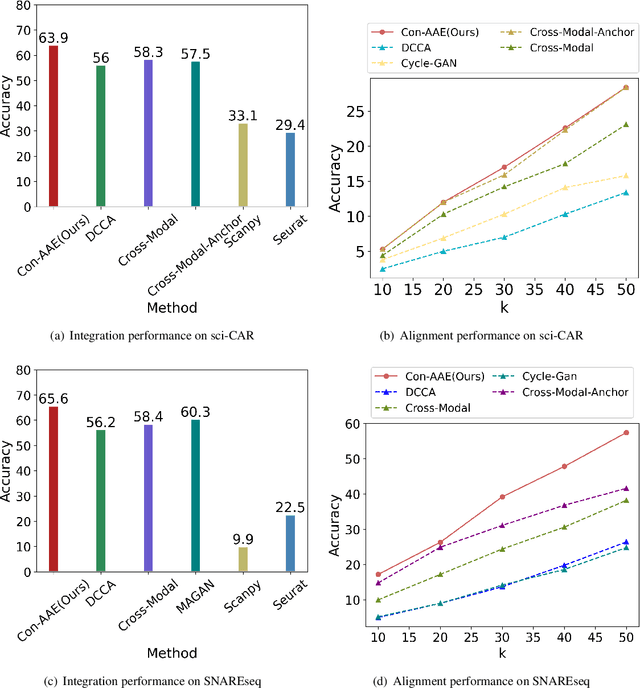
Muilti-modality data are ubiquitous in biology, especially that we have entered the multi-omics era, when we can measure the same biological object (cell) from different aspects (omics) to provide a more comprehensive insight into the cellular system. When dealing with such multi-omics data, the first step is to determine the correspondence among different modalities. In other words, we should match data from different spaces corresponding to the same object. This problem is particularly challenging in the single-cell multi-omics scenario because such data are very sparse with extremely high dimensions. Secondly, matched single-cell multi-omics data are rare and hard to collect. Furthermore, due to the limitations of the experimental environment, the data are usually highly noisy. To promote the single-cell multi-omics research, we overcome the above challenges, proposing a novel framework to align and integrate single-cell RNA-seq data and single-cell ATAC-seq data. Our approach can efficiently map the above data with high sparsity and noise from different spaces to a low-dimensional manifold in a unified space, making the downstream alignment and integration straightforward. Compared with the other state-of-the-art methods, our method performs better in both simulated and real single-cell data. The proposed method is helpful for the single-cell multi-omics research. The improvement for integration on the simulated data is significant.

Understanding Adversarial Examples Through Deep Neural Network's Response Surface and Uncertainty Regions

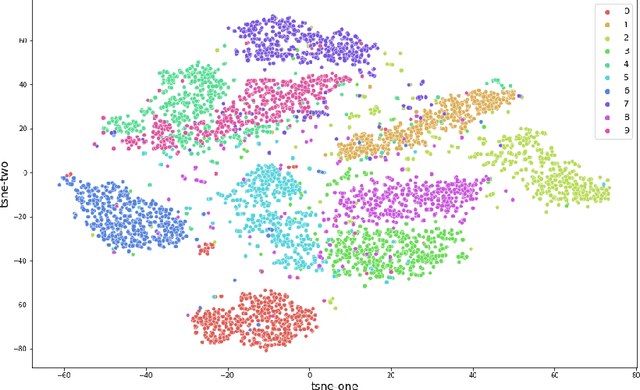
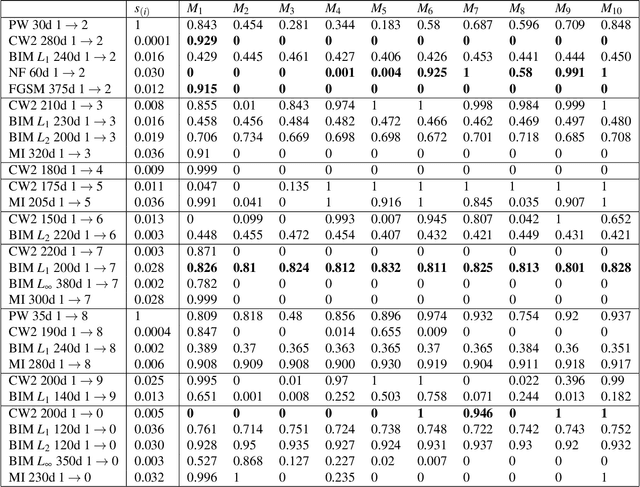
Deep neural network (DNN) is a popular model implemented in many systems to handle complex tasks such as image classification, object recognition, natural language processing etc. Consequently DNN structural vulnerabilities become part of the security vulnerabilities in those systems. In this paper we study the root cause of DNN adversarial examples. We examine the DNN response surface to understand its classification boundary. Our study reveals the structural problem of DNN classification boundary that leads to the adversarial examples. Existing attack algorithms can generate from a handful to a few hundred adversarial examples given one clean image. We show there are infinitely many adversarial images given one clean sample, all within a small neighborhood of the clean sample. We then define DNN uncertainty regions and show transferability of adversarial examples is not universal. We also argue that generalization error, the large sample theoretical guarantee established for DNN, cannot adequately capture the phenomenon of adversarial examples. We need new theory to measure DNN robustness.