Linhao Song
Nonlinear functional regression by functional deep neural network with kernel embedding
Jan 05, 2024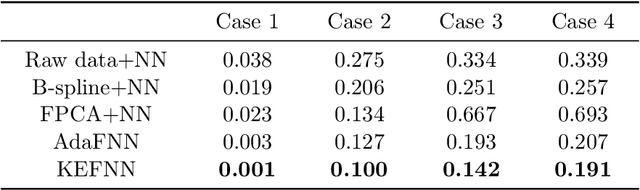
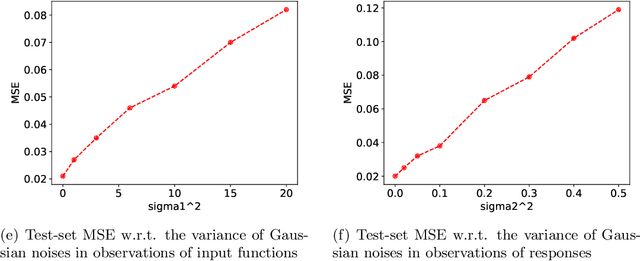

Abstract:With the rapid development of deep learning in various fields of science and technology, such as speech recognition, image classification, and natural language processing, recently it is also widely applied in the functional data analysis (FDA) with some empirical success. However, due to the infinite dimensional input, we need a powerful dimension reduction method for functional learning tasks, especially for the nonlinear functional regression. In this paper, based on the idea of smooth kernel integral transformation, we propose a functional deep neural network with an efficient and fully data-dependent dimension reduction method. The architecture of our functional net consists of a kernel embedding step: an integral transformation with a data-dependent smooth kernel; a projection step: a dimension reduction by projection with eigenfunction basis based on the embedding kernel; and finally an expressive deep ReLU neural network for the prediction. The utilization of smooth kernel embedding enables our functional net to be discretization invariant, efficient, and robust to noisy observations, capable of utilizing information in both input functions and responses data, and have a low requirement on the number of discrete points for an unimpaired generalization performance. We conduct theoretical analysis including approximation error and generalization error analysis, and numerical simulations to verify these advantages of our functional net.
Approximation of Nonlinear Functionals Using Deep ReLU Networks
Apr 10, 2023Abstract:In recent years, functional neural networks have been proposed and studied in order to approximate nonlinear continuous functionals defined on $L^p([-1, 1]^s)$ for integers $s\ge1$ and $1\le p<\infty$. However, their theoretical properties are largely unknown beyond universality of approximation or the existing analysis does not apply to the rectified linear unit (ReLU) activation function. To fill in this void, we investigate here the approximation power of functional deep neural networks associated with the ReLU activation function by constructing a continuous piecewise linear interpolation under a simple triangulation. In addition, we establish rates of approximation of the proposed functional deep ReLU networks under mild regularity conditions. Finally, our study may also shed some light on the understanding of functional data learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge