Can overfitted deep neural networks in adversarial training generalize? -- An approximation viewpoint

Adversarial training is a widely used method to improve the robustness of deep neural networks (DNNs) over adversarial perturbations. However, it is empirically observed that adversarial training on over-parameterized networks often suffers from the \textit{robust overfitting}: it can achieve almost zero adversarial training error while the robust generalization performance is not promising. In this paper, we provide a theoretical understanding of the question of whether overfitted DNNs in adversarial training can generalize from an approximation viewpoint. Specifically, our main results are summarized into three folds: i) For classification, we prove by construction the existence of infinitely many adversarial training classifiers on over-parameterized DNNs that obtain arbitrarily small adversarial training error (overfitting), whereas achieving good robust generalization error under certain conditions concerning the data quality, well separated, and perturbation level. ii) Linear over-parameterization (meaning that the number of parameters is only slightly larger than the sample size) is enough to ensure such existence if the target function is smooth enough. iii) For regression, our results demonstrate that there also exist infinitely many overfitted DNNs with linear over-parameterization in adversarial training that can achieve almost optimal rates of convergence for the standard generalization error. Overall, our analysis points out that robust overfitting can be avoided but the required model capacity will depend on the smoothness of the target function, while a robust generalization gap is inevitable. We hope our analysis will give a better understanding of the mathematical foundations of robustness in DNNs from an approximation view.

Nonlinear functional regression by functional deep neural network with kernel embedding

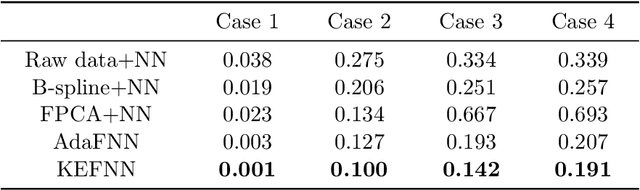
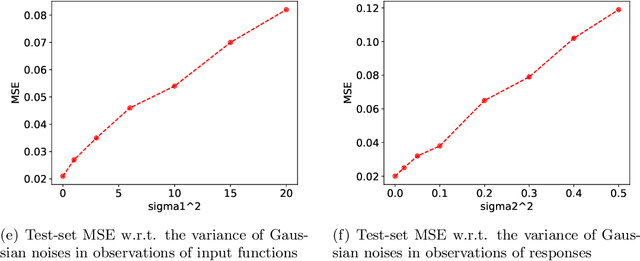
With the rapid development of deep learning in various fields of science and technology, such as speech recognition, image classification, and natural language processing, recently it is also widely applied in the functional data analysis (FDA) with some empirical success. However, due to the infinite dimensional input, we need a powerful dimension reduction method for functional learning tasks, especially for the nonlinear functional regression. In this paper, based on the idea of smooth kernel integral transformation, we propose a functional deep neural network with an efficient and fully data-dependent dimension reduction method. The architecture of our functional net consists of a kernel embedding step: an integral transformation with a data-dependent smooth kernel; a projection step: a dimension reduction by projection with eigenfunction basis based on the embedding kernel; and finally an expressive deep ReLU neural network for the prediction. The utilization of smooth kernel embedding enables our functional net to be discretization invariant, efficient, and robust to noisy observations, capable of utilizing information in both input functions and responses data, and have a low requirement on the number of discrete points for an unimpaired generalization performance. We conduct theoretical analysis including approximation error and generalization error analysis, and numerical simulations to verify these advantages of our functional net.

Learning Theory of Distribution Regression with Neural Networks

In this paper, we aim at establishing an approximation theory and a learning theory of distribution regression via a fully connected neural network (FNN). In contrast to the classical regression methods, the input variables of distribution regression are probability measures. Then we often need to perform a second-stage sampling process to approximate the actual information of the distribution. On the other hand, the classical neural network structure requires the input variable to be a vector. When the input samples are probability distributions, the traditional deep neural network method cannot be directly used and the difficulty arises for distribution regression. A well-defined neural network structure for distribution inputs is intensively desirable. There is no mathematical model and theoretical analysis on neural network realization of distribution regression. To overcome technical difficulties and address this issue, we establish a novel fully connected neural network framework to realize an approximation theory of functionals defined on the space of Borel probability measures. Furthermore, based on the established functional approximation results, in the hypothesis space induced by the novel FNN structure with distribution inputs, almost optimal learning rates for the proposed distribution regression model up to logarithmic terms are derived via a novel two-stage error decomposition technique.

Theory of Deep Convolutional Neural Networks III: Approximating Radial Functions

We consider a family of deep neural networks consisting of two groups of convolutional layers, a downsampling operator, and a fully connected layer. The network structure depends on two structural parameters which determine the numbers of convolutional layers and the width of the fully connected layer. We establish an approximation theory with explicit approximation rates when the approximated function takes a composite form $f\circ Q$ with a feature polynomial $Q$ and a univariate function $f$. In particular, we prove that such a network can outperform fully connected shallow networks in approximating radial functions with $Q(x) =|x|^2$, when the dimension $d$ of data from $\mathbb{R}^d$ is large. This gives the first rigorous proof for the superiority of deep convolutional neural networks in approximating functions with special structures. Then we carry out generalization analysis for empirical risk minimization with such a deep network in a regression framework with the regression function of the form $f\circ Q$. Our network structure which does not use any composite information or the functions $Q$ and $f$ can automatically extract features and make use of the composite nature of the regression function via tuning the structural parameters. Our analysis provides an error bound which decreases with the network depth to a minimum and then increases, verifying theoretically a trade-off phenomenon observed for network depths in many practical applications.