Latent Space Exploration Using Generative Kernel PCA

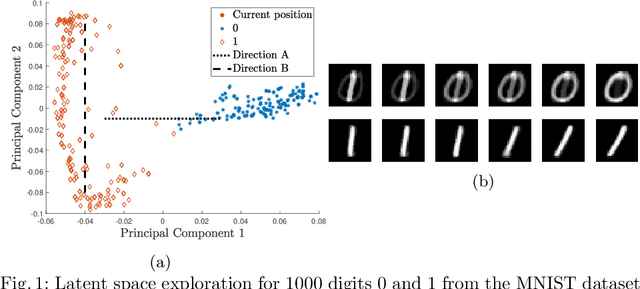
Kernel PCA is a powerful feature extractor which recently has seen a reformulation in the context of Restricted Kernel Machines (RKMs). These RKMs allow for a representation of kernel PCA in terms of hidden and visible units similar to Restricted Boltzmann Machines. This connection has led to insights on how to use kernel PCA in a generative procedure, called generative kernel PCA. In this paper, the use of generative kernel PCA for exploring latent spaces of datasets is investigated. New points can be generated by gradually moving in the latent space, which allows for an interpretation of the components. Firstly, examples of this feature space exploration on three datasets are shown with one of them leading to an interpretable representation of ECG signals. Afterwards, the use of the tool in combination with novelty detection is shown, where the latent space around novel patterns in the data is explored. This helps in the interpretation of why certain points are considered as novel.

Towards Deterministic Diverse Subset Sampling

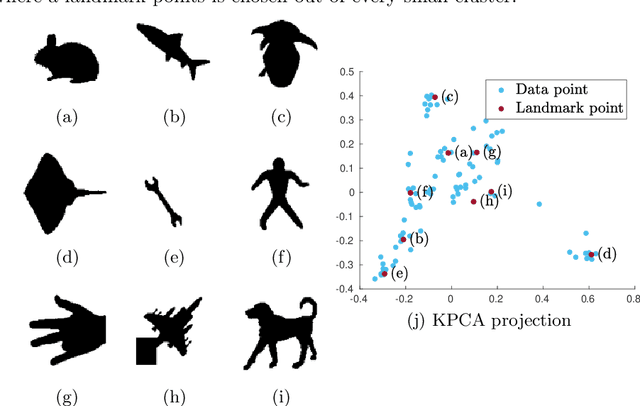
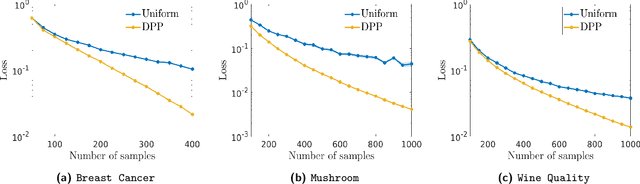
Determinantal point processes (DPPs) are well known models for diverse subset selection problems, including recommendation tasks, document summarization and image search. In this paper, we discuss a greedy deterministic adaptation of k-DPP. Deterministic algorithms are interesting for many applications, as they provide interpretability to the user by having no failure probability and always returning the same results. First, the ability of the method to yield low-rank approximations of kernel matrices is evaluated by comparing the accuracy of the Nystr\"om approximation on multiple datasets. Afterwards, we demonstrate the usefulness of the model on an image search task.

Leverage Score Sampling for Complete Mode Coverage in Generative Adversarial Networks

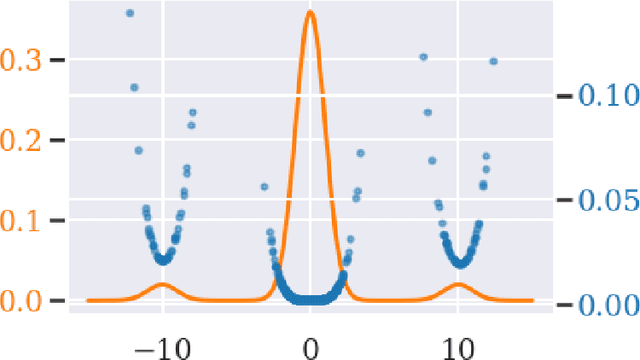
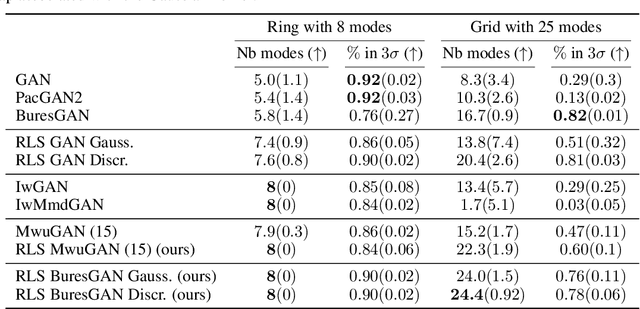
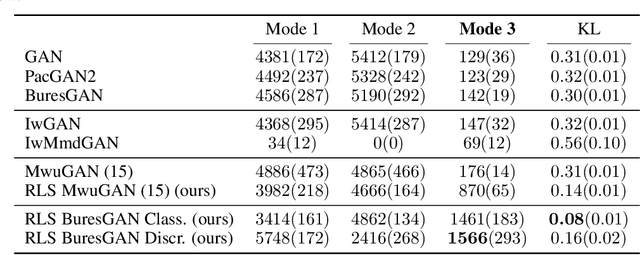
Commonly, machine learning models minimize an empirical expectation. As a result, the trained models typically perform well for the majority of the data but the performance may deteriorate on less dense regions of the dataset. This issue also arises in generative modeling. A generative model may overlook underrepresented modes that are less frequent in the empirical data distribution. This problem is known as complete mode coverage. We propose a sampling procedure based on ridge leverage scores which significantly improves mode coverage when compared to standard methods and can easily be combined with any GAN. Ridge Leverage Scores (RLSs) are computed by using an explicit feature map, associated with the next-to-last layer of a GAN discriminator or of a pre-trained network, or by using an implicit feature map corresponding to a Gaussian kernel. Multiple evaluations against recent approaches of complete mode coverage show a clear improvement when using the proposed sampling strategy.

Determinantal Point Processes Implicitly Regularize Semi-parametric Regression Problems

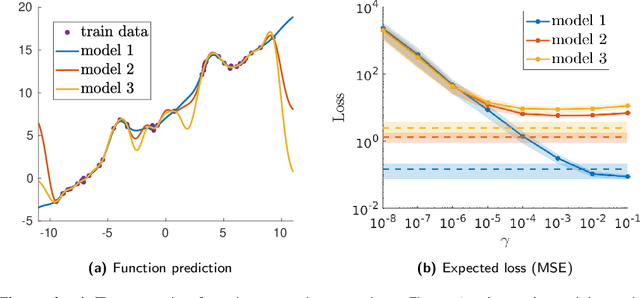
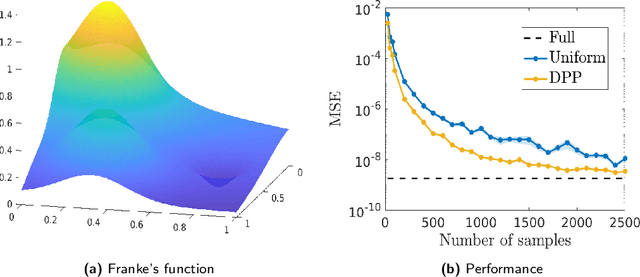
Semi-parametric regression models are used in several applications which require comprehensibility without sacrificing accuracy. Examples are spline interpolation in geophysics, or non-linear time series problems, where the system includes for instance a linear and non-linear component. We discuss here the use of a finite Determinantal Point Process (DPP) sampling for approximating semi-parametric models in two cases. On the one hand, in the case of large training data sets, DPP sampling is used to reduce the number of model parameters. On the other hand, DPPs can determine experimental designs in the case of the optimal interpolation models. Recently, Barthelm\'e, Tremblay, Usevich, and Amblard introduced a novel representation of finite DPP's. They formulated extended $L$-ensembles that can conveniently represent for instance partial-projection DPPs and suggest their use for optimal interpolation. With the help of this formalism, we derive a key identity illustrating the implicit regularization effect of determinantal sampling for semi-parametric regression and interpolation. Also, a novel projected Nystr\"om approximation is defined and used to derive a bound on the expected risk for the corresponding approximation of semi-parametric regression. This work naturally extends similar results obtained for kernel ridge regression.

Outlier detection in non-elliptical data by kernel MRCD

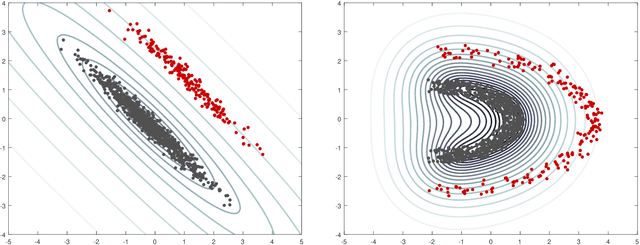
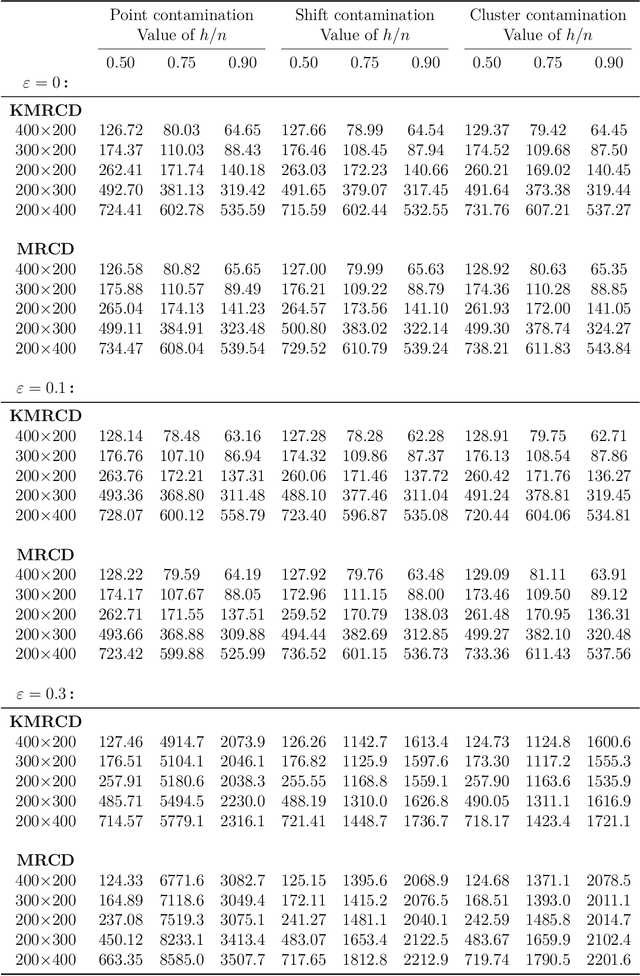
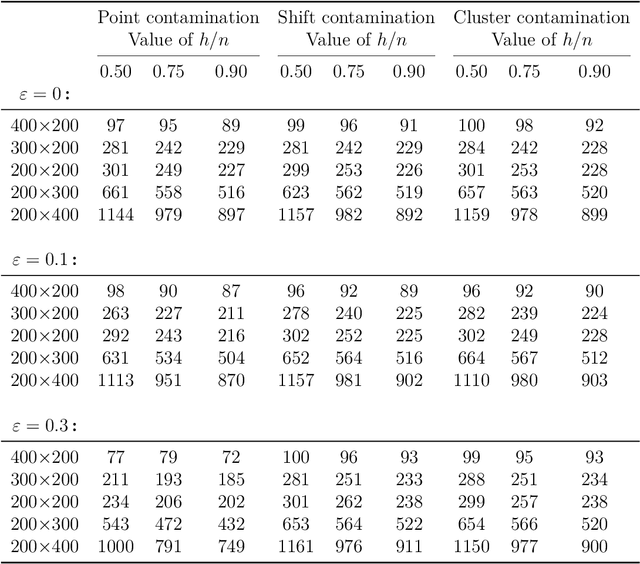
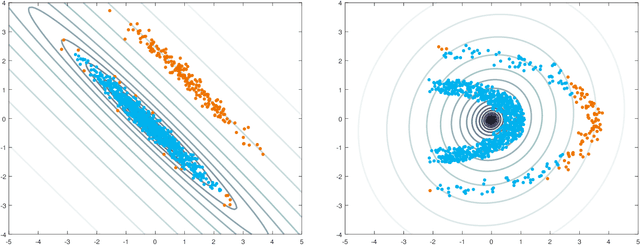
The minimum regularized covariance determinant method (MRCD) is a robust estimator for multivariate location and scatter, which detects outliers by fitting a robust covariance matrix to the data. Its regularization ensures that the covariance matrix is well-conditioned in any dimension. The MRCD assumes that the non-outlying observations are roughly elliptically distributed, but many datasets are not of that form. Moreover, the computation time of MRCD increases substantially when the number of variables goes up, and nowadays datasets with many variables are common. The proposed Kernel Minimum Regularized Covariance Determinant (KMRCD) estimator addresses both issues. It is not restricted to elliptical data because it implicitly computes the MRCD estimates in a kernel induced feature space. A fast algorithm is constructed that starts from kernel-based initial estimates and exploits the kernel trick to speed up the subsequent computations. Based on the KMRCD estimates, a rule is proposed to flag outliers. The KMRCD algorithm performs well in simulations, and is illustrated on real-life data.

Ensemble Kernel Methods, Implicit Regularization and Determinantal Point Processes

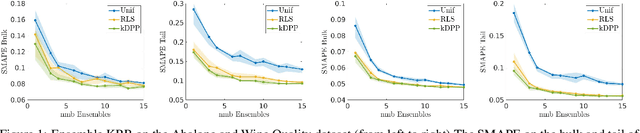
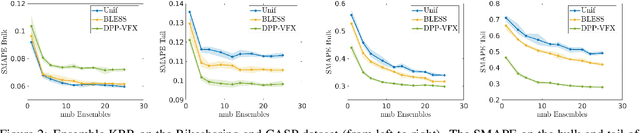
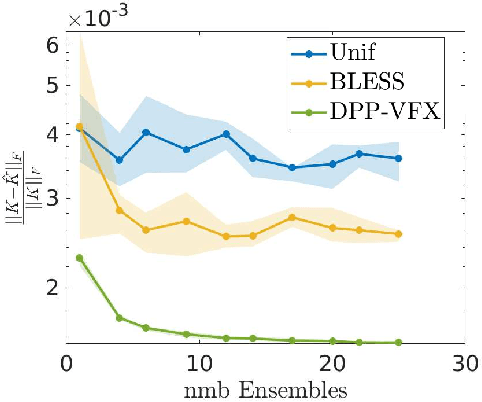
By using the framework of Determinantal Point Processes (DPPs), some theoretical results concerning the interplay between diversity and regularization can be obtained. In this paper we show that sampling subsets with kDPPs results in implicit regularization in the context of ridgeless Kernel Regression. Furthermore, we leverage the common setup of state-of-the-art DPP algorithms to sample multiple small subsets and use them in an ensemble of ridgeless regressions. Our first empirical results indicate that ensemble of ridgeless regressors can be interesting to use for datasets including redundant information.

The Bures Metric for Taming Mode Collapse in Generative Adversarial Networks

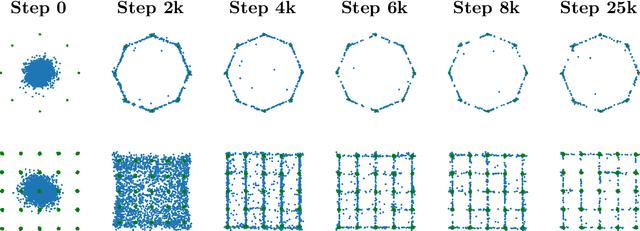
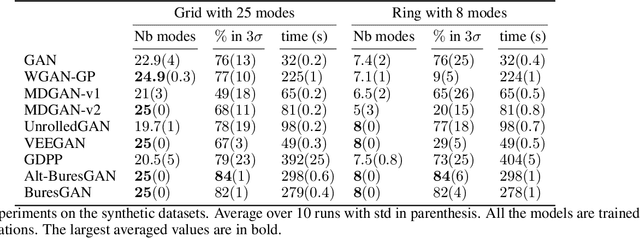
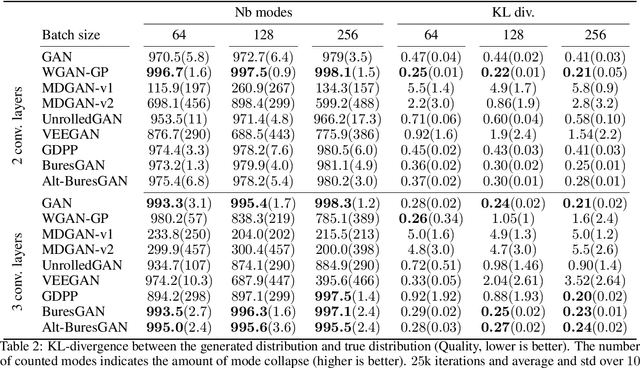
Generative Adversarial Networks (GANs) are performant generative methods yielding high-quality samples. However, under certain circumstances, the training of GANs can lead to mode collapse or mode dropping, i.e. the generative models not being able to sample from the entire probability distribution. To address this problem, we use the last layer of the discriminator as a feature map to study the distribution of the real and the fake data. During training, we propose to match the real batch diversity to the fake batch diversity by using the Bures distance between covariance matrices in feature space. The computation of the Bures distance can be conveniently done in either feature space or kernel space in terms of the covariance and kernel matrix respectively. We observe that diversity matching reduces mode collapse substantially and has a positive effect on the sample quality. On the practical side, a very simple training procedure, that does not require additional hyperparameter tuning, is proposed and assessed on several datasets.

Disentangled Representation Learning and Generation with Manifold Optimization

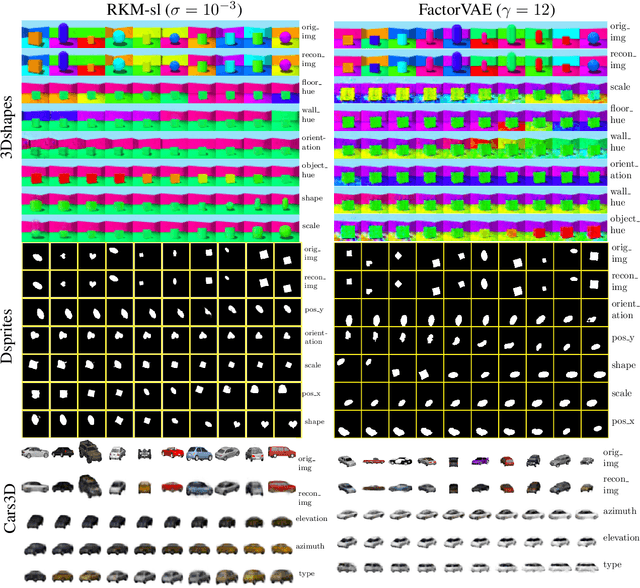
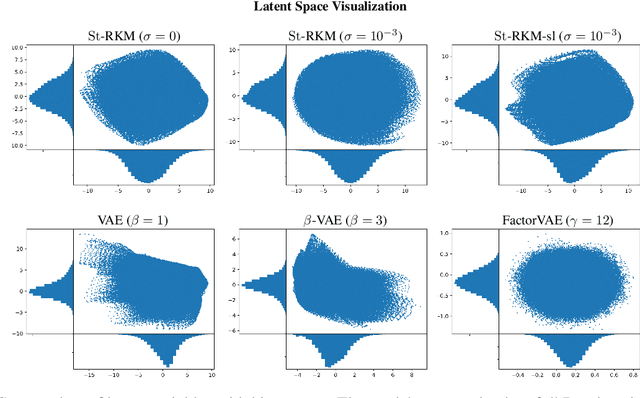
Disentanglement is an enjoyable property in representation learning which increases the interpretability of generative models such as Variational Auto-Encoders (VAE), Generative Adversarial Models and their many variants. In the context of latent space models, this work presents a representation learning framework that explicitly promotes disentanglement thanks to the combination of an auto-encoder with Principal Component Analysis (PCA) in latent space. The proposed objective is the sum of an auto-encoder error term along with a PCA reconstruction error in the feature space. This has an interpretation of a Restricted Kernel Machine with an interconnection matrix on the Stiefel manifold. The construction encourages a matching between the principal directions in latent space and the directions of orthogonal variation in data space. The training algorithm involves a stochastic optimization method on the Stiefel manifold, which increases only marginally the computing time compared to an analogous VAE. Our theoretical discussion and various experiments show that the proposed model improves over many VAE variants along with special emphasis on disentanglement learning.

Diversity sampling is an implicit regularization for kernel methods

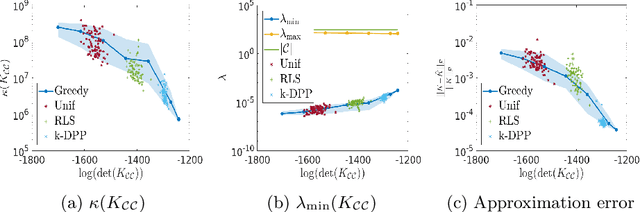
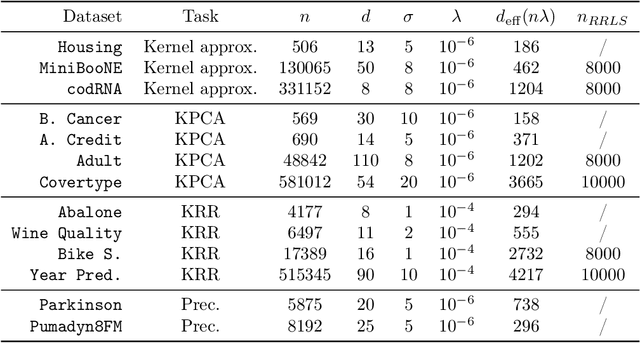
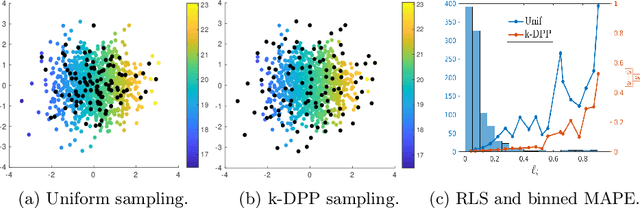
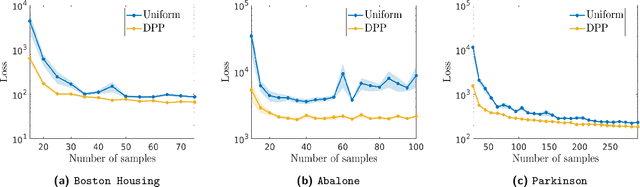
Kernel methods have achieved very good performance on large scale regression and classification problems, by using the Nystr\"om method and preconditioning techniques. The Nystr\"om approximation -- based on a subset of landmarks -- gives a low rank approximation of the kernel matrix, and is known to provide a form of implicit regularization. We further elaborate on the impact of sampling diverse landmarks for constructing the Nystr\"om approximation in supervised as well as unsupervised kernel methods. By using Determinantal Point Processes for sampling, we obtain additional theoretical results concerning the interplay between diversity and regularization. Empirically, we demonstrate the advantages of training kernel methods based on subsets made of diverse points. In particular, if the dataset has a dense bulk and a sparser tail, we show that Nystr\"om kernel regression with diverse landmarks increases the accuracy of the regression in sparser regions of the dataset, with respect to a uniform landmark sampling. A greedy heuristic is also proposed to select diverse samples of significant size within large datasets when exact DPP sampling is not practically feasible.

Robust Generative Restricted Kernel Machines using Weighted Conjugate Feature Duality

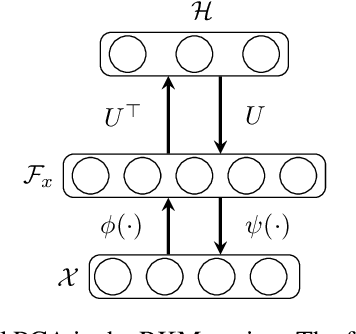
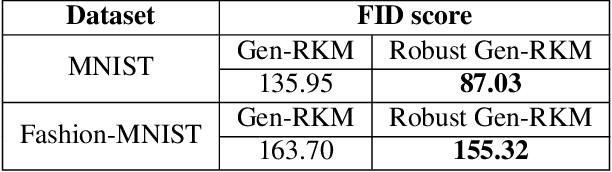
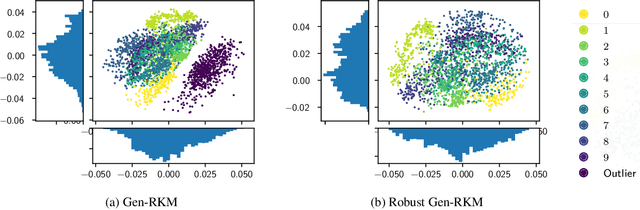
In the past decade, interest in generative models has grown tremendously. However, their training performance can be highly affected by contamination, where outliers are encoded in the representation of the model. This results in the generation of noisy data. In this paper, we introduce a weighted conjugate feature duality in the framework of Restricted Kernel Machines (RKMs). This formulation is used to fine-tune the latent space of generative RKMs using a weighting function based on the Minimum Covariance Determinant, which is a highly robust estimator of multivariate location and scatter. Experiments show that the weighted RKM is capable of generating clean images when contamination is present in the training data. We further show that the robust method also preserves uncorrelated feature learning through qualitative and quantitative experiments on standard datasets.