Outlier detection in non-elliptical data by kernel MRCD
Paper and Code
Aug 05, 2020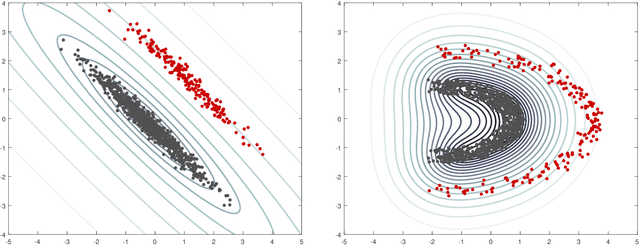
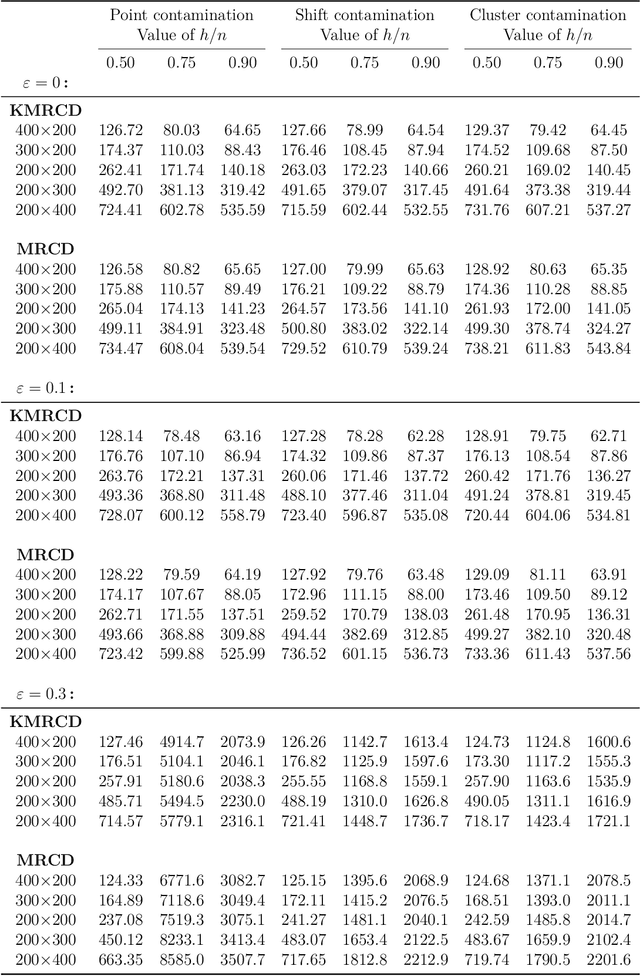
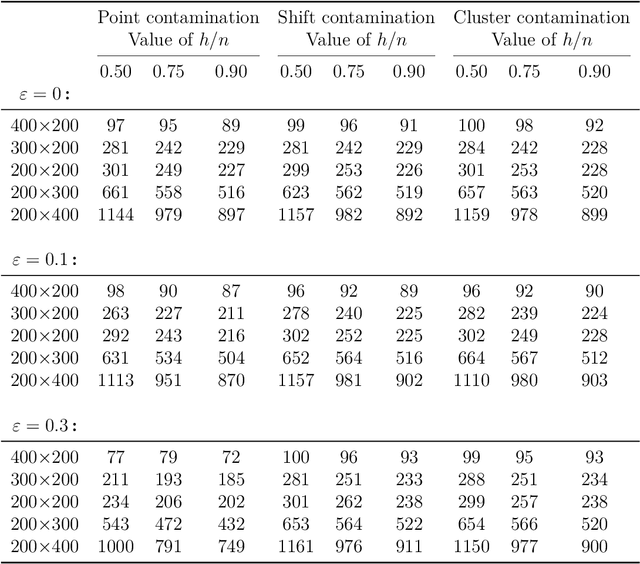
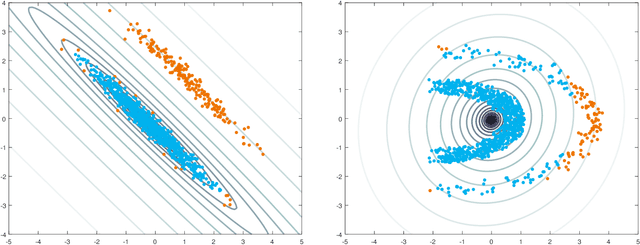
The minimum regularized covariance determinant method (MRCD) is a robust estimator for multivariate location and scatter, which detects outliers by fitting a robust covariance matrix to the data. Its regularization ensures that the covariance matrix is well-conditioned in any dimension. The MRCD assumes that the non-outlying observations are roughly elliptically distributed, but many datasets are not of that form. Moreover, the computation time of MRCD increases substantially when the number of variables goes up, and nowadays datasets with many variables are common. The proposed Kernel Minimum Regularized Covariance Determinant (KMRCD) estimator addresses both issues. It is not restricted to elliptical data because it implicitly computes the MRCD estimates in a kernel induced feature space. A fast algorithm is constructed that starts from kernel-based initial estimates and exploits the kernel trick to speed up the subsequent computations. Based on the KMRCD estimates, a rule is proposed to flag outliers. The KMRCD algorithm performs well in simulations, and is illustrated on real-life data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge