Hannes De Meulemeester
Duality in Multi-View Restricted Kernel Machines
May 26, 2023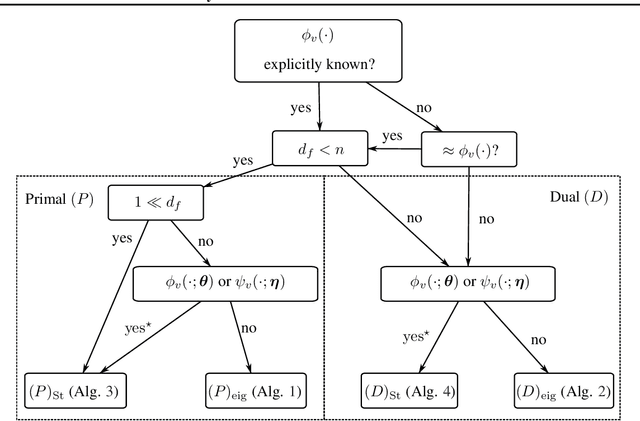
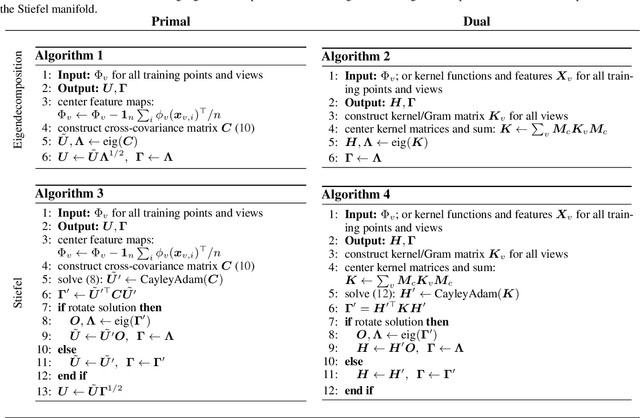
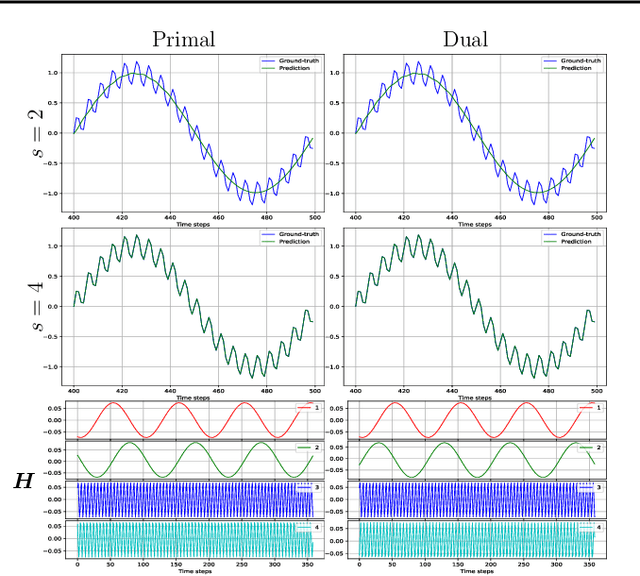
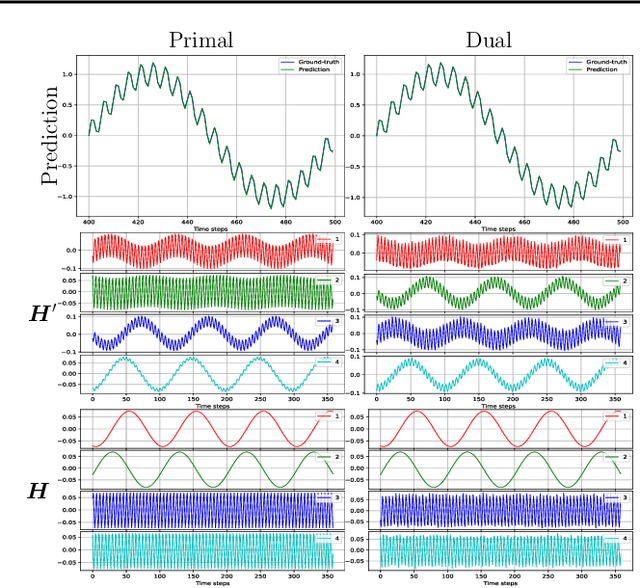
Abstract:We propose a unifying setting that combines existing restricted kernel machine methods into a single primal-dual multi-view framework for kernel principal component analysis in both supervised and unsupervised settings. We derive the primal and dual representations of the framework and relate different training and inference algorithms from a theoretical perspective. We show how to achieve full equivalence in primal and dual formulations by rescaling primal variables. Finally, we experimentally validate the equivalence and provide insight into the relationships between different methods on a number of time series data sets by recursively forecasting unseen test data and visualizing the learned features.
Multi-view Kernel PCA for Time series Forecasting
Jan 24, 2023Abstract:In this paper, we propose a kernel principal component analysis model for multi-variate time series forecasting, where the training and prediction schemes are derived from the multi-view formulation of Restricted Kernel Machines. The training problem is simply an eigenvalue decomposition of the summation of two kernel matrices corresponding to the views of the input and output data. When a linear kernel is used for the output view, it is shown that the forecasting equation takes the form of kernel ridge regression. When that kernel is non-linear, a pre-image problem has to be solved to forecast a point in the input space. We evaluate the model on several standard time series datasets, perform ablation studies, benchmark with closely related models and discuss its results.
Leverage Score Sampling for Complete Mode Coverage in Generative Adversarial Networks
Apr 27, 2021

Abstract:Commonly, machine learning models minimize an empirical expectation. As a result, the trained models typically perform well for the majority of the data but the performance may deteriorate on less dense regions of the dataset. This issue also arises in generative modeling. A generative model may overlook underrepresented modes that are less frequent in the empirical data distribution. This problem is known as complete mode coverage. We propose a sampling procedure based on ridge leverage scores which significantly improves mode coverage when compared to standard methods and can easily be combined with any GAN. Ridge Leverage Scores (RLSs) are computed by using an explicit feature map, associated with the next-to-last layer of a GAN discriminator or of a pre-trained network, or by using an implicit feature map corresponding to a Gaussian kernel. Multiple evaluations against recent approaches of complete mode coverage show a clear improvement when using the proposed sampling strategy.
The Bures Metric for Taming Mode Collapse in Generative Adversarial Networks
Jun 16, 2020
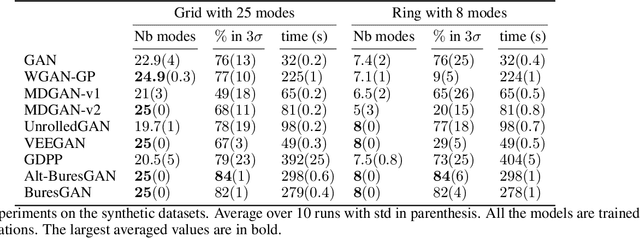

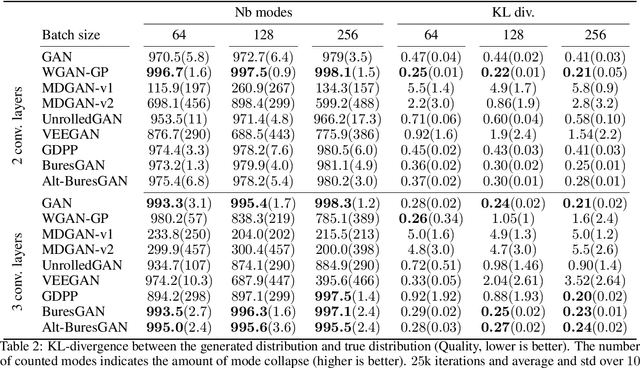
Abstract:Generative Adversarial Networks (GANs) are performant generative methods yielding high-quality samples. However, under certain circumstances, the training of GANs can lead to mode collapse or mode dropping, i.e. the generative models not being able to sample from the entire probability distribution. To address this problem, we use the last layer of the discriminator as a feature map to study the distribution of the real and the fake data. During training, we propose to match the real batch diversity to the fake batch diversity by using the Bures distance between covariance matrices in feature space. The computation of the Bures distance can be conveniently done in either feature space or kernel space in terms of the covariance and kernel matrix respectively. We observe that diversity matching reduces mode collapse substantially and has a positive effect on the sample quality. On the practical side, a very simple training procedure, that does not require additional hyperparameter tuning, is proposed and assessed on several datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge