On sampling determinantal and Pfaffian point processes on a quantum computer

DPPs were introduced by Macchi as a model in quantum optics the 1970s. Since then, they have been widely used as models and subsampling tools in statistics and computer science. Most applications require sampling from a DPP, and given their quantum origin, it is natural to wonder whether sampling a DPP on a quantum computer is easier than on a classical one. We focus here on DPPs over a finite state space, which are distributions over the subsets of $\{1,\dots,N\}$ parametrized by an $N\times N$ Hermitian kernel matrix. Vanilla sampling consists in two steps, of respective costs $\mathcal{O}(N^3)$ and $\mathcal{O}(Nr^2)$ operations on a classical computer, where $r$ is the rank of the kernel matrix. A large first part of the current paper consists in explaining why the state-of-the-art in quantum simulation of fermionic systems already yields quantum DPP sampling algorithms. We then modify existing quantum circuits, and discuss their insertion in a full DPP sampling pipeline that starts from practical kernel specifications. The bottom line is that, with $P$ (classical) parallel processors, we can divide the preprocessing cost by $P$ and build a quantum circuit with $\mathcal{O}(Nr)$ gates that sample a given DPP, with depth varying from $\mathcal{O}(N)$ to $\mathcal{O}(r\log N)$ depending on qubit-communication constraints on the target machine. We also connect existing work on the simulation of superconductors to Pfaffian point processes, which generalize DPPs and would be a natural addition to the machine learner's toolbox. Finally, the circuits are empirically validated on a classical simulator and on 5-qubit machines.

Sparsification of the regularized magnetic Laplacian with multi-type spanning forests

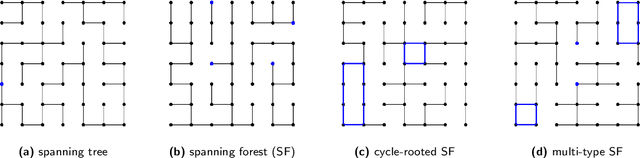
In this paper, we consider a ${\rm U}(1)$-connection graph, that is, a graph where each oriented edge is endowed with a unit modulus complex number which is simply conjugated under orientation flip. A natural replacement for the combinatorial Laplacian is then the so-called magnetic Laplacian, an Hermitian matrix that includes information about the graph's connection. Connection graphs and magnetic Laplacians appear, e.g., in the problem of angular synchronization. In the context of large and dense graphs, we study here sparsifiers of the magnetic Laplacian, i.e., spectral approximations based on subgraphs with few edges. Our approach relies on sampling multi-type spanning forests (MTSFs) using a custom determinantal point process, a distribution over edges that favours diversity. In a word, an MTSF is a spanning subgraph whose connected components are either trees or cycle-rooted trees. The latter partially capture the angular inconsistencies of the connection graph, and thus provide a way to compress information contained in the connection. Interestingly, when this connection graph has weakly inconsistent cycles, samples of this distribution can be obtained by using a random walk with cycle popping. We provide statistical guarantees for a choice of natural estimators of the connection Laplacian, and investigate the practical application of our sparsifiers in two applications.

Recovering Hölder smooth functions from noisy modulo samples

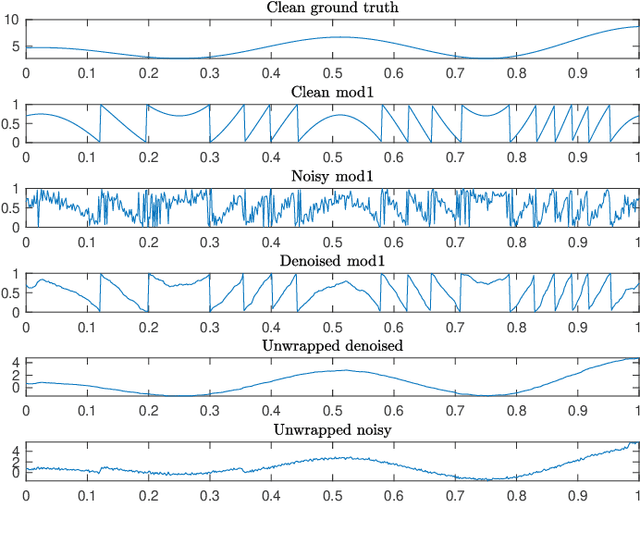
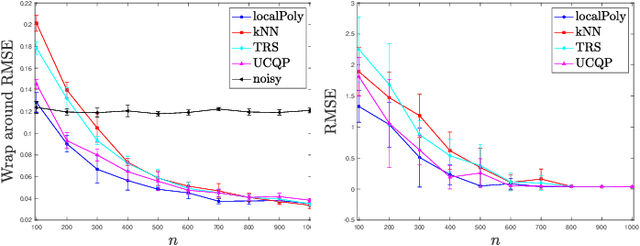
In signal processing, several applications involve the recovery of a function given noisy modulo samples. The setting considered in this paper is that the samples corrupted by an additive Gaussian noise are wrapped due to the modulo operation. Typical examples of this problem arise in phase unwrapping problems or in the context of self-reset analog to digital converters. We consider a fixed design setting where the modulo samples are given on a regular grid. Then, a three stage recovery strategy is proposed to recover the ground truth signal up to a global integer shift. The first stage denoises the modulo samples by using local polynomial estimators. In the second stage, an unwrapping algorithm is applied to the denoised modulo samples on the grid. Finally, a spline based quasi-interpolant operator is used to yield an estimate of the ground truth function up to a global integer shift. For a function in H\"older class, uniform error rates are given for recovery performance with high probability. This extends recent results obtained by Fanuel and Tyagi for Lipschitz smooth functions wherein $k$NN regression was used in the denoising step.

Nonparametric estimation of continuous DPPs with kernel methods

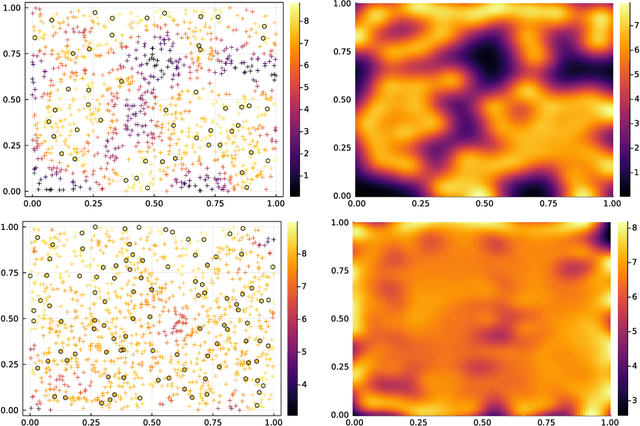
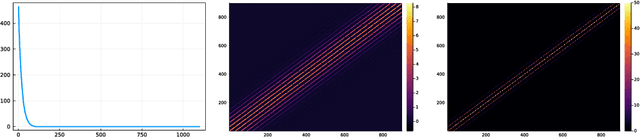
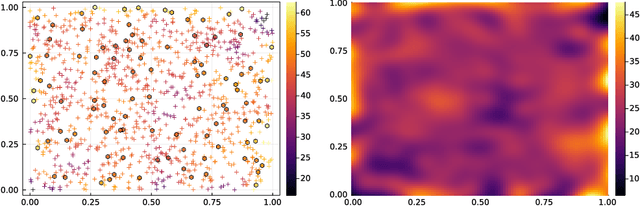
Determinantal Point Process (DPPs) are statistical models for repulsive point patterns. Both sampling and inference are tractable for DPPs, a rare feature among models with negative dependence that explains their popularity in machine learning and spatial statistics. Parametric and nonparametric inference methods have been proposed in the finite case, i.e. when the point patterns live in a finite ground set. In the continuous case, only parametric methods have been investigated, while nonparametric maximum likelihood for DPPs -- an optimization problem over trace-class operators -- has remained an open question. In this paper, we show that a restricted version of this maximum likelihood (MLE) problem falls within the scope of a recent representer theorem for nonnegative functions in an RKHS. This leads to a finite-dimensional problem, with strong statistical ties to the original MLE. Moreover, we propose, analyze, and demonstrate a fixed point algorithm to solve this finite-dimensional problem. Finally, we also provide a controlled estimate of the correlation kernel of the DPP, thus providing more interpretability.

Towards Deterministic Diverse Subset Sampling

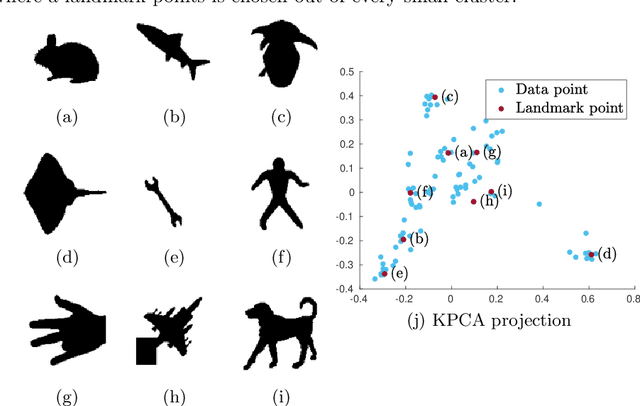
Determinantal point processes (DPPs) are well known models for diverse subset selection problems, including recommendation tasks, document summarization and image search. In this paper, we discuss a greedy deterministic adaptation of k-DPP. Deterministic algorithms are interesting for many applications, as they provide interpretability to the user by having no failure probability and always returning the same results. First, the ability of the method to yield low-rank approximations of kernel matrices is evaluated by comparing the accuracy of the Nystr\"om approximation on multiple datasets. Afterwards, we demonstrate the usefulness of the model on an image search task.

Leverage Score Sampling for Complete Mode Coverage in Generative Adversarial Networks

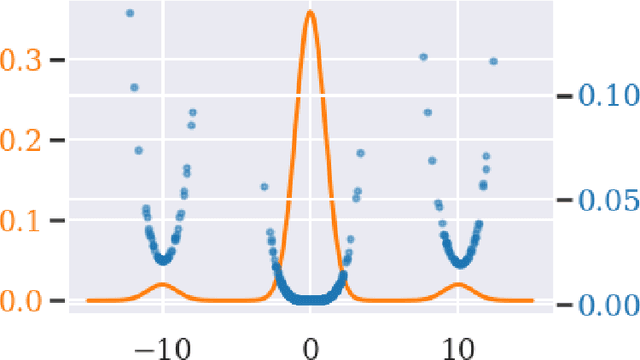
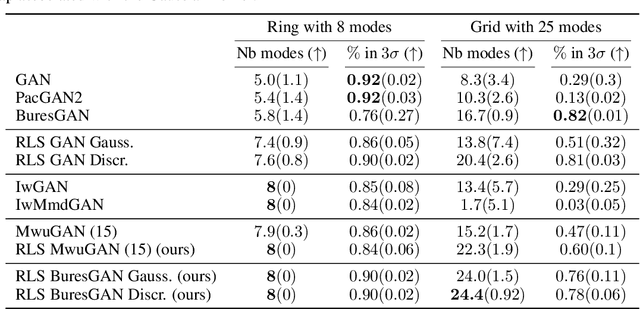
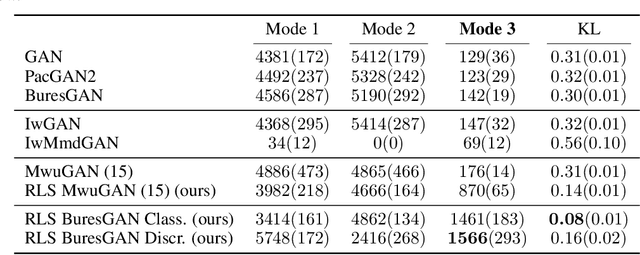
Commonly, machine learning models minimize an empirical expectation. As a result, the trained models typically perform well for the majority of the data but the performance may deteriorate on less dense regions of the dataset. This issue also arises in generative modeling. A generative model may overlook underrepresented modes that are less frequent in the empirical data distribution. This problem is known as complete mode coverage. We propose a sampling procedure based on ridge leverage scores which significantly improves mode coverage when compared to standard methods and can easily be combined with any GAN. Ridge Leverage Scores (RLSs) are computed by using an explicit feature map, associated with the next-to-last layer of a GAN discriminator or of a pre-trained network, or by using an implicit feature map corresponding to a Gaussian kernel. Multiple evaluations against recent approaches of complete mode coverage show a clear improvement when using the proposed sampling strategy.

Determinantal Point Processes Implicitly Regularize Semi-parametric Regression Problems

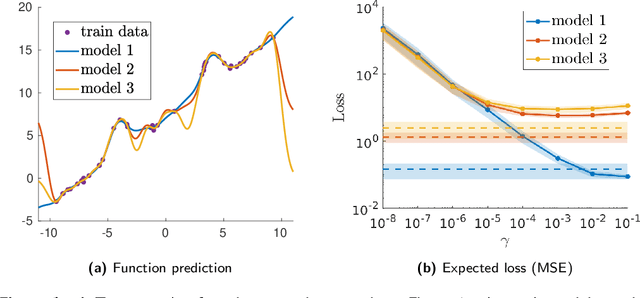
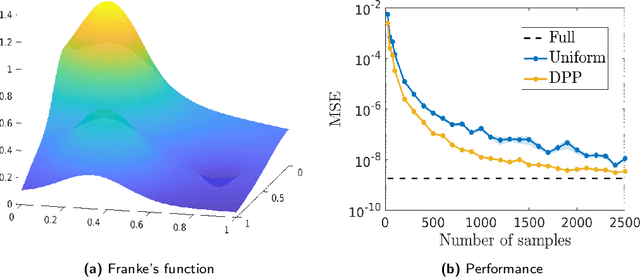
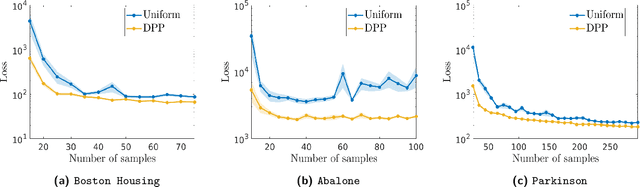
Semi-parametric regression models are used in several applications which require comprehensibility without sacrificing accuracy. Examples are spline interpolation in geophysics, or non-linear time series problems, where the system includes for instance a linear and non-linear component. We discuss here the use of a finite Determinantal Point Process (DPP) sampling for approximating semi-parametric models in two cases. On the one hand, in the case of large training data sets, DPP sampling is used to reduce the number of model parameters. On the other hand, DPPs can determine experimental designs in the case of the optimal interpolation models. Recently, Barthelm\'e, Tremblay, Usevich, and Amblard introduced a novel representation of finite DPP's. They formulated extended $L$-ensembles that can conveniently represent for instance partial-projection DPPs and suggest their use for optimal interpolation. With the help of this formalism, we derive a key identity illustrating the implicit regularization effect of determinantal sampling for semi-parametric regression and interpolation. Also, a novel projected Nystr\"om approximation is defined and used to derive a bound on the expected risk for the corresponding approximation of semi-parametric regression. This work naturally extends similar results obtained for kernel ridge regression.

Denoising modulo samples: k-NN regression and tightness of SDP relaxation

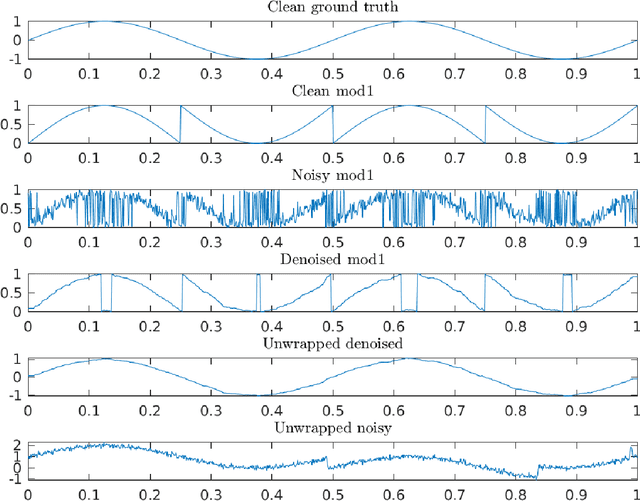
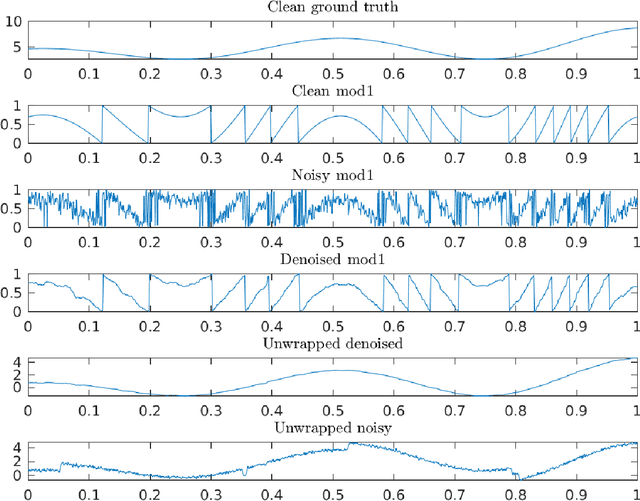
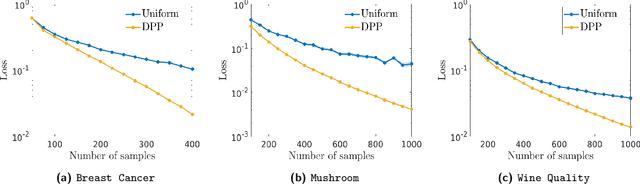
Many modern applications involve the acquisition of noisy modulo samples of a function $f$, with the goal being to recover estimates of the original samples of $f$. For a Lipschitz function $f:[0,1]^d \to \mathbb{R}$, suppose we are given the samples $y_i = (f(x_i) + \eta_i)\bmod 1; \quad i=1,\dots,n$ where $\eta_i$ denotes noise. Assuming $\eta_i$ are zero-mean i.i.d Gaussian's, and $x_i$'s form a uniform grid, we derive a two-stage algorithm that recovers estimates of the samples $f(x_i)$ with a uniform error rate $O((\frac{\log n}{n})^{\frac{1}{d+2}})$ holding with high probability. The first stage involves embedding the points on the unit complex circle, and obtaining denoised estimates of $f(x_i)\bmod 1$ via a $k$NN (nearest neighbor) estimator. The second stage involves a sequential unwrapping procedure which unwraps the denoised mod $1$ estimates from the first stage. Recently, Cucuringu and Tyagi proposed an alternative way of denoising modulo $1$ data which works with their representation on the unit complex circle. They formulated a smoothness regularized least squares problem on the product manifold of unit circles, where the smoothness is measured with respect to the Laplacian of a proximity graph $G$ involving the $x_i$'s. This is a nonconvex quadratically constrained quadratic program (QCQP) hence they proposed solving its semidefinite program (SDP) based relaxation. We derive sufficient conditions under which the SDP is a tight relaxation of the QCQP. Hence under these conditions, the global solution of QCQP can be obtained in polynomial time.

Ensemble Kernel Methods, Implicit Regularization and Determinantal Point Processes

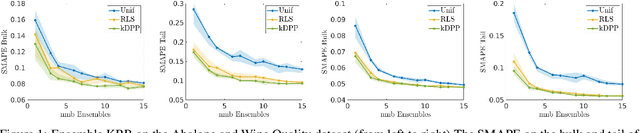
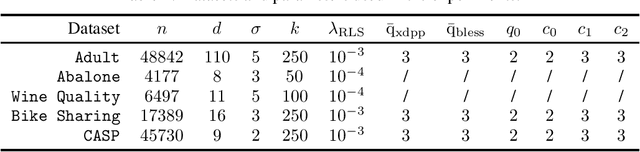
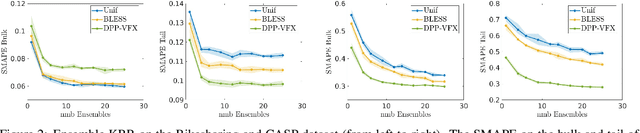
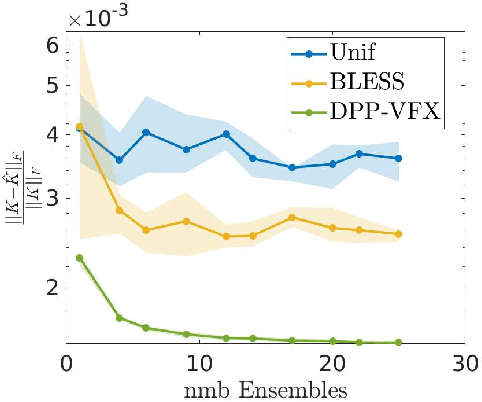
By using the framework of Determinantal Point Processes (DPPs), some theoretical results concerning the interplay between diversity and regularization can be obtained. In this paper we show that sampling subsets with kDPPs results in implicit regularization in the context of ridgeless Kernel Regression. Furthermore, we leverage the common setup of state-of-the-art DPP algorithms to sample multiple small subsets and use them in an ensemble of ridgeless regressions. Our first empirical results indicate that ensemble of ridgeless regressors can be interesting to use for datasets including redundant information.