Sparsification of the regularized magnetic Laplacian with multi-type spanning forests

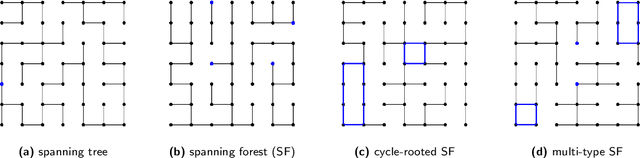
In this paper, we consider a ${\rm U}(1)$-connection graph, that is, a graph where each oriented edge is endowed with a unit modulus complex number which is simply conjugated under orientation flip. A natural replacement for the combinatorial Laplacian is then the so-called magnetic Laplacian, an Hermitian matrix that includes information about the graph's connection. Connection graphs and magnetic Laplacians appear, e.g., in the problem of angular synchronization. In the context of large and dense graphs, we study here sparsifiers of the magnetic Laplacian, i.e., spectral approximations based on subgraphs with few edges. Our approach relies on sampling multi-type spanning forests (MTSFs) using a custom determinantal point process, a distribution over edges that favours diversity. In a word, an MTSF is a spanning subgraph whose connected components are either trees or cycle-rooted trees. The latter partially capture the angular inconsistencies of the connection graph, and thus provide a way to compress information contained in the connection. Interestingly, when this connection graph has weakly inconsistent cycles, samples of this distribution can be obtained by using a random walk with cycle popping. We provide statistical guarantees for a choice of natural estimators of the connection Laplacian, and investigate the practical application of our sparsifiers in two applications.