Duality in Multi-View Restricted Kernel Machines
Paper and Code
May 26, 2023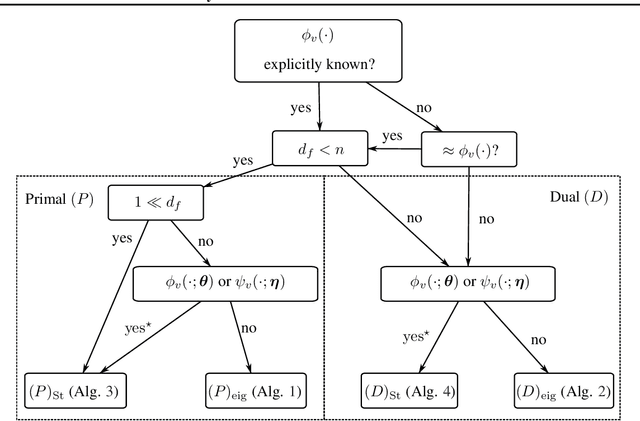
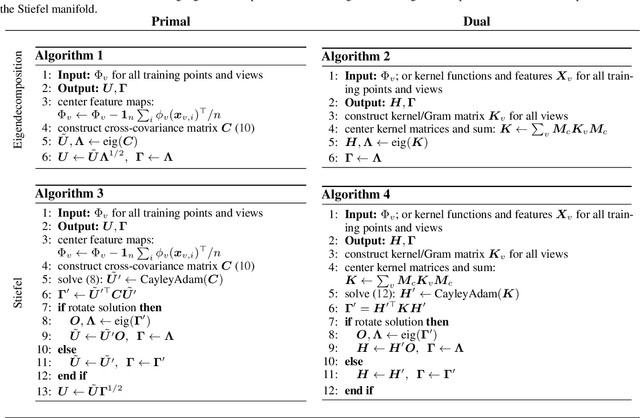
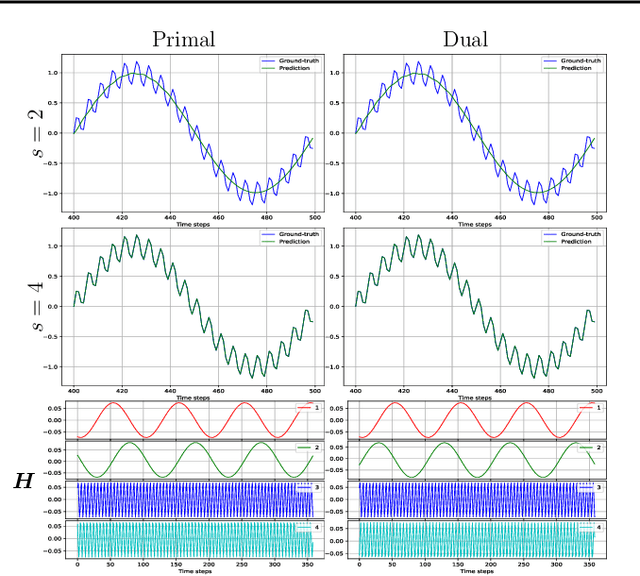
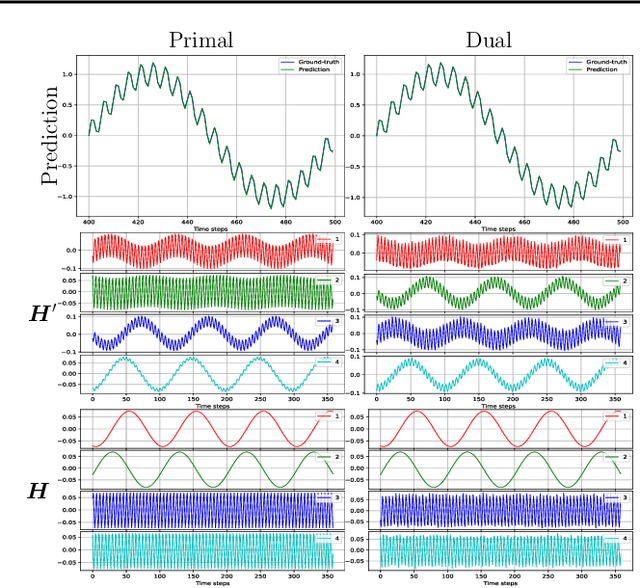
We propose a unifying setting that combines existing restricted kernel machine methods into a single primal-dual multi-view framework for kernel principal component analysis in both supervised and unsupervised settings. We derive the primal and dual representations of the framework and relate different training and inference algorithms from a theoretical perspective. We show how to achieve full equivalence in primal and dual formulations by rescaling primal variables. Finally, we experimentally validate the equivalence and provide insight into the relationships between different methods on a number of time series data sets by recursively forecasting unseen test data and visualizing the learned features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge