Diversity sampling is an implicit regularization for kernel methods
Paper and Code
Feb 20, 2020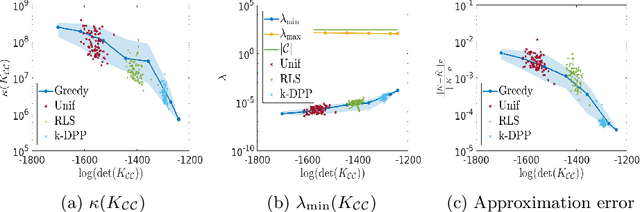
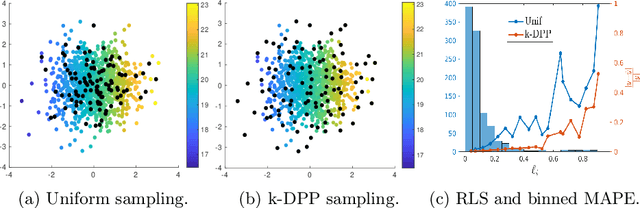

Kernel methods have achieved very good performance on large scale regression and classification problems, by using the Nystr\"om method and preconditioning techniques. The Nystr\"om approximation -- based on a subset of landmarks -- gives a low rank approximation of the kernel matrix, and is known to provide a form of implicit regularization. We further elaborate on the impact of sampling diverse landmarks for constructing the Nystr\"om approximation in supervised as well as unsupervised kernel methods. By using Determinantal Point Processes for sampling, we obtain additional theoretical results concerning the interplay between diversity and regularization. Empirically, we demonstrate the advantages of training kernel methods based on subsets made of diverse points. In particular, if the dataset has a dense bulk and a sparser tail, we show that Nystr\"om kernel regression with diverse landmarks increases the accuracy of the regression in sparser regions of the dataset, with respect to a uniform landmark sampling. A greedy heuristic is also proposed to select diverse samples of significant size within large datasets when exact DPP sampling is not practically feasible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge