A Multi-Phase Analysis of Blood Culture Stewardship: Machine Learning Prediction, Expert Recommendation Assessment, and LLM Automation

Blood cultures are often over ordered without clear justification, straining healthcare resources and contributing to inappropriate antibiotic use pressures worsened by the global shortage. In study of 135483 emergency department (ED) blood culture orders, we developed machine learning (ML) models to predict the risk of bacteremia using structured electronic health record (EHR) data and provider notes via a large language model (LLM). The structured models AUC improved from 0.76 to 0.79 with note embeddings and reached 0.81 with added diagnosis codes. Compared to an expert recommendation framework applied by human reviewers and an LLM-based pipeline, our ML approach offered higher specificity without compromising sensitivity. The recommendation framework achieved sensitivity 86%, specificity 57%, while the LLM maintained high sensitivity (96%) but over classified negatives, reducing specificity (16%). These findings demonstrate that ML models integrating structured and unstructured data can outperform consensus recommendations, enhancing diagnostic stewardship beyond existing standards of care.

Deconver: A Deconvolutional Network for Medical Image Segmentation

While convolutional neural networks (CNNs) and vision transformers (ViTs) have advanced medical image segmentation, they face inherent limitations such as local receptive fields in CNNs and high computational complexity in ViTs. This paper introduces Deconver, a novel network that integrates traditional deconvolution techniques from image restoration as a core learnable component within a U-shaped architecture. Deconver replaces computationally expensive attention mechanisms with efficient nonnegative deconvolution (NDC) operations, enabling the restoration of high-frequency details while suppressing artifacts. Key innovations include a backpropagation-friendly NDC layer based on a provably monotonic update rule and a parameter-efficient design. Evaluated across four datasets (ISLES'22, BraTS'23, GlaS, FIVES) covering both 2D and 3D segmentation tasks, Deconver achieves state-of-the-art performance in Dice scores and Hausdorff distance while reducing computational costs (FLOPs) by up to 90% compared to leading baselines. By bridging traditional image restoration with deep learning, this work offers a practical solution for high-precision segmentation in resource-constrained clinical workflows. The project is available at https://github.com/pashtari/deconver.

Antibiotic Resistance Microbiology Dataset (ARMD): A De-identified Resource for Studying Antimicrobial Resistance Using Electronic Health Records

The Antibiotic Resistance Microbiology Dataset (ARMD) is a de-identified resource derived from electronic health records (EHR) that facilitates research into antimicrobial resistance (AMR). ARMD encompasses data from adult patients, focusing on microbiological cultures, antibiotic susceptibilities, and associated clinical and demographic features. Key attributes include organism identification, susceptibility patterns for 55 antibiotics, implied susceptibility rules, and de-identified patient information. This dataset supports studies on antimicrobial stewardship, causal inference, and clinical decision-making. ARMD is designed to be reusable and interoperable, promoting collaboration and innovation in combating AMR. This paper describes the dataset's acquisition, structure, and utility while detailing its de-identification process.

Embedding-Driven Diversity Sampling to Improve Few-Shot Synthetic Data Generation

Accurate classification of clinical text often requires fine-tuning pre-trained language models, a process that is costly and time-consuming due to the need for high-quality data and expert annotators. Synthetic data generation offers an alternative, though pre-trained models may not capture the syntactic diversity of clinical notes. We propose an embedding-driven approach that uses diversity sampling from a small set of real clinical notes to guide large language models in few-shot prompting, generating synthetic text that better reflects clinical syntax. We evaluated this method using the CheXpert dataset on a classification task, comparing it to random few-shot and zero-shot approaches. Using cosine similarity and a Turing test, our approach produced synthetic notes that more closely align with real clinical text. Our pipeline reduced the data needed to reach the 0.85 AUC cutoff by 40% for AUROC and 30% for AUPRC, while augmenting models with synthetic data improved AUROC by 57% and AUPRC by 68%. Additionally, our synthetic data was 0.9 times as effective as real data, a 60% improvement in value.

Quantization-free Lossy Image Compression Using Integer Matrix Factorization

Lossy image compression is essential for efficient transmission and storage. Traditional compression methods mainly rely on discrete cosine transform (DCT) or singular value decomposition (SVD), both of which represent image data in continuous domains and therefore necessitate carefully designed quantizers. Notably, SVD-based methods are more sensitive to quantization errors than DCT-based methods like JPEG. To address this issue, we introduce a variant of integer matrix factorization (IMF) to develop a novel quantization-free lossy image compression method. IMF provides a low-rank representation of the image data as a product of two smaller factor matrices with bounded integer elements, thereby eliminating the need for quantization. We propose an efficient, provably convergent iterative algorithm for IMF using a block coordinate descent (BCD) scheme, with subproblems having closed-form solutions. Our experiments on the Kodak and CLIC 2024 datasets demonstrate that our IMF compression method consistently outperforms JPEG at low bit rates below 0.25 bits per pixel (bpp) and remains comparable at higher bit rates. We also assessed our method's capability to preserve visual semantics by evaluating an ImageNet pre-trained classifier on compressed images. Remarkably, our method improved top-1 accuracy by over 5 percentage points compared to JPEG at bit rates under 0.25 bpp. The project is available at https://github.com/pashtari/lrf .

Predicting Survival Outcomes in the Presence of Unlabeled Data

Many clinical studies require the follow-up of patients over time. This is challenging: apart from frequently observed drop-out, there are often also organizational and financial challenges, which can lead to reduced data collection and, in turn, can complicate subsequent analyses. In contrast, there is often plenty of baseline data available of patients with similar characteristics and background information, e.g., from patients that fall outside the study time window. In this article, we investigate whether we can benefit from the inclusion of such unlabeled data instances to predict accurate survival times. In other words, we introduce a third level of supervision in the context of survival analysis, apart from fully observed and censored instances, we also include unlabeled instances. We propose three approaches to deal with this novel setting and provide an empirical comparison over fifteen real-life clinical and gene expression survival datasets. Our results demonstrate that all approaches are able to increase the predictive performance over independent test data. We also show that integrating the partial supervision provided by censored data in a semi-supervised wrapper approach generally provides the best results, often achieving high improvements, compared to not using unlabeled data.

Supervised Fuzzy Partitioning

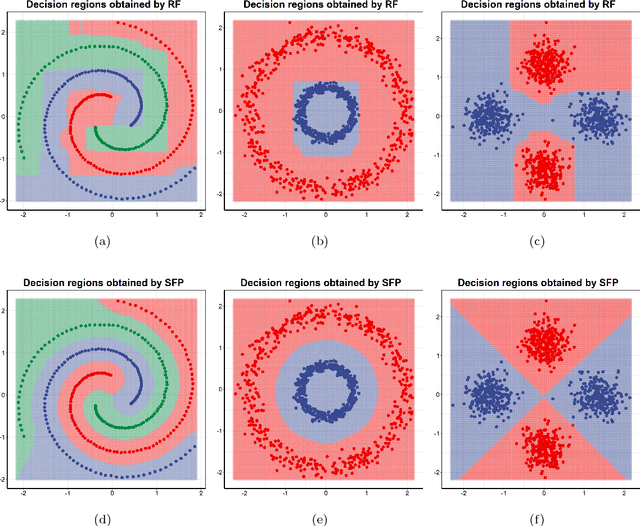
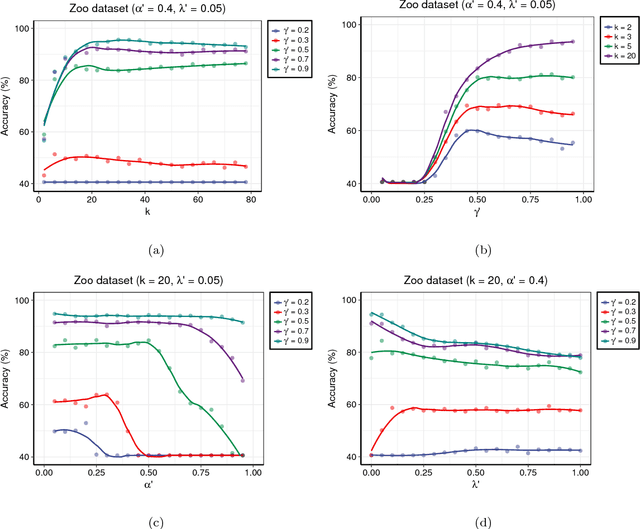
Centroid-based methods including k-means and fuzzy c-means are known as effective and easy-to-implement approaches to clustering purposes in many applications. However, these algorithms cannot be directly applied to supervised tasks. This paper thus presents a generative model extending the centroid-based clustering approach to be applicable to classification and regression tasks. Given an arbitrary loss function, the proposed approach, termed Supervised Fuzzy Partitioning (SFP), incorporates labels information into its objective function through a surrogate term penalizing the empirical risk. Entropy-based regularization is also employed to fuzzify the partition and to weight features, enabling the method to capture more complex patterns, identify significant features, and yield better performance facing high-dimensional data. An iterative algorithm based on block coordinate descent scheme is formulated to efficiently find a local optimum. Extensive classification experiments on synthetic, real-world, and high-dimensional datasets demonstrate that the predictive performance of SFP is competitive with state-of-the-art algorithms such as random forest and SVM. The SFP has a major advantage over such methods, in that it not only leads to a flexible, nonlinear model but also can exploit any convex loss function in the training phase without compromising computational efficiency.