Supervised Fuzzy Partitioning

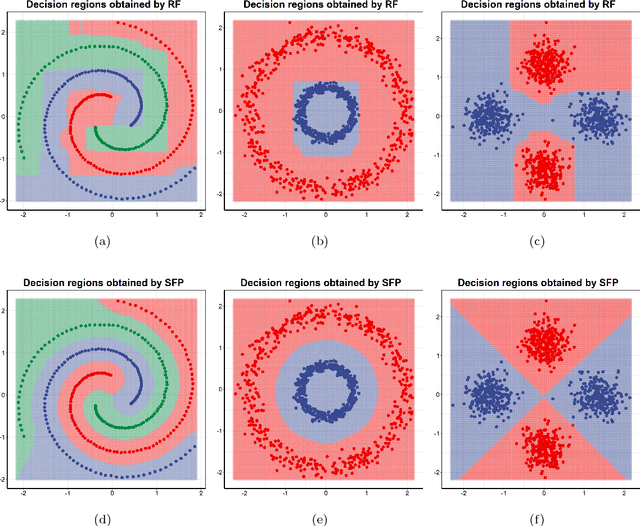
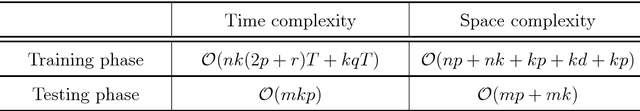
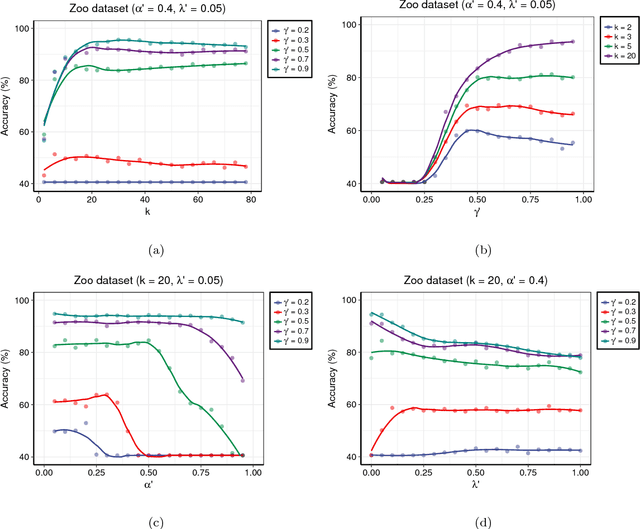
Centroid-based methods including k-means and fuzzy c-means are known as effective and easy-to-implement approaches to clustering purposes in many applications. However, these algorithms cannot be directly applied to supervised tasks. This paper thus presents a generative model extending the centroid-based clustering approach to be applicable to classification and regression tasks. Given an arbitrary loss function, the proposed approach, termed Supervised Fuzzy Partitioning (SFP), incorporates labels information into its objective function through a surrogate term penalizing the empirical risk. Entropy-based regularization is also employed to fuzzify the partition and to weight features, enabling the method to capture more complex patterns, identify significant features, and yield better performance facing high-dimensional data. An iterative algorithm based on block coordinate descent scheme is formulated to efficiently find a local optimum. Extensive classification experiments on synthetic, real-world, and high-dimensional datasets demonstrate that the predictive performance of SFP is competitive with state-of-the-art algorithms such as random forest and SVM. The SFP has a major advantage over such methods, in that it not only leads to a flexible, nonlinear model but also can exploit any convex loss function in the training phase without compromising computational efficiency.