Inertial Block Mirror Descent Method for Non-Convex Non-Smooth Optimization

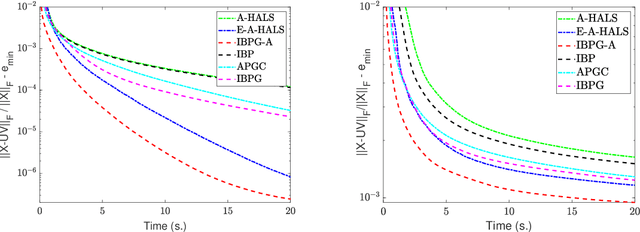
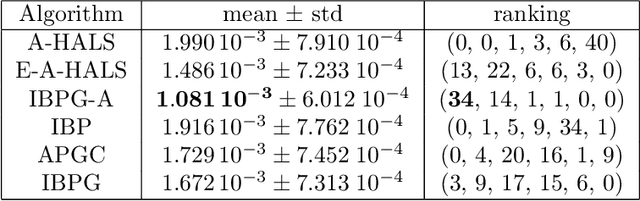
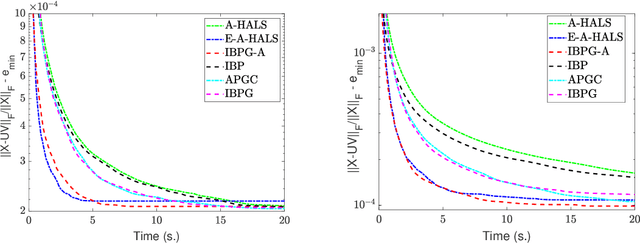
In this paper, we propose inertial versions of block coordinate descent methods for solving non-convex non-smooth composite optimization problems. We use the general framework of Bregman distance functions to compute the proximal maps. Our method not only allows using two different extrapolation points to evaluate gradients and adding the inertial force, but also takes advantage of randomly picking the block of variables to update. Moreover, our method does not require a restarting step, and as such, it is not a monotonically decreasing method. To prove the convergence of the whole generated sequence to a critical point, we modify the convergence proof recipe of Bolte, Sabach and Teboulle (Proximal alternating linearized minimization for non-convex and non-smooth problems, Math. Prog. 146(1):459--494, 2014), and combine it with auxiliary functions. We deploy the proposed methods to solve non-negative matrix factorization (NMF) problems and show that they compete favourably with the state-of-the-art NMF algorithms.