Efficient Algorithms for Regularized Nonnegative Scale-invariant Low-rank Approximation Models

Regularized nonnegative low-rank approximations such as sparse Nonnegative Matrix Factorization or sparse Nonnegative Tucker Decomposition are an important branch of dimensionality reduction models with enhanced interpretability. However, from a practical perspective, the choice of regularizers and regularization coefficients, as well as the design of efficient algorithms, is challenging because of the multifactor nature of these models and the lack of theory to back these choices. This paper aims at improving upon these issues. By studying a more general model called the Homogeneous Regularized Scale-Invariant, we prove that the scale-invariance inherent to low-rank approximation models causes an implicit regularization with both unexpected beneficial and detrimental effects. This observation allows to better understand the effect of regularization functions in low-rank approximation models, to guide the choice of the regularization hyperparameters, and to design balancing strategies to enhance the convergence speed of dedicated optimization algorithms. Some of these results were already known but restricted to specific instances of regularized low-rank approximations. We also derive a generic Majorization Minimization algorithm that handles many regularized nonnegative low-rank approximations, with convergence guarantees. We showcase our contributions on sparse Nonnegative Matrix Factorization, ridge-regularized Canonical Polyadic decomposition and sparse Nonnegative Tucker Decomposition.

Dictionary-based Low-Rank Approximations and the Mixed Sparse Coding problem

Constrained tensor and matrix factorization models allow to extract interpretable patterns from multiway data. Therefore identifiability properties and efficient algorithms for constrained low-rank approximations are nowadays important research topics. This work deals with columns of factor matrices of a low-rank approximation being sparse in a known and possibly overcomplete basis, a model coined as Dictionary-based Low-Rank Approximation (DLRA). While earlier contributions focused on finding factor columns inside a dictionary of candidate columns, i.e. one-sparse approximations, this work is the first to tackle DLRA with sparsity larger than one. I propose to focus on the sparse-coding subproblem coined Mixed Sparse-Coding (MSC) that emerges when solving DLRA with an alternating optimization strategy. Several algorithms based on sparse-coding heuristics (greedy methods, convex relaxations) are provided to solve MSC. The performance of these heuristics is evaluated on simulated data. Then, I show how to adapt an efficient MSC solver based on the LASSO to compute Dictionary-based Matrix Factorization and Canonical Polyadic Decomposition in the context of hyperspectral image processing and chemometrics. These experiments suggest that DLRA extends the modeling capabilities of low-rank approximations, helps reducing estimation variance and enhances the identifiability and interpretability of estimated factors.

An AO-ADMM approach to constraining PARAFAC2 on all modes

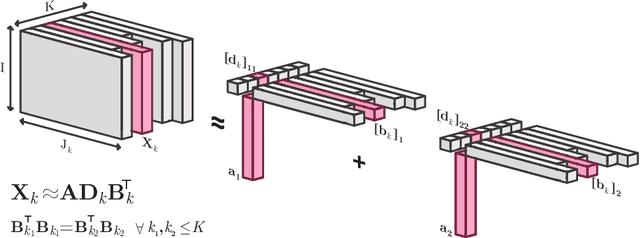
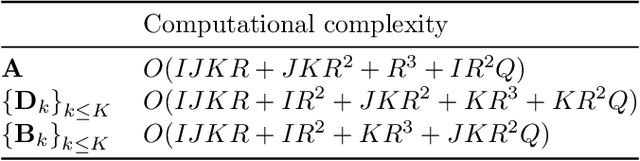
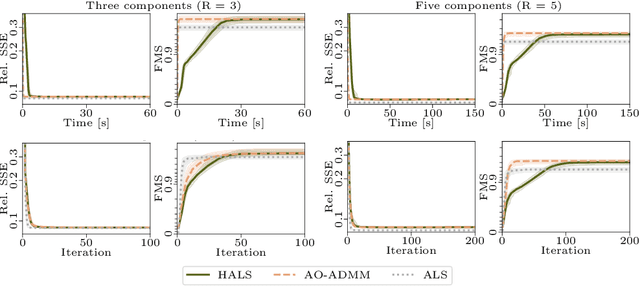
Analyzing multi-way measurements with variations across one mode of the dataset is a challenge in various fields including data mining, neuroscience and chemometrics. For example, measurements may evolve over time or have unaligned time profiles. The PARAFAC2 model has been successfully used to analyze such data by allowing the underlying factor matrices in one mode (i.e., the evolving mode) to change across slices. The traditional approach to fit a PARAFAC2 model is to use an alternating least squares-based algorithm, which handles the constant cross-product constraint of the PARAFAC2 model by implicitly estimating the evolving factor matrices. This approach makes imposing regularization on these factor matrices challenging. There is currently no algorithm to flexibly impose such regularization with general penalty functions and hard constraints. In order to address this challenge and to avoid the implicit estimation, in this paper, we propose an algorithm for fitting PARAFAC2 based on alternating optimization with the alternating direction method of multipliers (AO-ADMM). With numerical experiments on simulated data, we show that the proposed PARAFAC2 AO-ADMM approach allows for flexible constraints, recovers the underlying patterns accurately, and is computationally efficient compared to the state-of-the-art. We also apply our model to a real-world chromatography dataset, and show that constraining the evolving mode improves the interpretability of the extracted patterns.

PARAFAC2 AO-ADMM: Constraints in all modes

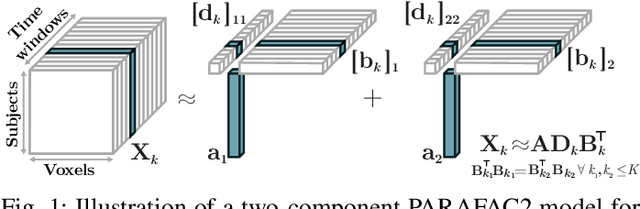
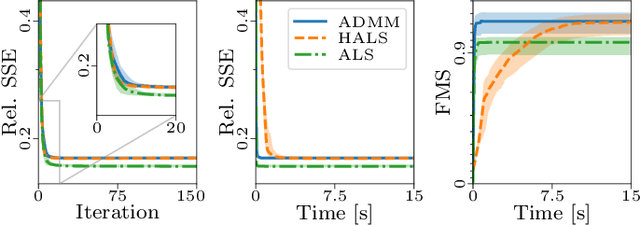
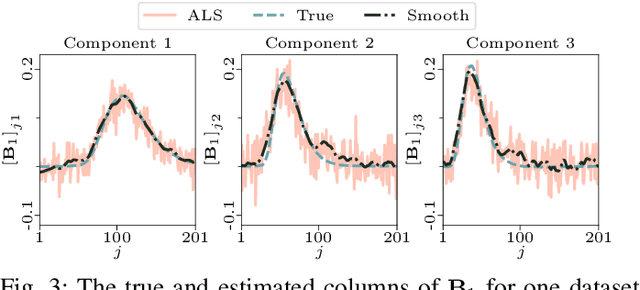
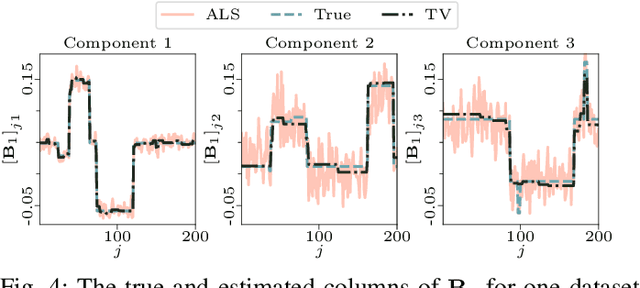
The PARAFAC2 model provides a flexible alternative to the popular CANDECOMP/PARAFAC (CP) model for tensor decompositions. Unlike CP, PARAFAC2 allows factor matrices in one mode (i.e., evolving mode) to change across tensor slices, which has proven useful for applications in different domains such as chemometrics, and neuroscience. However, the evolving mode of the PARAFAC2 model is traditionally modelled implicitly, which makes it challenging to regularise it. Currently, the only way to apply regularisation on that mode is with a flexible coupling approach, which finds the solution through regularised least-squares subproblems. In this work, we instead propose an alternating direction method of multipliers (ADMM)-based algorithm for fitting PARAFAC2 and widen the possible regularisation penalties to any proximable function. Our numerical experiments demonstrate that the proposed ADMM-based approach for PARAFAC2 can accurately recover the underlying components from simulated data while being both computationally efficient and flexible in terms of imposing constraints.

A Flexible Optimization Framework for Regularized Matrix-Tensor Factorizations with Linear Couplings

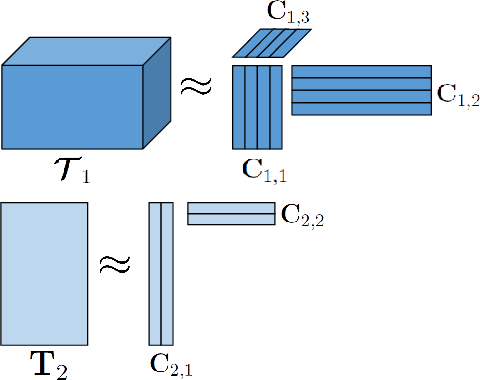
Coupled matrix and tensor factorizations (CMTF) are frequently used to jointly analyze data from multiple sources, also called data fusion. However, different characteristics of datasets stemming from multiple sources pose many challenges in data fusion and require to employ various regularizations, constraints, loss functions and different types of coupling structures between datasets. In this paper, we propose a flexible algorithmic framework for coupled matrix and tensor factorizations which utilizes Alternating Optimization (AO) and the Alternating Direction Method of Multipliers (ADMM). The framework facilitates the use of a variety of constraints, loss functions and couplings with linear transformations in a seamless way. Numerical experiments on simulated and real datasets demonstrate that the proposed approach is accurate, and computationally efficient with comparable or better performance than available CMTF methods for Frobenius norm loss, while being more flexible. Using Kullback-Leibler divergence on count data, we demonstrate that the algorithm yields accurate results also for other loss functions.

Sparse Separable Nonnegative Matrix Factorization

We propose a new variant of nonnegative matrix factorization (NMF), combining separability and sparsity assumptions. Separability requires that the columns of the first NMF factor are equal to columns of the input matrix, while sparsity requires that the columns of the second NMF factor are sparse. We call this variant sparse separable NMF (SSNMF), which we prove to be NP-complete, as opposed to separable NMF which can be solved in polynomial time. The main motivation to consider this new model is to handle underdetermined blind source separation problems, such as multispectral image unmixing. We introduce an algorithm to solve SSNMF, based on the successive nonnegative projection algorithm (SNPA, an effective algorithm for separable NMF), and an exact sparse nonnegative least squares solver. We prove that, in noiseless settings and under mild assumptions, our algorithm recovers the true underlying sources. This is illustrated by experiments on synthetic data sets and the unmixing of a multispectral image.

Accelerating Block Coordinate Descent for Nonnegative Tensor Factorization

This paper is concerned with improving the empirical convergence speed of block-coordinate descent algorithms for approximate nonnegative tensor factorization (NTF). We propose an extrapolation strategy in-between block updates, referred to as heuristic extrapolation with restarts (HER). HER significantly accelerates the empirical convergence speed of most existing block-coordinate algorithms for dense NTF, in particular for challenging computational scenarios, while requiring a negligible additional computational budget.

Nonnegative PARAFAC2: a flexible coupling approach

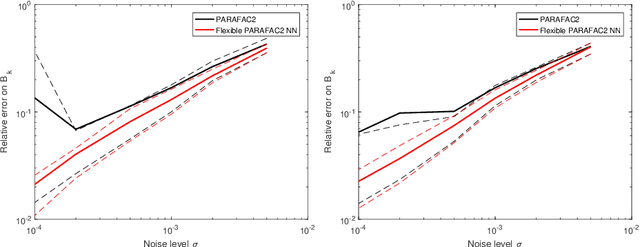
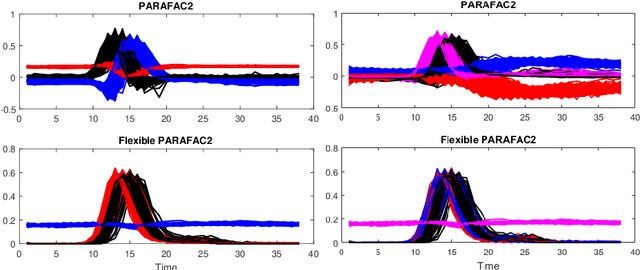
Modeling variability in tensor decomposition methods is one of the challenges of source separation. One possible solution to account for variations from one data set to another, jointly analysed, is to resort to the PARAFAC2 model. However, so far imposing constraints on the mode with variability has not been possible. In the following manuscript, a relaxation of the PARAFAC2 model is introduced, that allows for imposing nonnegativity constraints on the varying mode. An algorithm to compute the proposed flexible PARAFAC2 model is derived, and its performance is studied on both synthetic and chemometrics data.