Unfolding ADMM for Enhanced Subspace Clustering of Hyperspectral Images

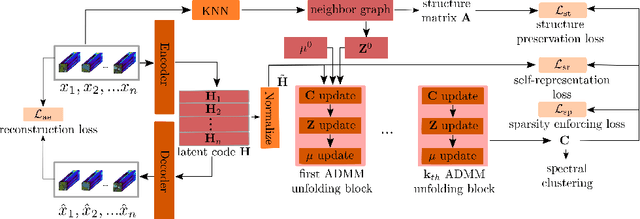
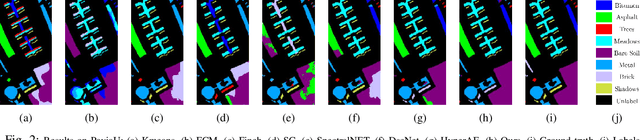
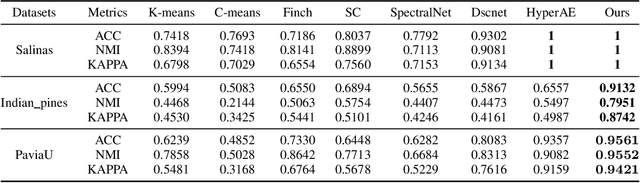
Deep subspace clustering methods are now prominent in clustering, typically using fully connected networks and a self-representation loss function. However, these methods often struggle with overfitting and lack interpretability. In this paper, we explore an alternative clustering approach based on deep unfolding. By unfolding iterative optimization methods into neural networks, this approach offers enhanced interpretability and reliability compared to data-driven deep learning methods, and greater adaptability and generalization than model-based approaches. Hence, unfolding has become widely used in inverse imaging problems, such as image restoration, reconstruction, and super-resolution, but has not been sufficiently explored yet in the context of clustering. In this work, we introduce an innovative clustering architecture for hyperspectral images (HSI) by unfolding an iterative solver based on the Alternating Direction Method of Multipliers (ADMM) for sparse subspace clustering. To our knowledge, this is the first attempt to apply unfolding ADMM for computing the self-representation matrix in subspace clustering. Moreover, our approach captures well the structural characteristics of HSI data by employing the K nearest neighbors algorithm as part of a structure preservation module. Experimental evaluation of three established HSI datasets shows clearly the potential of the unfolding approach in HSI clustering and even demonstrates superior performance compared to state-of-the-art techniques.

OsmLocator: locating overlapping scatter marks with a non-training generative perspective

Automated mark localization in scatter images, greatly helpful for discovering knowledge and understanding enormous document images and reasoning in visual question answering AI systems, is a highly challenging problem because of the ubiquity of overlapping marks. Locating overlapping marks faces many difficulties such as no texture, less contextual information, hallow shape and tiny size. Here, we formulate it as a combinatorial optimization problem on clustering-based re-visualization from a non-training generative perspective, to locate scatter marks by finding the status of multi-variables when an objective function reaches a minimum. The objective function is constructed on difference between binarized scatter images and corresponding generated re-visualization based on their clustering. Fundamentally, re-visualization tries to generate a new scatter graph only taking a rasterized scatter image as an input, and clustering is employed to provide the information for such re-visualization. This method could stably locate severely-overlapping, variable-size and variable-shape marks in scatter images without dependence of any training dataset or reference. Meanwhile, we propose an adaptive variant of simulated annealing which can works on various connected regions. In addition, we especially built a dataset named SML2023 containing hundreds of scatter images with different markers and various levels of overlapping severity, and tested the proposed method and compared it to existing methods. The results show that it can accurately locate most marks in scatter images with different overlapping severity and marker types, with about 0.3 absolute increase on an assignment-cost-based metric in comparison with state-of-the-art methods. This work is of value to data mining on massive web pages and literatures, and shedding new light on image measurement such as bubble counting.

Smoothed Separable Nonnegative Matrix Factorization

Given a set of data points belonging to the convex hull of a set of vertices, a key problem in data analysis and machine learning is to estimate these vertices in the presence of noise. Many algorithms have been developed under the assumption that there is at least one nearby data point to each vertex; two of the most widely used ones are vertex component analysis (VCA) and the successive projection algorithm (SPA). This assumption is known as the pure-pixel assumption in blind hyperspectral unmixing, and as the separability assumption in nonnegative matrix factorization. More recently, Bhattacharyya and Kannan (ACM-SIAM Symposium on Discrete Algorithms, 2020) proposed an algorithm for learning a latent simplex (ALLS) that relies on the assumption that there is more than one nearby data point for each vertex. In that scenario, ALLS is probalistically more robust to noise than algorithms based on the separability assumption. In this paper, inspired by ALLS, we propose smoothed VCA (SVCA) and smoothed SPA (SSPA) that generalize VCA and SPA by assuming the presence of several nearby data points to each vertex. We illustrate the effectiveness of SVCA and SSPA over VCA, SPA and ALLS on synthetic data sets, and on the unmixing of hyperspectral images.

A Homotopy-based Algorithm for Sparse Multiple Right-hand Sides Nonnegative Least Squares

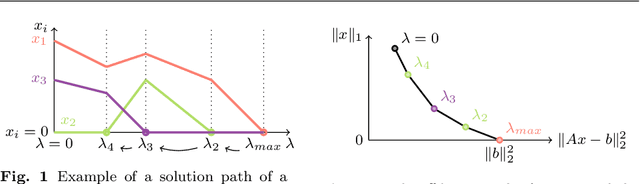
Nonnegative least squares (NNLS) problems arise in models that rely on additive linear combinations. In particular, they are at the core of nonnegative matrix factorization (NMF) algorithms. The nonnegativity constraint is known to naturally favor sparsity, that is, solutions with few non-zero entries. However, it is often useful to further enhance this sparsity, as it improves the interpretability of the results and helps reducing noise. While the $\ell_0$-"norm", equal to the number of non-zeros entries in a vector, is a natural sparsity measure, its combinatorial nature makes it difficult to use in practical optimization schemes. Most existing approaches thus rely either on its convex surrogate, the $\ell_1$-norm, or on heuristics such as greedy algorithms. In the case of multiple right-hand sides NNLS (MNNLS), which are used within NMF algorithms, sparsity is often enforced column- or row-wise, and the fact that the solution is a matrix is not exploited. In this paper, we first introduce a novel formulation for sparse MNNLS, with a matrix-wise $\ell_0$ sparsity constraint. Then, we present a two-step algorithm to tackle this problem. The first step uses a homotopy algorithm to produce the whole regularization path for all the $\ell_1$-penalized NNLS problems arising in MNNLS, that is, to produce a set of solutions representing different tradeoffs between reconstruction error and sparsity. The second step selects solutions among these paths in order to build a sparsity-constrained matrix that minimizes the reconstruction error. We illustrate the advantages of our proposed algorithm for the unmixing of facial and hyperspectral images.

Sparse Separable Nonnegative Matrix Factorization

We propose a new variant of nonnegative matrix factorization (NMF), combining separability and sparsity assumptions. Separability requires that the columns of the first NMF factor are equal to columns of the input matrix, while sparsity requires that the columns of the second NMF factor are sparse. We call this variant sparse separable NMF (SSNMF), which we prove to be NP-complete, as opposed to separable NMF which can be solved in polynomial time. The main motivation to consider this new model is to handle underdetermined blind source separation problems, such as multispectral image unmixing. We introduce an algorithm to solve SSNMF, based on the successive nonnegative projection algorithm (SNPA, an effective algorithm for separable NMF), and an exact sparse nonnegative least squares solver. We prove that, in noiseless settings and under mild assumptions, our algorithm recovers the true underlying sources. This is illustrated by experiments on synthetic data sets and the unmixing of a multispectral image.