Uncertainty quantification for fast reconstruction methods using augmented equivariant bootstrap: Application to radio interferometry

The advent of next-generation radio interferometers like the Square Kilometer Array promises to revolutionise our radio astronomy observational capabilities. The unprecedented volume of data these devices generate requires fast and accurate image reconstruction algorithms to solve the ill-posed radio interferometric imaging problem. Most state-of-the-art reconstruction methods lack trustworthy and scalable uncertainty quantification, which is critical for the rigorous scientific interpretation of radio observations. We propose an unsupervised technique based on a conformalized version of a radio-augmented equivariant bootstrapping method, which allows us to quantify uncertainties for fast reconstruction methods. Noticeably, we rely on reconstructions from ultra-fast unrolled algorithms. The proposed method brings more reliable uncertainty estimations to our problem than existing alternatives.

unrolling palm for sparse semi-blind source separation

Sparse Blind Source Separation (BSS) has become a well established tool for a wide range of applications - for instance, in astrophysics and remote sensing. Classical sparse BSS methods, such as the Proximal Alternating Linearized Minimization (PALM) algorithm, nevertheless often suffer from a difficult hyperparameter choice, which undermines their results. To bypass this pitfall, we propose in this work to build on the thriving field of algorithm unfolding/unrolling. Unrolling PALM enables to leverage the data-driven knowledge stemming from realistic simulations or ground-truth data by learning both PALM hyperparameters and variables. In contrast to most existing unrolled algorithms, which assume a fixed known dictionary during the training and testing phases, this article further emphasizes on the ability to deal with variable mixing matrices (a.k.a. dictionaries). The proposed Learned PALM (LPALM) algorithm thus enables to perform semi-blind source separation, which is key to increase the generalization of the learnt model in real-world applications. We illustrate the relevance of LPALM in astrophysical multispectral imaging: the algorithm not only needs up to $10^4-10^5$ times fewer iterations than PALM, but also improves the separation quality, while avoiding the cumbersome hyperparameter and initialization choice of PALM. We further show that LPALM outperforms other unrolled source separation methods in the semi-blind setting.

Smoothed Separable Nonnegative Matrix Factorization

Given a set of data points belonging to the convex hull of a set of vertices, a key problem in data analysis and machine learning is to estimate these vertices in the presence of noise. Many algorithms have been developed under the assumption that there is at least one nearby data point to each vertex; two of the most widely used ones are vertex component analysis (VCA) and the successive projection algorithm (SPA). This assumption is known as the pure-pixel assumption in blind hyperspectral unmixing, and as the separability assumption in nonnegative matrix factorization. More recently, Bhattacharyya and Kannan (ACM-SIAM Symposium on Discrete Algorithms, 2020) proposed an algorithm for learning a latent simplex (ALLS) that relies on the assumption that there is more than one nearby data point for each vertex. In that scenario, ALLS is probalistically more robust to noise than algorithms based on the separability assumption. In this paper, inspired by ALLS, we propose smoothed VCA (SVCA) and smoothed SPA (SSPA) that generalize VCA and SPA by assuming the presence of several nearby data points to each vertex. We illustrate the effectiveness of SVCA and SSPA over VCA, SPA and ALLS on synthetic data sets, and on the unmixing of hyperspectral images.

Provably robust blind source separation of linear-quadratic near-separable mixtures

In this work, we consider the problem of blind source separation (BSS) by departing from the usual linear model and focusing on the linear-quadratic (LQ) model. We propose two provably robust and computationally tractable algorithms to tackle this problem under separability assumptions which require the sources to appear as samples in the data set. The first algorithm generalizes the successive nonnegative projection algorithm (SNPA), designed for linear BSS, and is referred to as SNPALQ. By explicitly modeling the product terms inherent to the LQ model along the iterations of the SNPA scheme, the nonlinear contributions of the mixing are mitigated, thus improving the separation quality. SNPALQ is shown to be able to recover the ground truth factors that generated the data, even in the presence of noise. The second algorithm is a brute-force (BF) algorithm, which is used as a post-processing step for SNPALQ. It enables to discard the spurious (mixed) samples extracted by SNPALQ, thus broadening its applicability. The BF is in turn shown to be robust to noise under easier-to-check and milder conditions than SNPALQ. We show that SNPALQ with and without the BF postprocessing is relevant in realistic numerical experiments.

Heuristics for Efficient Sparse Blind Source Separation

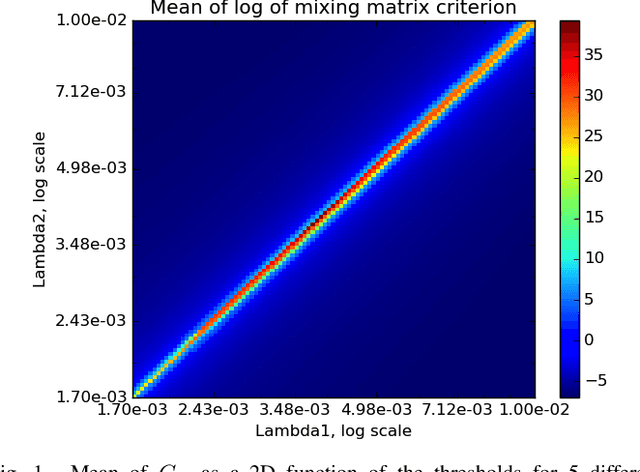
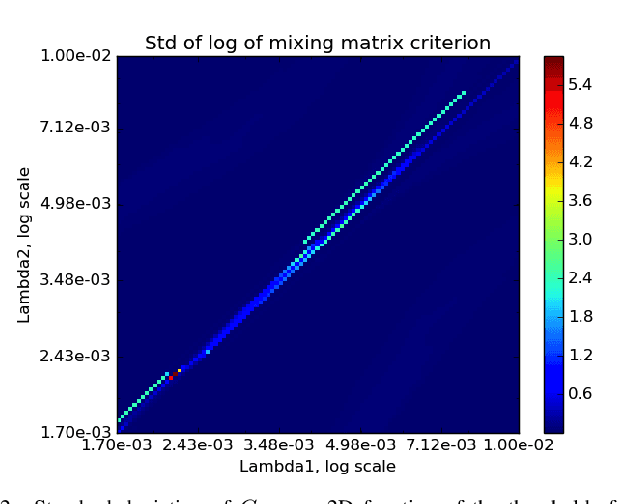
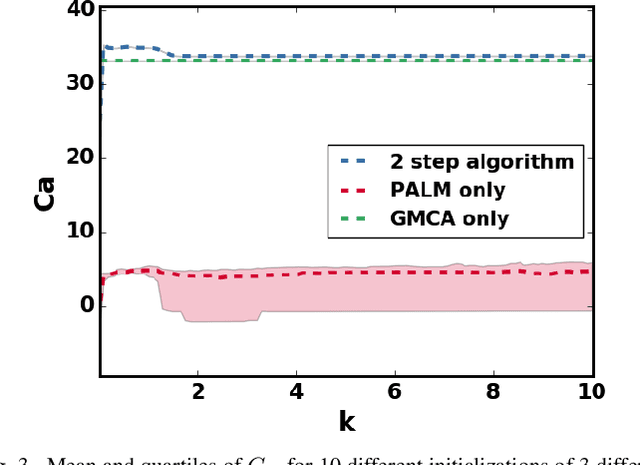
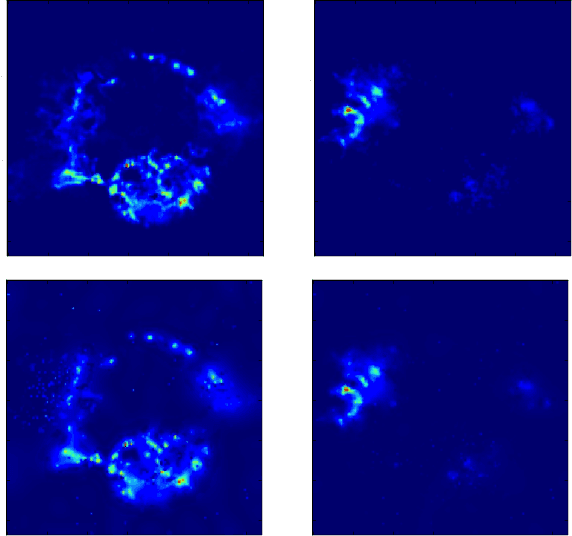
Sparse Blind Source Separation (sparse BSS) is a key method to analyze multichannel data in fields ranging from medical imaging to astrophysics. However, since it relies on seeking the solution of a non-convex penalized matrix factorization problem, its performances largely depend on the optimization strategy. In this context, Proximal Alternating Linearized Minimization (PALM) has become a standard algorithm which, despite its theoretical grounding, generally provides poor practical separation results. In this work, we propose a novel strategy that combines a heuristic approach with PALM. We show its relevance on realistic astrophysical data.