Uncertainty quantification for fast reconstruction methods using augmented equivariant bootstrap: Application to radio interferometry

The advent of next-generation radio interferometers like the Square Kilometer Array promises to revolutionise our radio astronomy observational capabilities. The unprecedented volume of data these devices generate requires fast and accurate image reconstruction algorithms to solve the ill-posed radio interferometric imaging problem. Most state-of-the-art reconstruction methods lack trustworthy and scalable uncertainty quantification, which is critical for the rigorous scientific interpretation of radio observations. We propose an unsupervised technique based on a conformalized version of a radio-augmented equivariant bootstrapping method, which allows us to quantify uncertainties for fast reconstruction methods. Noticeably, we rely on reconstructions from ultra-fast unrolled algorithms. The proposed method brings more reliable uncertainty estimations to our problem than existing alternatives.

MemSE: Fast MSE Prediction for Noisy Memristor-Based DNN Accelerators

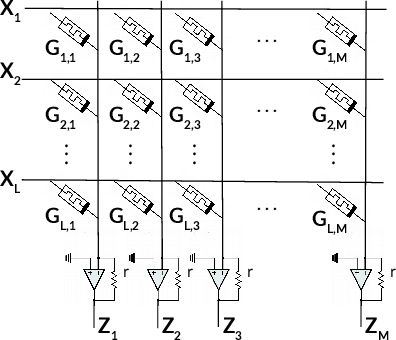
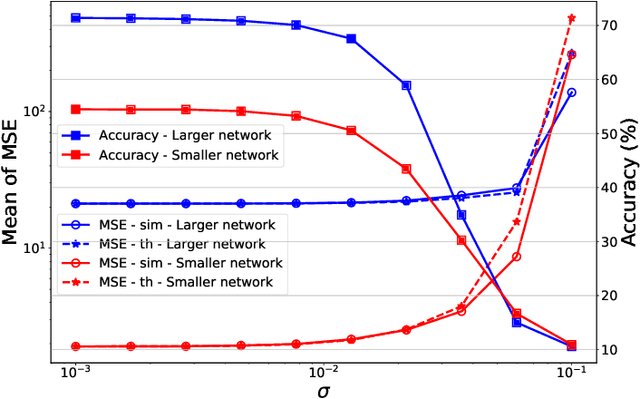
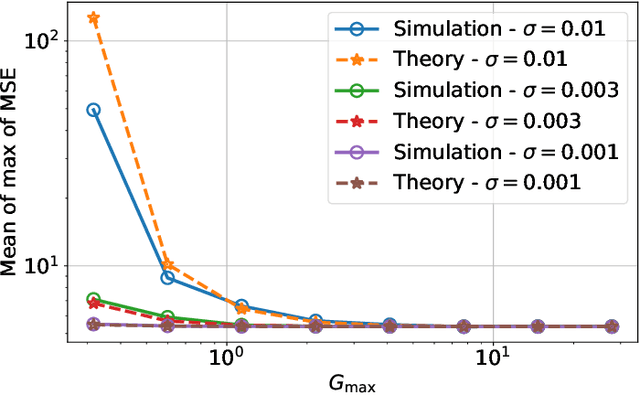
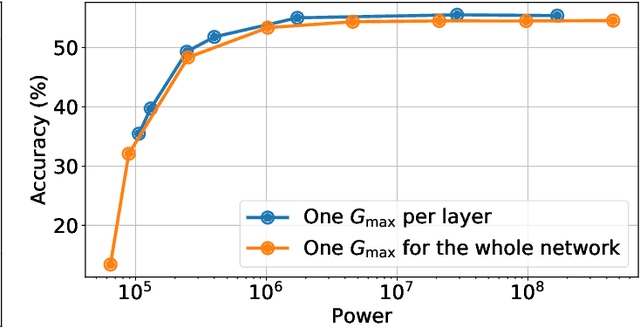
Memristors enable the computation of matrix-vector multiplications (MVM) in memory and, therefore, show great potential in highly increasing the energy efficiency of deep neural network (DNN) inference accelerators. However, computations in memristors suffer from hardware non-idealities and are subject to different sources of noise that may negatively impact system performance. In this work, we theoretically analyze the mean squared error of DNNs that use memristor crossbars to compute MVM. We take into account both the quantization noise, due to the necessity of reducing the DNN model size, and the programming noise, stemming from the variability during the programming of the memristance value. Simulations on pre-trained DNN models showcase the accuracy of the analytical prediction. Furthermore the proposed method is almost two order of magnitude faster than Monte-Carlo simulation, thus making it possible to optimize the implementation parameters to achieve minimal error for a given power constraint.

Optimizing the Energy Efficiency of Unreliable Memories for Quantized Kalman Filtering

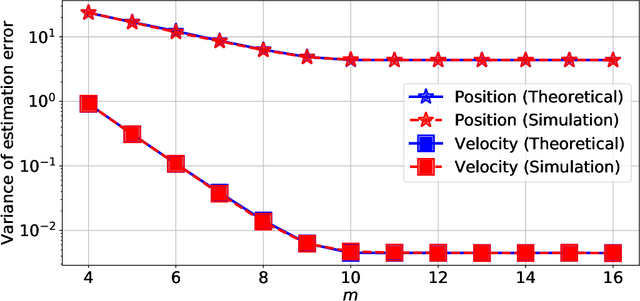
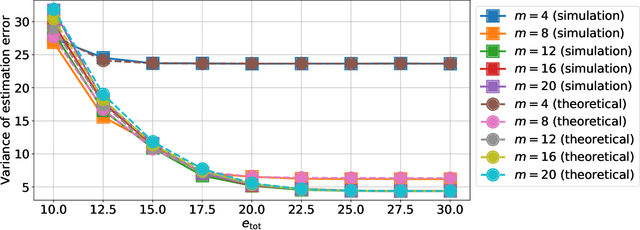
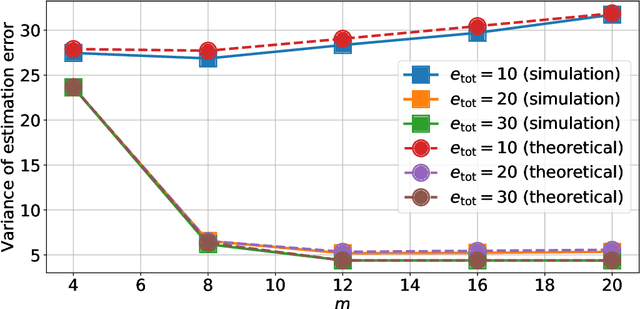
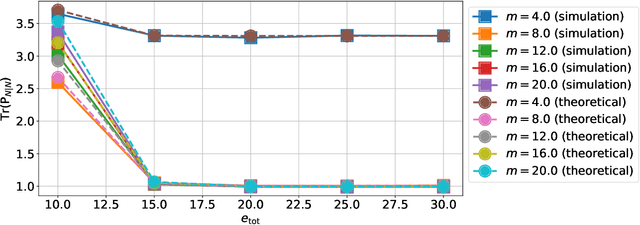
This paper presents a quantized Kalman filter implemented using unreliable memories. We consider that both the quantization and the unreliable memories introduce errors in the computations, and develop an error propagation model that takes into account these two sources of errors. In addition to providing updated Kalman filter equations, the proposed error model accurately predicts the covariance of the estimation error and gives a relation between the performance of the filter and its energy consumption, depending on the noise level in the memories. Then, since memories are responsible for a large part of the energy consumption of embedded systems, optimization methods are introduced so as to minimize the memory energy consumption under a desired estimation performance of the filter. The first method computes the optimal energy levels allocated to each memory bank individually, and the second one optimizes the energy allocation per groups of memory banks. Simulations show a close match between the theoretical analysis and experimental results. Furthermore, they demonstrate an important reduction in energy consumption of more than 50%.