Uncertainty quantification for fast reconstruction methods using augmented equivariant bootstrap: Application to radio interferometry

The advent of next-generation radio interferometers like the Square Kilometer Array promises to revolutionise our radio astronomy observational capabilities. The unprecedented volume of data these devices generate requires fast and accurate image reconstruction algorithms to solve the ill-posed radio interferometric imaging problem. Most state-of-the-art reconstruction methods lack trustworthy and scalable uncertainty quantification, which is critical for the rigorous scientific interpretation of radio observations. We propose an unsupervised technique based on a conformalized version of a radio-augmented equivariant bootstrapping method, which allows us to quantify uncertainties for fast reconstruction methods. Noticeably, we rely on reconstructions from ultra-fast unrolled algorithms. The proposed method brings more reliable uncertainty estimations to our problem than existing alternatives.

Semi-Blind Source Separation with Learned Constraints

Blind source separation (BSS) algorithms are unsupervised methods, which are the cornerstone of hyperspectral data analysis by allowing for physically meaningful data decompositions. BSS problems being ill-posed, the resolution requires efficient regularization schemes to better distinguish between the sources and yield interpretable solutions. For that purpose, we investigate a semi-supervised source separation approach in which we combine a projected alternating least-square algorithm with a learning-based regularization scheme. In this article, we focus on constraining the mixing matrix to belong to a learned manifold by making use of generative models. Altogether, we show that this allows for an innovative BSS algorithm, with improved accuracy, which provides physically interpretable solutions. The proposed method, coined sGMCA, is tested on realistic hyperspectral astrophysical data in challenging scenarios involving strong noise, highly correlated spectra and unbalanced sources. The results highlight the significant benefit of the learned prior to reduce the leakages between the sources, which allows an overall better disentanglement.

unrolling palm for sparse semi-blind source separation

Sparse Blind Source Separation (BSS) has become a well established tool for a wide range of applications - for instance, in astrophysics and remote sensing. Classical sparse BSS methods, such as the Proximal Alternating Linearized Minimization (PALM) algorithm, nevertheless often suffer from a difficult hyperparameter choice, which undermines their results. To bypass this pitfall, we propose in this work to build on the thriving field of algorithm unfolding/unrolling. Unrolling PALM enables to leverage the data-driven knowledge stemming from realistic simulations or ground-truth data by learning both PALM hyperparameters and variables. In contrast to most existing unrolled algorithms, which assume a fixed known dictionary during the training and testing phases, this article further emphasizes on the ability to deal with variable mixing matrices (a.k.a. dictionaries). The proposed Learned PALM (LPALM) algorithm thus enables to perform semi-blind source separation, which is key to increase the generalization of the learnt model in real-world applications. We illustrate the relevance of LPALM in astrophysical multispectral imaging: the algorithm not only needs up to $10^4-10^5$ times fewer iterations than PALM, but also improves the separation quality, while avoiding the cumbersome hyperparameter and initialization choice of PALM. We further show that LPALM outperforms other unrolled source separation methods in the semi-blind setting.

Joint deconvolution and unsupervised source separation for data on the sphere

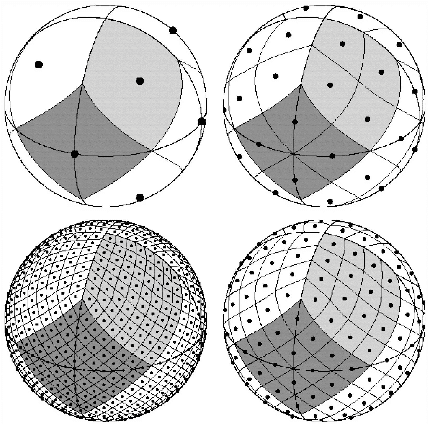
Tackling unsupervised source separation jointly with an additional inverse problem such as deconvolution is central for the analysis of multi-wavelength data. This becomes highly challenging when applied to large data sampled on the sphere such as those provided by wide-field observations in astrophysics, whose analysis requires the design of dedicated robust and yet effective algorithms. We therefore investigate a new joint deconvolution/sparse blind source separation method dedicated for data sampled on the sphere, coined SDecGMCA. It is based on a projected alternate least-squares minimization scheme, whose accuracy is proved to strongly rely on some regularization scheme in the present joint deconvolution/blind source separation setting. To this end, a regularization strategy is introduced that allows designing a new robust and effective algorithm, which is key to analyze large spherical data. Numerical experiments are carried out on toy examples and realistic astronomical data.

Two-pixel polarimetric camera by compressive sensing

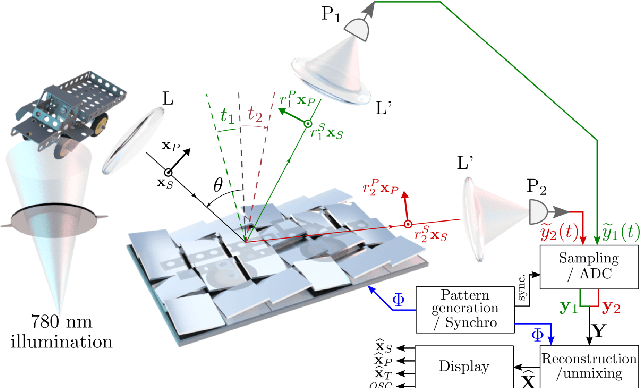
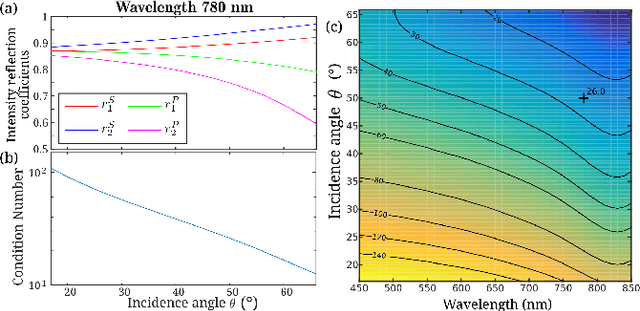
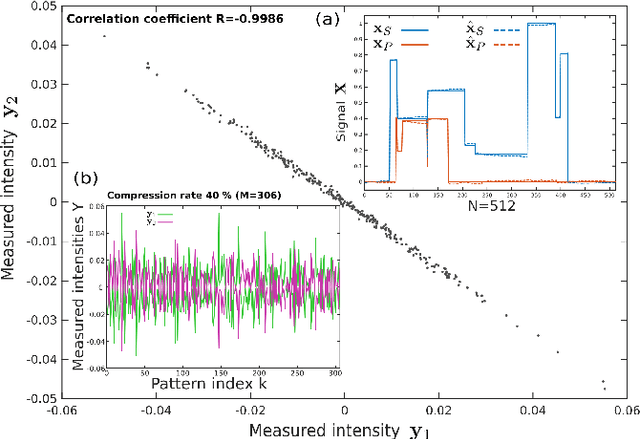
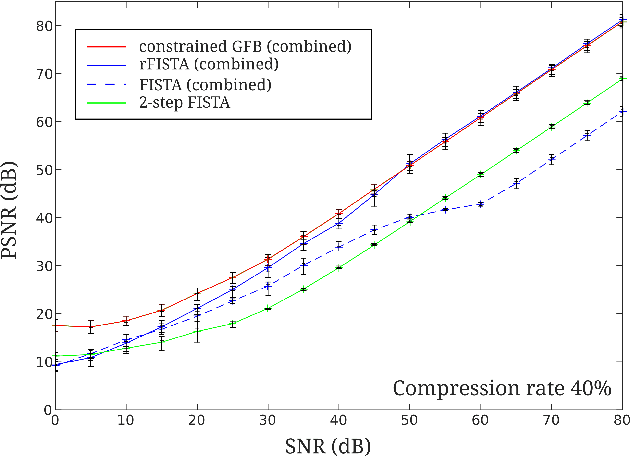
We propose an original concept of compressive sensing (CS) polarimetric imaging based on a digital micro-mirror (DMD) array and two single-pixel detectors. The polarimetric sensitivity of the proposed setup is due to an experimental imperfection of reflecting mirrors which is exploited here to form an original reconstruction problem, including a CS problem and a source separation task. We show that a two-step approach tackling each problem successively is outperformed by a dedicated combined reconstruction method, which is explicited in this article and preferably implemented through a reweighted FISTA algorithm. The combined reconstruction approach is then further improved by including physical constraints specific to the polarimetric imaging context considered, which are implemented in an original constrained GFB algorithm. Numerical simulations demonstrate the efficiency of the 2-pixel CS polarimetric imaging setup to retrieve polarimetric contrast data with significant compression rate and good reconstruction quality. The influence of experimental imperfections of the DMD are also analyzed through numerical simulations, and 2D polarimetric imaging reconstruction results are finally presented.

NMF with Sparse Regularizations in Transformed Domains

Non-negative blind source separation (non-negative BSS), which is also referred to as non-negative matrix factorization (NMF), is a very active field in domains as different as astrophysics, audio processing or biomedical signal processing. In this context, the efficient retrieval of the sources requires the use of signal priors such as sparsity. If NMF has now been well studied with sparse constraints in the direct domain, only very few algorithms can encompass non-negativity together with sparsity in a transformed domain since simultaneously dealing with two priors in two different domains is challenging. In this article, we show how a sparse NMF algorithm coined non-negative generalized morphological component analysis (nGMCA) can be extended to impose non-negativity in the direct domain along with sparsity in a transformed domain, with both analysis and synthesis formulations. To our knowledge, this work presents the first comparison of analysis and synthesis priors ---as well as their reweighted versions--- in the context of blind source separation. Comparisons with state-of-the-art NMF algorithms on realistic data show the efficiency as well as the robustness of the proposed algorithms.

Sparse and Non-Negative BSS for Noisy Data

Non-negative blind source separation (BSS) has raised interest in various fields of research, as testified by the wide literature on the topic of non-negative matrix factorization (NMF). In this context, it is fundamental that the sources to be estimated present some diversity in order to be efficiently retrieved. Sparsity is known to enhance such contrast between the sources while producing very robust approaches, especially to noise. In this paper we introduce a new algorithm in order to tackle the blind separation of non-negative sparse sources from noisy measurements. We first show that sparsity and non-negativity constraints have to be carefully applied on the sought-after solution. In fact, improperly constrained solutions are unlikely to be stable and are therefore sub-optimal. The proposed algorithm, named nGMCA (non-negative Generalized Morphological Component Analysis), makes use of proximal calculus techniques to provide properly constrained solutions. The performance of nGMCA compared to other state-of-the-art algorithms is demonstrated by numerical experiments encompassing a wide variety of settings, with negligible parameter tuning. In particular, nGMCA is shown to provide robustness to noise and performs well on synthetic mixtures of real NMR spectra.