Learning on JPEG-LDPC Compressed Images: Classifying with Syndromes

In goal-oriented communications, the objective of the receiver is often to apply a Deep-Learning model, rather than reconstructing the original data. In this context, direct learning over compressed data, without any prior decoding, holds promise for enhancing the time-efficient execution of inference models at the receiver. However, conventional entropic-coding methods like Huffman and Arithmetic break data structure, rendering them unsuitable for learning without decoding. In this paper, we propose an alternative approach in which entropic coding is realized with Low-Density Parity Check (LDPC) codes. We hypothesize that Deep Learning models can more effectively exploit the internal code structure of LDPC codes. At the receiver, we leverage a specific class of Recurrent Neural Networks (RNNs), specifically Gated Recurrent Unit (GRU), trained for image classification. Our numerical results indicate that classification based on LDPC-coded bit-planes surpasses Huffman and Arithmetic coding, while necessitating a significantly smaller learning model. This demonstrates the efficiency of classification directly from LDPC-coded data, eliminating the need for any form of decompression, even partial, prior to applying the learning model.

MemSE: Fast MSE Prediction for Noisy Memristor-Based DNN Accelerators

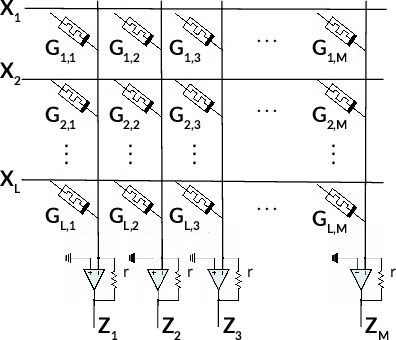
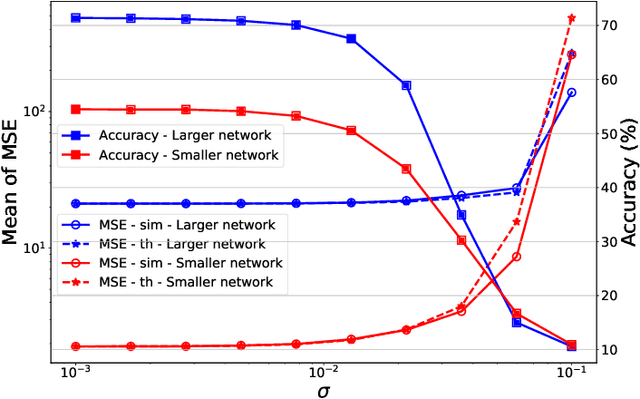
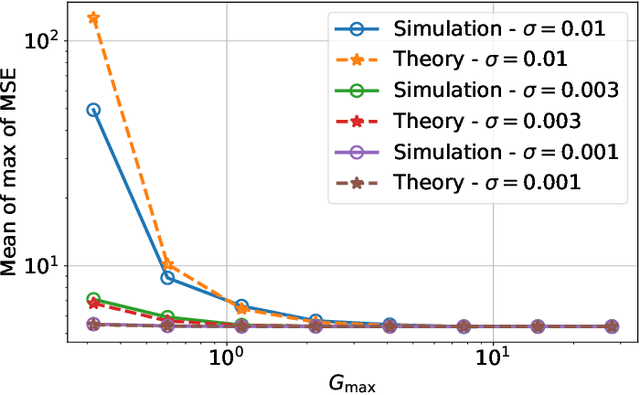
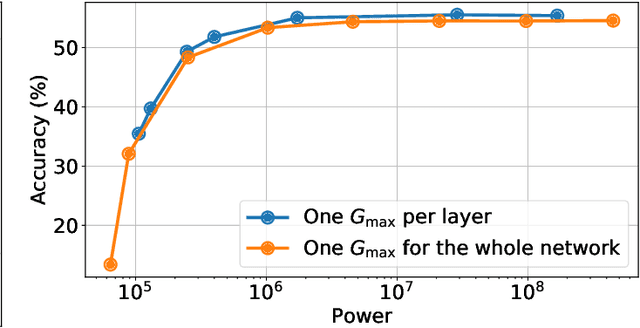
Memristors enable the computation of matrix-vector multiplications (MVM) in memory and, therefore, show great potential in highly increasing the energy efficiency of deep neural network (DNN) inference accelerators. However, computations in memristors suffer from hardware non-idealities and are subject to different sources of noise that may negatively impact system performance. In this work, we theoretically analyze the mean squared error of DNNs that use memristor crossbars to compute MVM. We take into account both the quantization noise, due to the necessity of reducing the DNN model size, and the programming noise, stemming from the variability during the programming of the memristance value. Simulations on pre-trained DNN models showcase the accuracy of the analytical prediction. Furthermore the proposed method is almost two order of magnitude faster than Monte-Carlo simulation, thus making it possible to optimize the implementation parameters to achieve minimal error for a given power constraint.

Optimizing the Energy Efficiency of Unreliable Memories for Quantized Kalman Filtering

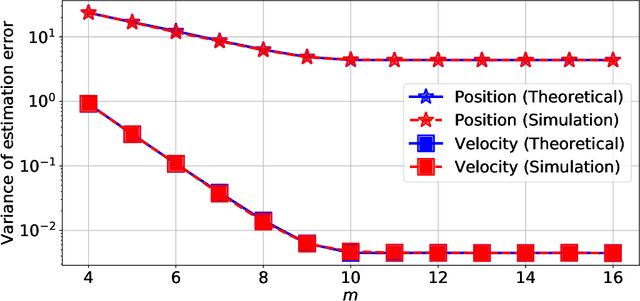
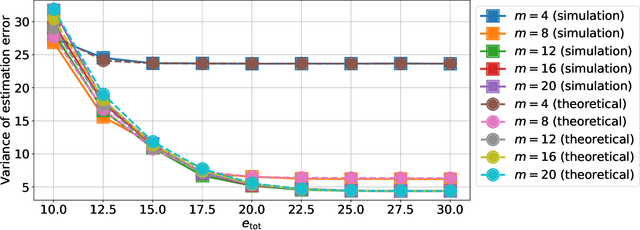
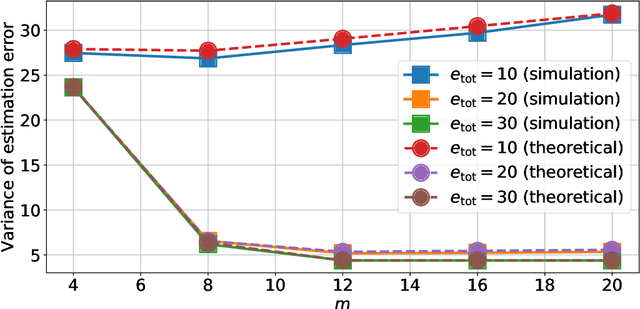
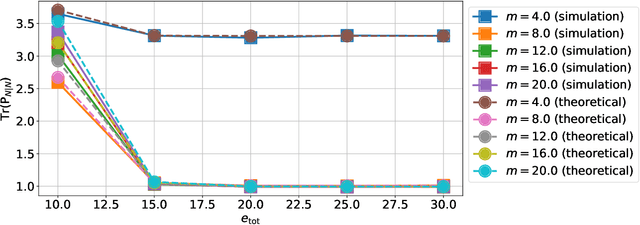
This paper presents a quantized Kalman filter implemented using unreliable memories. We consider that both the quantization and the unreliable memories introduce errors in the computations, and develop an error propagation model that takes into account these two sources of errors. In addition to providing updated Kalman filter equations, the proposed error model accurately predicts the covariance of the estimation error and gives a relation between the performance of the filter and its energy consumption, depending on the noise level in the memories. Then, since memories are responsible for a large part of the energy consumption of embedded systems, optimization methods are introduced so as to minimize the memory energy consumption under a desired estimation performance of the filter. The first method computes the optimal energy levels allocated to each memory bank individually, and the second one optimizes the energy allocation per groups of memory banks. Simulations show a close match between the theoretical analysis and experimental results. Furthermore, they demonstrate an important reduction in energy consumption of more than 50%.

Decentralized Clustering on Compressed Data without Prior Knowledge of the Number of Clusters

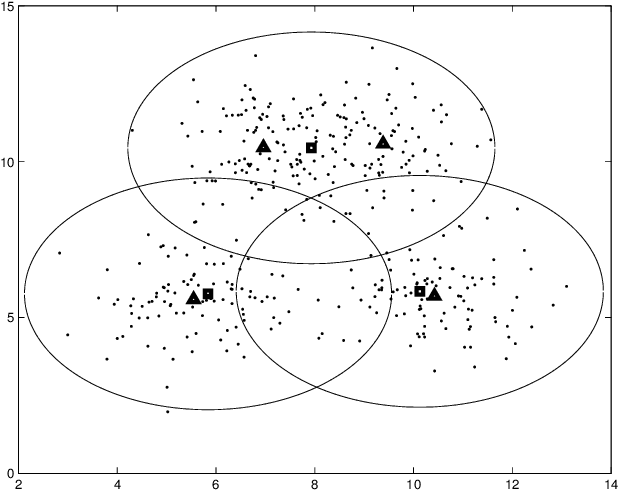
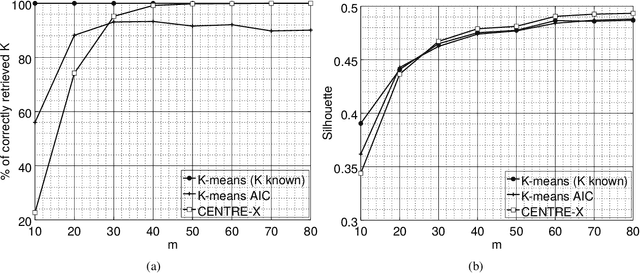
In sensor networks, it is not always practical to set up a fusion center. Therefore, there is need for fully decentralized clustering algorithms. Decentralized clustering algorithms should minimize the amount of data exchanged between sensors in order to reduce sensor energy consumption. In this respect, we propose one centralized and one decentralized clustering algorithm that work on compressed data without prior knowledge of the number of clusters. In the standard K-means clustering algorithm, the number of clusters is estimated by repeating the algorithm several times, which dramatically increases the amount of exchanged data, while our algorithm can estimate this number in one run. The proposed clustering algorithms derive from a theoretical framework establishing that, under asymptotic conditions, the cluster centroids are the only fixed-point of a cost function we introduce. This cost function depends on a weight function which we choose as the p-value of a Wald hypothesis test. This p-value measures the plausibility that a given measurement vector belongs to a given cluster. Experimental results show that our two algorithms are competitive in terms of clustering performance with respect to K-means and DB-Scan, while lowering by a factor at least $2$ the amount of data exchanged between sensors.