Parametric Rectified Power Sigmoid Units: Learning Nonlinear Neural Transfer Analytical Forms

The paper proposes representation functionals in a dual paradigm where learning jointly concerns both linear convolutional weights and parametric forms of nonlinear activation functions. The nonlinear forms proposed for performing the functional representation are associated with a new class of parametric neural transfer functions called rectified power sigmoid units. This class is constructed to integrate both advantages of sigmoid and rectified linear unit functions, in addition with rejecting the drawbacks of these functions. Moreover, the analytic form of this new neural class involves scale, shift and shape parameters so as to obtain a wide range of activation shapes, including the standard rectified linear unit as a limit case. Parameters of this neural transfer class are considered as learnable for the sake of discovering the complex shapes that can contribute in solving machine learning issues. Performance achieved by the joint learning of convolutional and rectified power sigmoid learnable parameters are shown outstanding in both shallow and deep learning frameworks. This class opens new prospects with respect to machine learning in the sense that learnable parameters are not only attached to linear transformations, but also to suitable nonlinear operators.

Convolutional neural networks on irregular domains based on approximate vertex-domain translations

We propose a generalization of convolutional neural networks (CNNs) to irregular domains, through the use of a translation operator on a graph structure. In regular settings such as images, convolutional layers are designed by translating a convolutional kernel over all pixels, thus enforcing translation equivariance. In the case of general graphs however, translation is not a well-defined operation, which makes shifting a convolutional kernel not straightforward. In this article, we introduce a methodology to allow the design of convolutional layers that are adapted to signals evolving on irregular topologies, even in the absence of a natural translation. Using the designed layers, we build a CNN that we train using the initial set of signals. Contrary to other approaches that aim at extending CNNs to irregular domains, we incorporate the classical settings of CNNs for 2D signals as a particular case of our approach. Designing convolutional layers in the vertex domain directly implies weight sharing, which in other approaches is generally estimated a posteriori using heuristics.

Decentralized Clustering on Compressed Data without Prior Knowledge of the Number of Clusters

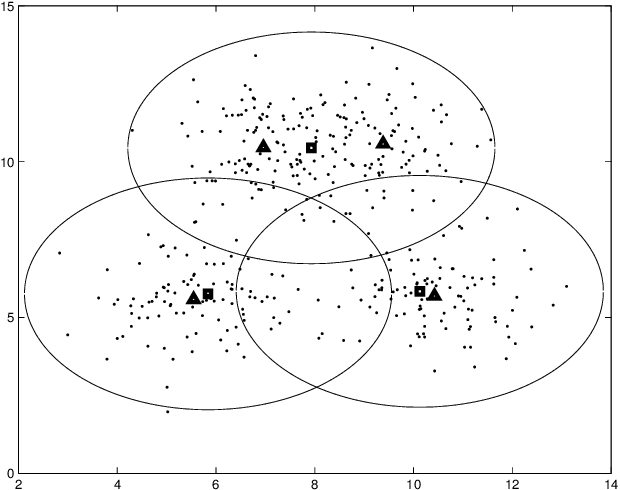
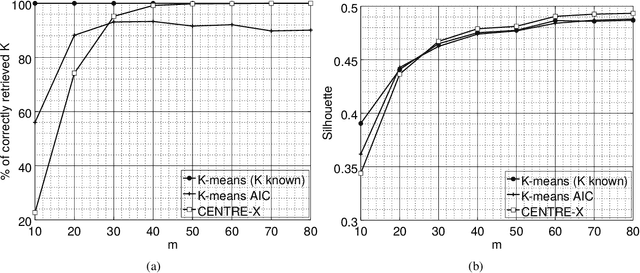
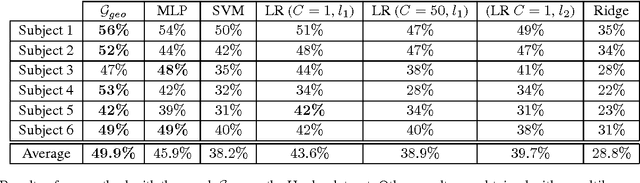
In sensor networks, it is not always practical to set up a fusion center. Therefore, there is need for fully decentralized clustering algorithms. Decentralized clustering algorithms should minimize the amount of data exchanged between sensors in order to reduce sensor energy consumption. In this respect, we propose one centralized and one decentralized clustering algorithm that work on compressed data without prior knowledge of the number of clusters. In the standard K-means clustering algorithm, the number of clusters is estimated by repeating the algorithm several times, which dramatically increases the amount of exchanged data, while our algorithm can estimate this number in one run. The proposed clustering algorithms derive from a theoretical framework establishing that, under asymptotic conditions, the cluster centroids are the only fixed-point of a cost function we introduce. This cost function depends on a weight function which we choose as the p-value of a Wald hypothesis test. This p-value measures the plausibility that a given measurement vector belongs to a given cluster. Experimental results show that our two algorithms are competitive in terms of clustering performance with respect to K-means and DB-Scan, while lowering by a factor at least $2$ the amount of data exchanged between sensors.