Jean-Charles Vialatte
A Unified Deep Learning Formalism For Processing Graph Signals
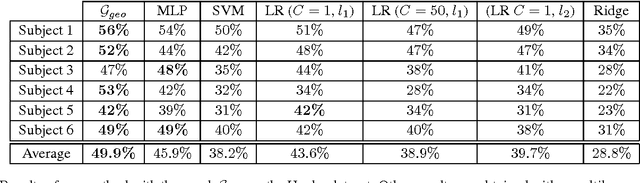
May 01, 2019Abstract:Convolutional Neural Networks are very efficient at processing signals defined on a discrete Euclidean space (such as images). However, as they can not be used on signals defined on an arbitrary graph, other models have emerged, aiming to extend its properties. We propose to review some of the major deep learning models designed to exploit the underlying graph structure of signals. We express them in a unified formalism, giving them a new and comparative reading.
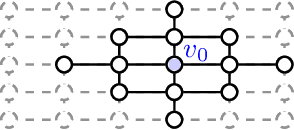
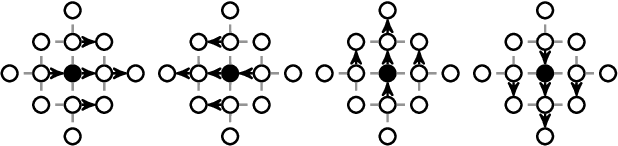
Convolutional neural networks on irregular domains based on approximate vertex-domain translations
Nov 05, 2018
Abstract:We propose a generalization of convolutional neural networks (CNNs) to irregular domains, through the use of a translation operator on a graph structure. In regular settings such as images, convolutional layers are designed by translating a convolutional kernel over all pixels, thus enforcing translation equivariance. In the case of general graphs however, translation is not a well-defined operation, which makes shifting a convolutional kernel not straightforward. In this article, we introduce a methodology to allow the design of convolutional layers that are adapted to signals evolving on irregular topologies, even in the absence of a natural translation. Using the designed layers, we build a CNN that we train using the initial set of signals. Contrary to other approaches that aim at extending CNNs to irregular domains, we incorporate the classical settings of CNNs for 2D signals as a particular case of our approach. Designing convolutional layers in the vertex domain directly implies weight sharing, which in other approaches is generally estimated a posteriori using heuristics.
Matching Convolutional Neural Networks without Priors about Data
Feb 27, 2018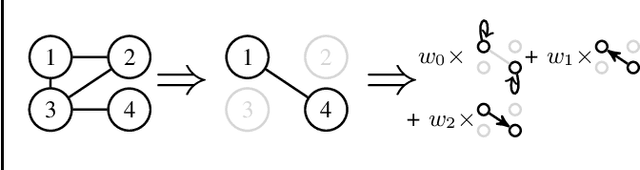
Abstract:We propose an extension of Convolutional Neural Networks (CNNs) to graph-structured data, including strided convolutions and data augmentation on graphs. Our method matches the accuracy of state-of-the-art CNNs when applied on images, without any prior about their 2D regular structure. On fMRI data, we obtain a significant gain in accuracy compared with existing graph-based alternatives.
Generalizing the Convolution Operator to extend CNNs to Irregular Domains
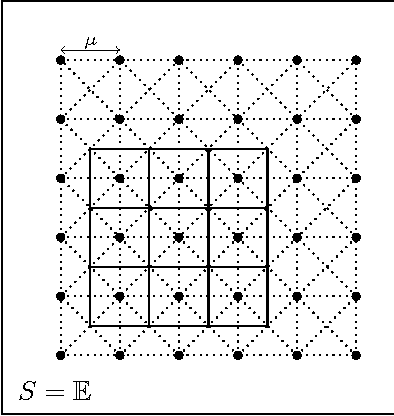
Oct 25, 2017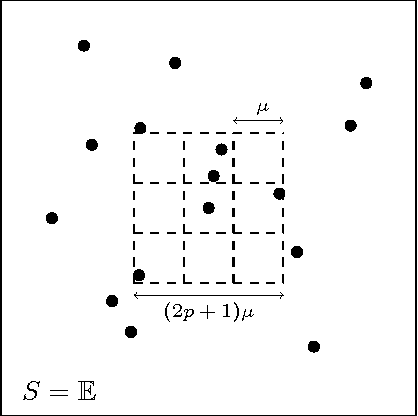
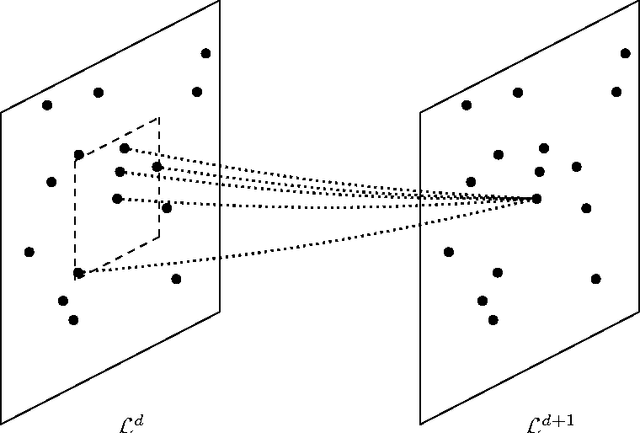
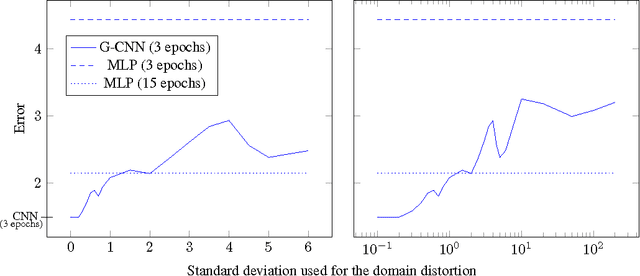
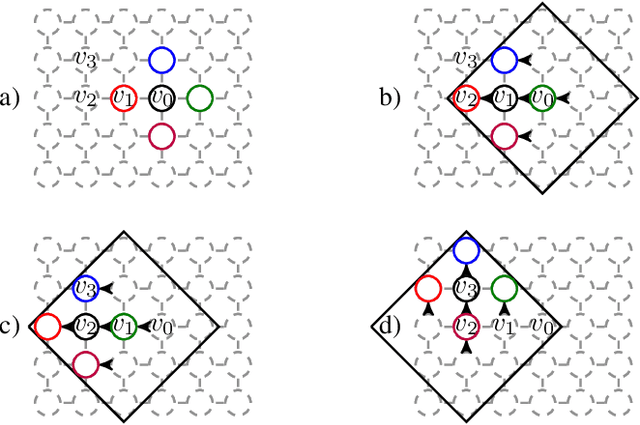
Abstract:Convolutional Neural Networks (CNNs) have become the state-of-the-art in supervised learning vision tasks. Their convolutional filters are of paramount importance for they allow to learn patterns while disregarding their locations in input images. When facing highly irregular domains, generalized convolutional operators based on an underlying graph structure have been proposed. However, these operators do not exactly match standard ones on grid graphs, and introduce unwanted additional invariance (e.g. with regards to rotations). We propose a novel approach to generalize CNNs to irregular domains using weight sharing and graph-based operators. Using experiments, we show that these models resemble CNNs on regular domains and offer better performance than multilayer perceptrons on distorded ones.
Learning Local Receptive Fields and their Weight Sharing Scheme on Graphs
Oct 05, 2017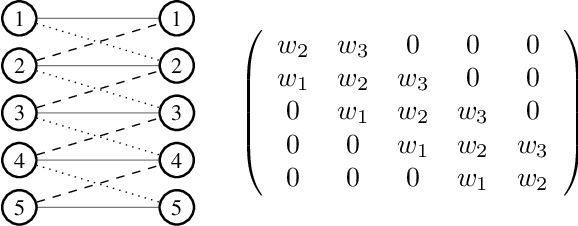
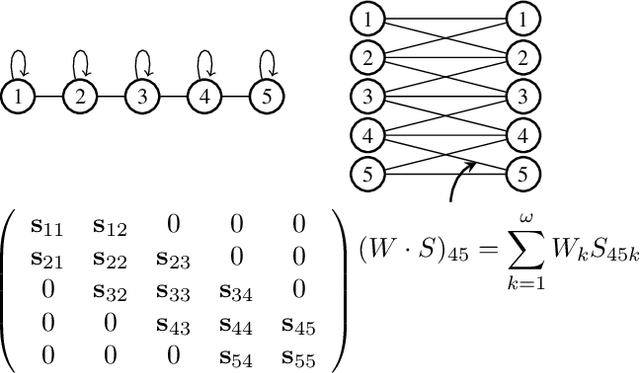
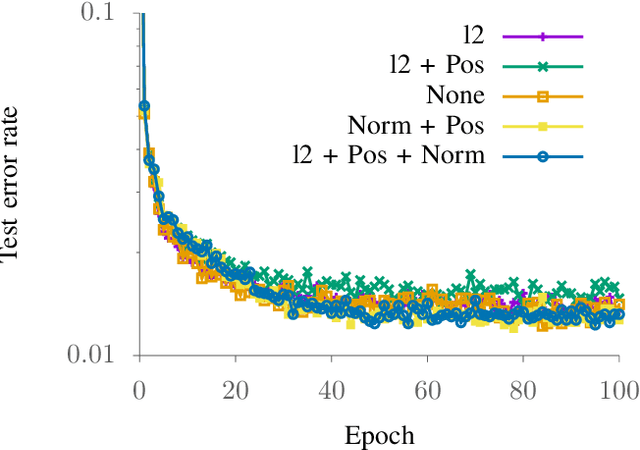
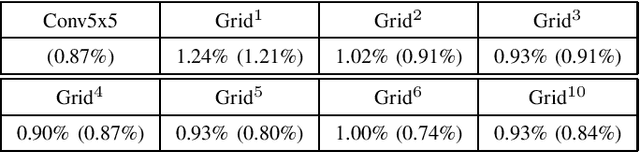
Abstract:We propose a simple and generic layer formulation that extends the properties of convolutional layers to any domain that can be described by a graph. Namely, we use the support of its adjacency matrix to design learnable weight sharing filters able to exploit the underlying structure of signals in the same fashion as for images. The proposed formulation makes it possible to learn the weights of the filter as well as a scheme that controls how they are shared across the graph. We perform validation experiments with image datasets and show that these filters offer performances comparable with convolutional ones.
A Study of Deep Learning Robustness Against Computation Failures
Apr 18, 2017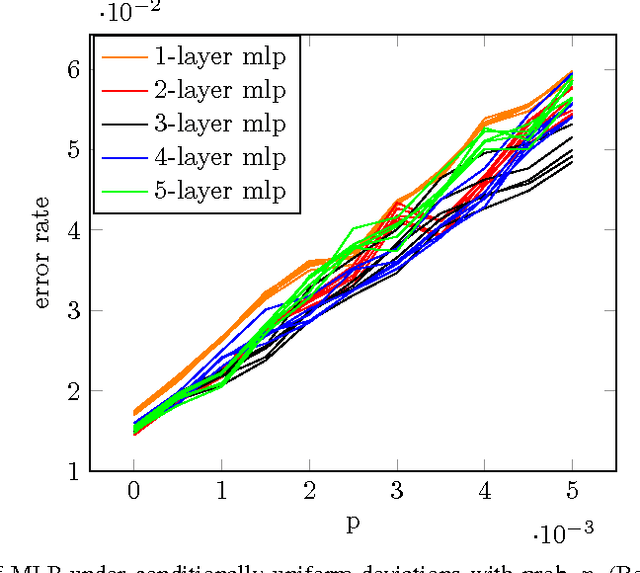
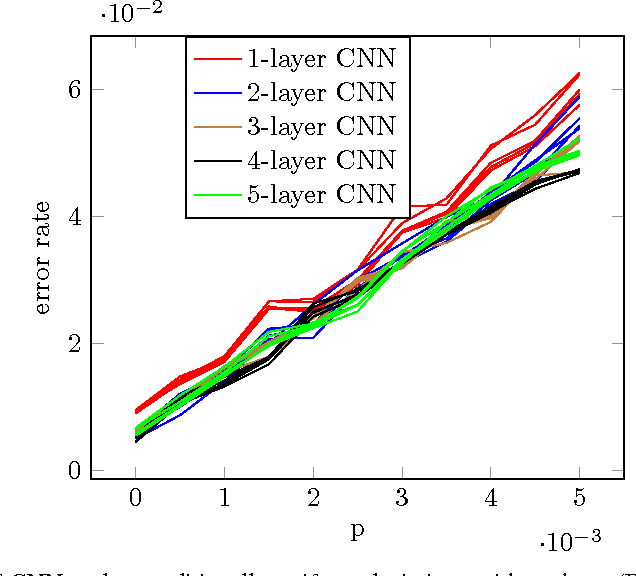
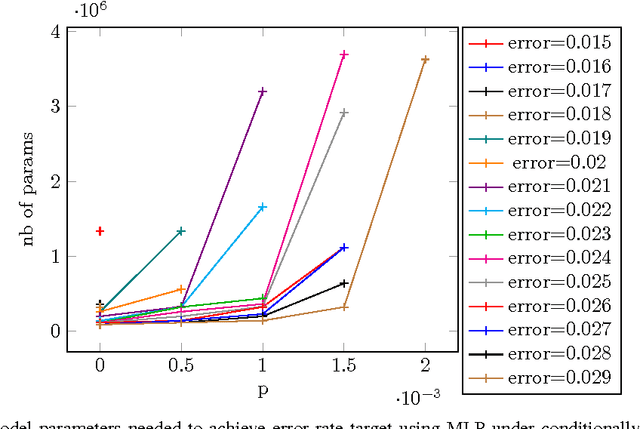
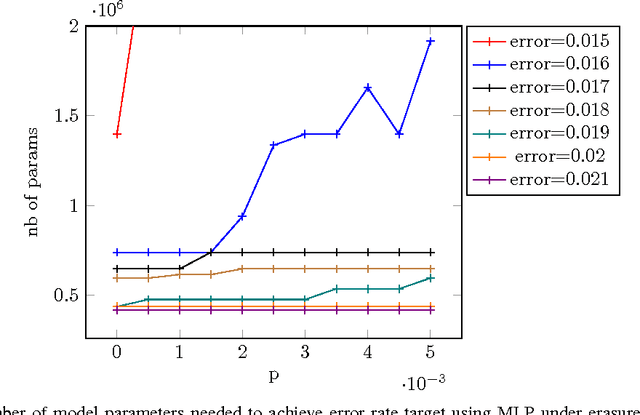
Abstract:For many types of integrated circuits, accepting larger failure rates in computations can be used to improve energy efficiency. We study the performance of faulty implementations of certain deep neural networks based on pessimistic and optimistic models of the effect of hardware faults. After identifying the impact of hyperparameters such as the number of layers on robustness, we study the ability of the network to compensate for computational failures through an increase of the network size. We show that some networks can achieve equivalent performance under faulty implementations, and quantify the required increase in computational complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge