Augmented Invertible Koopman Autoencoder for long-term time series forecasting

Following the introduction of Dynamic Mode Decomposition and its numerous extensions, many neural autoencoder-based implementations of the Koopman operator have recently been proposed. This class of methods appears to be of interest for modeling dynamical systems, either through direct long-term prediction of the evolution of the state or as a powerful embedding for downstream methods. In particular, a recent line of work has developed invertible Koopman autoencoders (IKAEs), which provide an exact reconstruction of the input state thanks to their analytically invertible encoder, based on coupling layer normalizing flow models. We identify that the conservation of the dimension imposed by the normalizing flows is a limitation for the IKAE models, and thus we propose to augment the latent state with a second, non-invertible encoder network. This results in our new model: the Augmented Invertible Koopman AutoEncoder (AIKAE). We demonstrate the relevance of the AIKAE through a series of long-term time series forecasting experiments, on satellite image time series as well as on a benchmark involving predictions based on a large lookback window of observations.

MemSE: Fast MSE Prediction for Noisy Memristor-Based DNN Accelerators

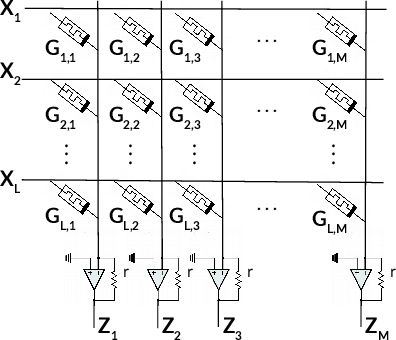
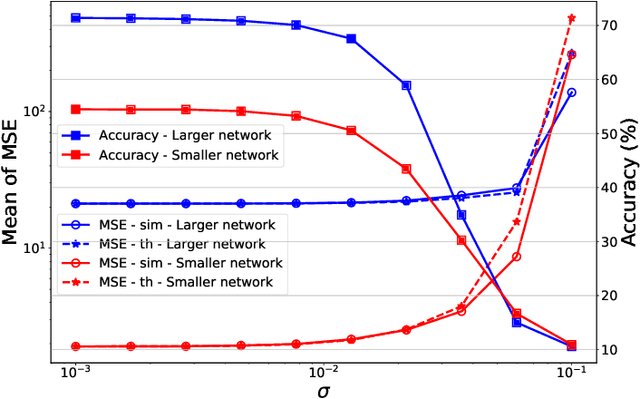
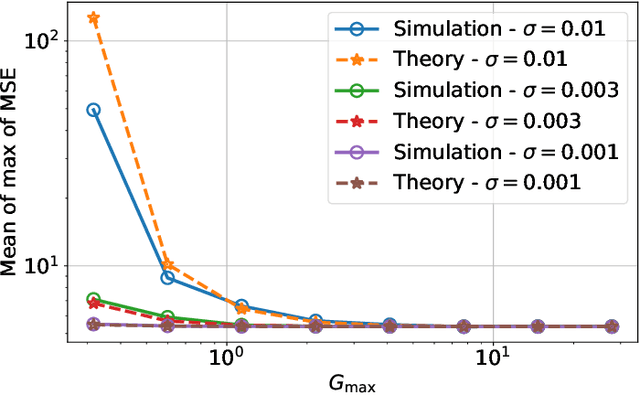
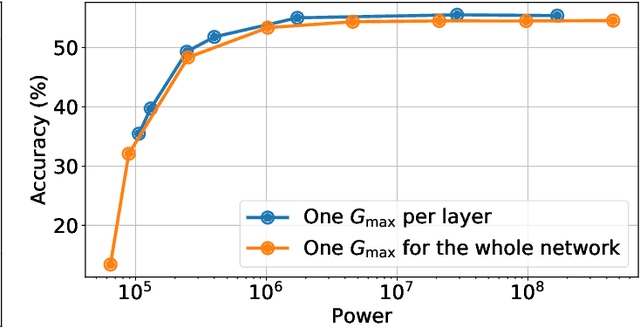
Memristors enable the computation of matrix-vector multiplications (MVM) in memory and, therefore, show great potential in highly increasing the energy efficiency of deep neural network (DNN) inference accelerators. However, computations in memristors suffer from hardware non-idealities and are subject to different sources of noise that may negatively impact system performance. In this work, we theoretically analyze the mean squared error of DNNs that use memristor crossbars to compute MVM. We take into account both the quantization noise, due to the necessity of reducing the DNN model size, and the programming noise, stemming from the variability during the programming of the memristance value. Simulations on pre-trained DNN models showcase the accuracy of the analytical prediction. Furthermore the proposed method is almost two order of magnitude faster than Monte-Carlo simulation, thus making it possible to optimize the implementation parameters to achieve minimal error for a given power constraint.

Optimizing the Energy Efficiency of Unreliable Memories for Quantized Kalman Filtering

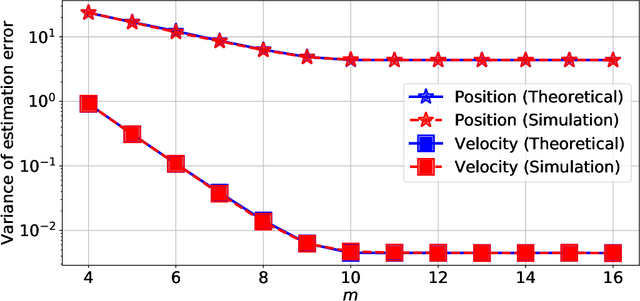
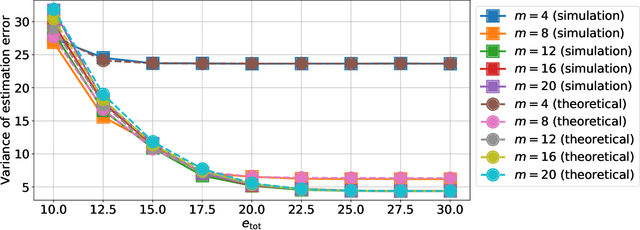
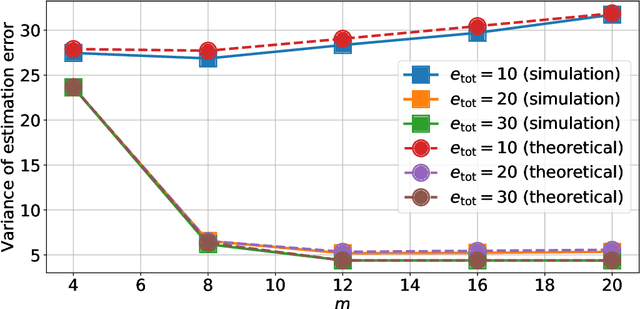
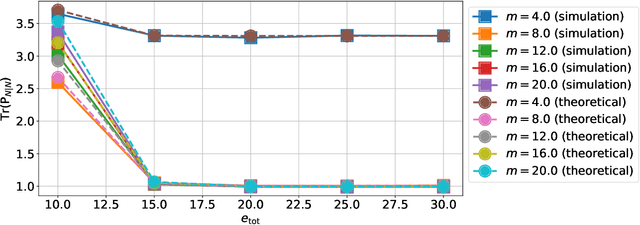
This paper presents a quantized Kalman filter implemented using unreliable memories. We consider that both the quantization and the unreliable memories introduce errors in the computations, and develop an error propagation model that takes into account these two sources of errors. In addition to providing updated Kalman filter equations, the proposed error model accurately predicts the covariance of the estimation error and gives a relation between the performance of the filter and its energy consumption, depending on the noise level in the memories. Then, since memories are responsible for a large part of the energy consumption of embedded systems, optimization methods are introduced so as to minimize the memory energy consumption under a desired estimation performance of the filter. The first method computes the optimal energy levels allocated to each memory bank individually, and the second one optimizes the energy allocation per groups of memory banks. Simulations show a close match between the theoretical analysis and experimental results. Furthermore, they demonstrate an important reduction in energy consumption of more than 50%.

Locally-adapted convolution-based super-resolution of irregularly-sampled ocean remote sensing data

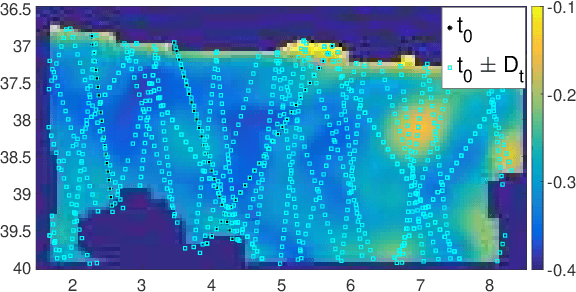
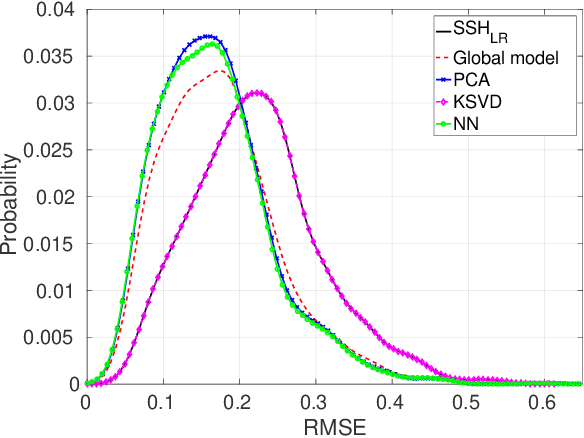
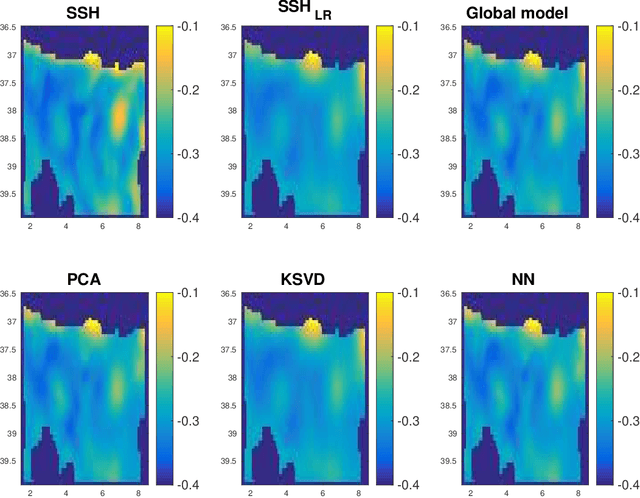
Super-resolution is a classical problem in image processing, with numerous applications to remote sensing image enhancement. Here, we address the super-resolution of irregularly-sampled remote sensing images. Using an optimal interpolation as the low-resolution reconstruction, we explore locally-adapted multimodal convolutional models and investigate different dictionary-based decompositions, namely based on principal component analysis (PCA), sparse priors and non-negativity constraints. We consider an application to the reconstruction of sea surface height (SSH) fields from two information sources, along-track altimeter data and sea surface temperature (SST) data. The reported experiments demonstrate the relevance of the proposed model, especially locally-adapted parametrizations with non-negativity constraints, to outperform optimally-interpolated reconstructions.