Koopman Ensembles for Probabilistic Time Series Forecasting

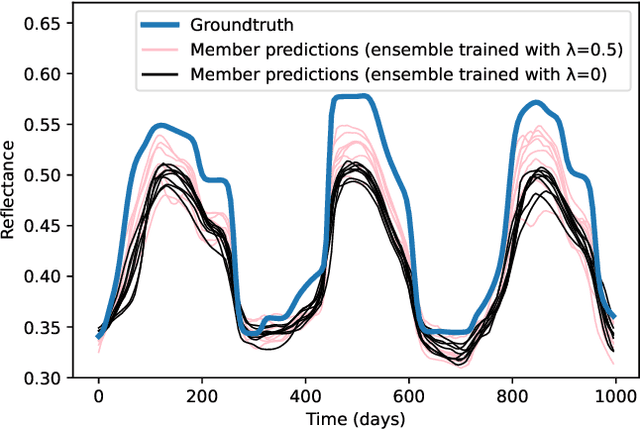
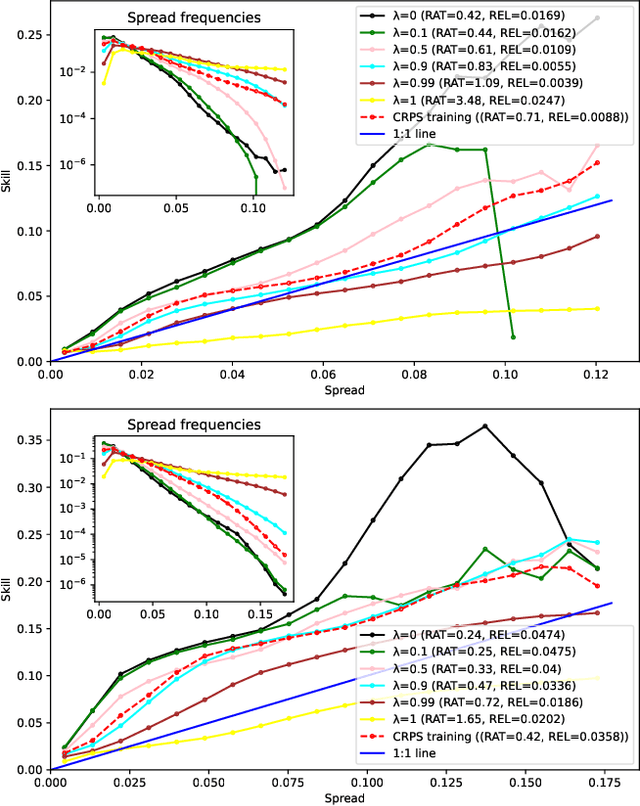
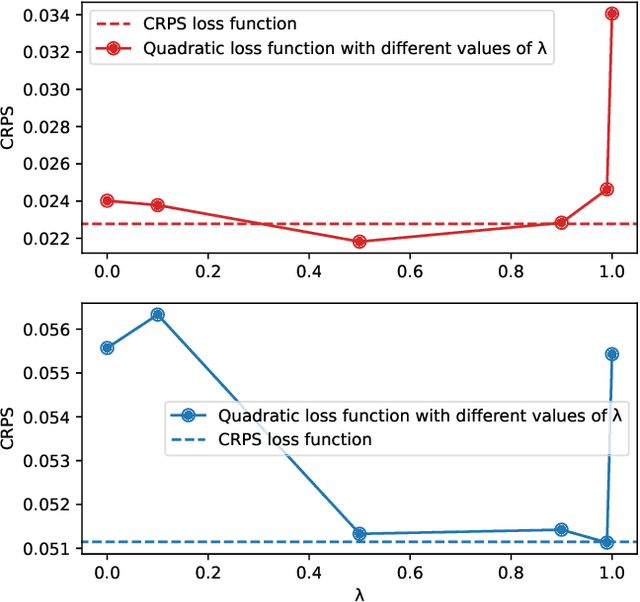
In the context of an increasing popularity of data-driven models to represent dynamical systems, many machine learning-based implementations of the Koopman operator have recently been proposed. However, the vast majority of those works are limited to deterministic predictions, while the knowledge of uncertainty is critical in fields like meteorology and climatology. In this work, we investigate the training of ensembles of models to produce stochastic outputs. We show through experiments on real remote sensing image time series that ensembles of independently trained models are highly overconfident and that using a training criterion that explicitly encourages the members to produce predictions with high inter-model variances greatly improves the uncertainty quantification of the ensembles.

Neural Koopman prior for data assimilation

With the increasing availability of large scale datasets, computational power and tools like automatic differentiation and expressive neural network architectures, sequential data are now often treated in a data-driven way, with a dynamical model trained from the observation data. While neural networks are often seen as uninterpretable black-box architectures, they can still benefit from physical priors on the data and from mathematical knowledge. In this paper, we use a neural network architecture which leverages the long-known Koopman operator theory to embed dynamical systems in latent spaces where their dynamics can be described linearly, enabling a number of appealing features. We introduce methods that enable to train such a model for long-term continuous reconstruction, even in difficult contexts where the data comes in irregularly-sampled time series. The potential for self-supervised learning is also demonstrated, as we show the promising use of trained dynamical models as priors for variational data assimilation techniques, with applications to e.g. time series interpolation and forecasting.

Learning Sentinel-2 reflectance dynamics for data-driven assimilation and forecasting

Over the last few years, massive amounts of satellite multispectral and hyperspectral images covering the Earth's surface have been made publicly available for scientific purpose, for example through the European Copernicus project. Simultaneously, the development of self-supervised learning (SSL) methods has sparked great interest in the remote sensing community, enabling to learn latent representations from unlabeled data to help treating downstream tasks for which there is few annotated examples, such as interpolation, forecasting or unmixing. Following this line, we train a deep learning model inspired from the Koopman operator theory to model long-term reflectance dynamics in an unsupervised way. We show that this trained model, being differentiable, can be used as a prior for data assimilation in a straightforward way. Our datasets, which are composed of Sentinel-2 multispectral image time series, are publicly released with several levels of treatment.

Leveraging Neural Koopman Operators to Learn Continuous Representations of Dynamical Systems from Scarce Data

Over the last few years, several works have proposed deep learning architectures to learn dynamical systems from observation data with no or little knowledge of the underlying physics. A line of work relies on learning representations where the dynamics of the underlying phenomenon can be described by a linear operator, based on the Koopman operator theory. However, despite being able to provide reliable long-term predictions for some dynamical systems in ideal situations, the methods proposed so far have limitations, such as requiring to discretize intrinsically continuous dynamical systems, leading to data loss, especially when handling incomplete or sparsely sampled data. Here, we propose a new deep Koopman framework that represents dynamics in an intrinsically continuous way, leading to better performance on limited training data, as exemplified on several datasets arising from dynamical systems.