MemSE: Fast MSE Prediction for Noisy Memristor-Based DNN Accelerators
Paper and Code
May 03, 2022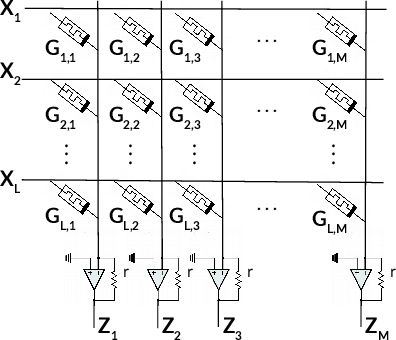
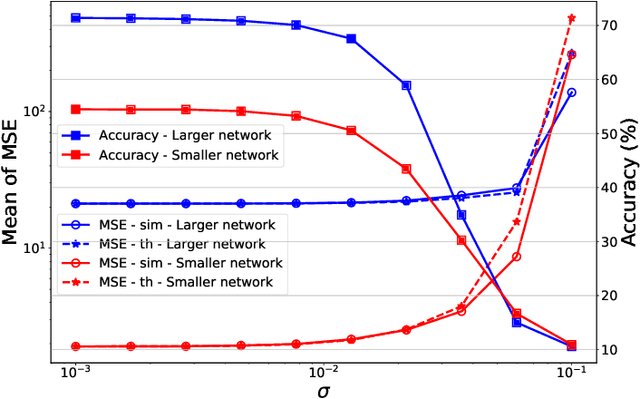
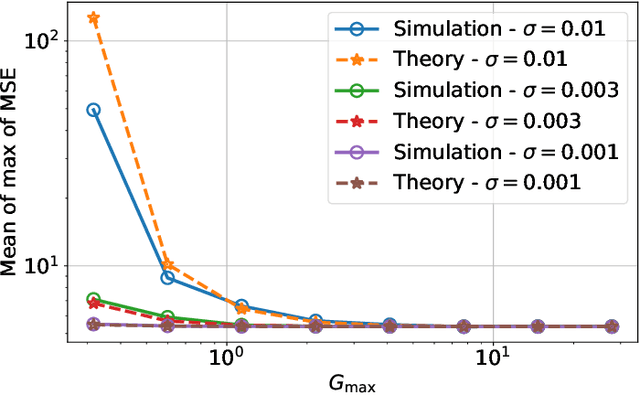
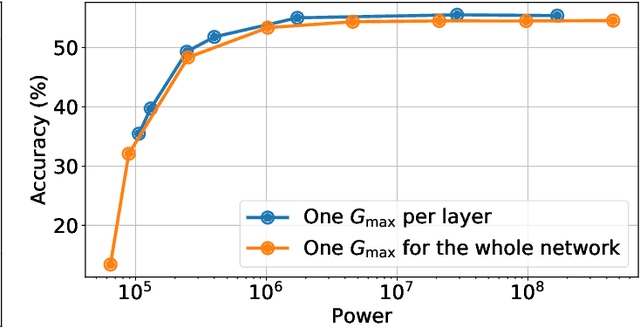
Memristors enable the computation of matrix-vector multiplications (MVM) in memory and, therefore, show great potential in highly increasing the energy efficiency of deep neural network (DNN) inference accelerators. However, computations in memristors suffer from hardware non-idealities and are subject to different sources of noise that may negatively impact system performance. In this work, we theoretically analyze the mean squared error of DNNs that use memristor crossbars to compute MVM. We take into account both the quantization noise, due to the necessity of reducing the DNN model size, and the programming noise, stemming from the variability during the programming of the memristance value. Simulations on pre-trained DNN models showcase the accuracy of the analytical prediction. Furthermore the proposed method is almost two order of magnitude faster than Monte-Carlo simulation, thus making it possible to optimize the implementation parameters to achieve minimal error for a given power constraint.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge