Stephan Wojtowytsch
Momentum-based minimization of the Ginzburg-Landau functional on Euclidean spaces and graphs
Dec 31, 2024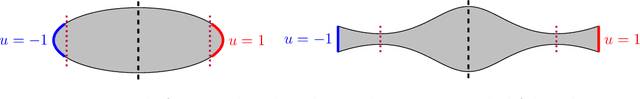

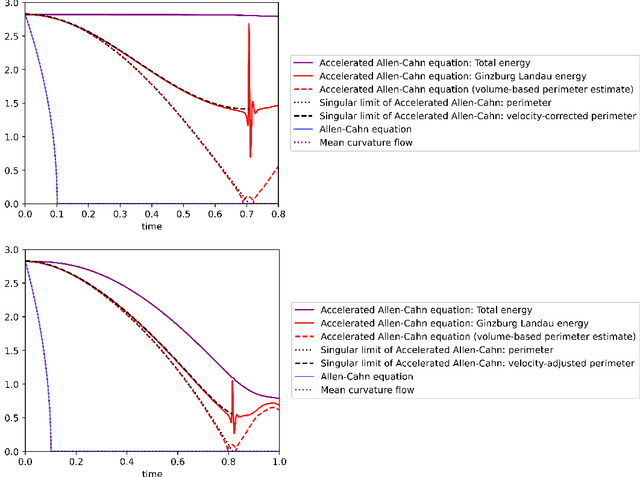
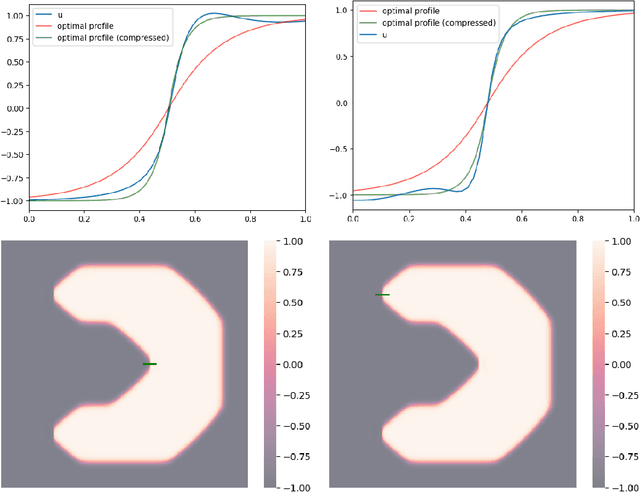
Abstract:We study the momentum-based minimization of a diffuse perimeter functional on Euclidean spaces and on graphs with applications to semi-supervised classification tasks in machine learning. While the gradient flow in the task at hand is a parabolic partial differential equation, the momentum-method corresponds to a damped hyperbolic PDE, leading to qualitatively and quantitatively different trajectories. Using a convex-concave splitting-based FISTA-type time discretization, we demonstrate empirically that momentum can lead to faster convergence if the time step size is large but not too large. With large time steps, the PDE analysis offers only limited insight into the geometric behavior of solutions and typical hyperbolic phenomena like loss of regularity are not be observed in sample simulations.
Solving the Poisson Equation with Dirichlet data by shallow ReLU$^α$-networks: A regularity and approximation perspective
Dec 10, 2024Abstract:For several classes of neural PDE solvers (Deep Ritz, PINNs, DeepONets), the ability to approximate the solution or solution operator to a partial differential equation (PDE) hinges on the abilitiy of a neural network to approximate the solution in the spatial variables. We analyze the capacity of neural networks to approximate solutions to an elliptic PDE assuming that the boundary condition can be approximated efficiently. Our focus is on the Laplace operator with Dirichlet boundary condition on a half space and on neural networks with a single hidden layer and an activation function that is a power of the popular ReLU activation function.
Nesterov acceleration in benignly non-convex landscapes
Oct 10, 2024Abstract:While momentum-based optimization algorithms are commonly used in the notoriously non-convex optimization problems of deep learning, their analysis has historically been restricted to the convex and strongly convex setting. In this article, we partially close this gap between theory and practice and demonstrate that virtually identical guarantees can be obtained in optimization problems with a `benign' non-convexity. We show that these weaker geometric assumptions are well justified in overparametrized deep learning, at least locally. Variations of this result are obtained for a continuous time model of Nesterov's accelerated gradient descent algorithm (NAG), the classical discrete time version of NAG, and versions of NAG with stochastic gradient estimates with purely additive noise and with noise that exhibits both additive and multiplicative scaling.
SineNet: Learning Temporal Dynamics in Time-Dependent Partial Differential Equations
Mar 28, 2024



Abstract:We consider using deep neural networks to solve time-dependent partial differential equations (PDEs), where multi-scale processing is crucial for modeling complex, time-evolving dynamics. While the U-Net architecture with skip connections is commonly used by prior studies to enable multi-scale processing, our analysis shows that the need for features to evolve across layers results in temporally misaligned features in skip connections, which limits the model's performance. To address this limitation, we propose SineNet, consisting of multiple sequentially connected U-shaped network blocks, referred to as waves. In SineNet, high-resolution features are evolved progressively through multiple stages, thereby reducing the amount of misalignment within each stage. We furthermore analyze the role of skip connections in enabling both parallel and sequential processing of multi-scale information. Our method is rigorously tested on multiple PDE datasets, including the Navier-Stokes equations and shallow water equations, showcasing the advantages of our proposed approach over conventional U-Nets with a comparable parameter budget. We further demonstrate that increasing the number of waves in SineNet while maintaining the same number of parameters leads to a monotonically improved performance. The results highlight the effectiveness of SineNet and the potential of our approach in advancing the state-of-the-art in neural PDE solver design. Our code is available as part of AIRS (https://github.com/divelab/AIRS).
Minimum norm interpolation by perceptra: Explicit regularization and implicit bias
Nov 10, 2023Abstract:We investigate how shallow ReLU networks interpolate between known regions. Our analysis shows that empirical risk minimizers converge to a minimum norm interpolant as the number of data points and parameters tends to infinity when a weight decay regularizer is penalized with a coefficient which vanishes at a precise rate as the network width and the number of data points grow. With and without explicit regularization, we numerically study the implicit bias of common optimization algorithms towards known minimum norm interpolants.
A qualitative difference between gradient flows of convex functions in finite- and infinite-dimensional Hilbert spaces
Oct 26, 2023Abstract:We consider gradient flow/gradient descent and heavy ball/accelerated gradient descent optimization for convex objective functions. In the gradient flow case, we prove the following: 1. If $f$ does not have a minimizer, the convergence $f(x_t)\to \inf f$ can be arbitrarily slow. 2. If $f$ does have a minimizer, the excess energy $f(x_t) - \inf f$ is integrable/summable in time. In particular, $f(x_t) - \inf f = o(1/t)$ as $t\to\infty$. 3. In Hilbert spaces, this is optimal: $f(x_t) - \inf f$ can decay to $0$ as slowly as any given function which is monotone decreasing and integrable at $\infty$, even for a fixed quadratic objective. 4. In finite dimension (or more generally, for all gradient flow curves of finite length), this is not optimal: We prove that there are convex monotone decreasing integrable functions $g(t)$ which decrease to zero slower than $f(x_t)-\inf f$ for the gradient flow of any convex function on $\mathbb R^d$. For instance, we show that any gradient flow $x_t$ of a convex function $f$ in finite dimension satisfies $\liminf_{t\to\infty} \big(t\cdot \log^2(t)\cdot \big\{f(x_t) -\inf f\big\}\big)=0$. This improves on the commonly reported $O(1/t)$ rate and provides a sharp characterization of the energy decay law. We also note that it is impossible to establish a rate $O(1/(t\phi(t))$ for any function $\phi$ which satisfies $\lim_{t\to\infty}\phi(t) = \infty$, even asymptotically. Similar results are obtained in related settings for (1) discrete time gradient descent, (2) stochastic gradient descent with multiplicative noise and (3) the heavy ball ODE. In the case of stochastic gradient descent, the summability of $\mathbb E[f(x_n) - \inf f]$ is used to prove that $f(x_n)\to \inf f$ almost surely - an improvement on the convergence almost surely up to a subsequence which follows from the $O(1/n)$ decay estimate.
Group Equivariant Fourier Neural Operators for Partial Differential Equations
Jun 09, 2023
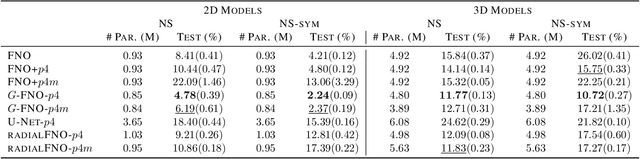


Abstract:We consider solving partial differential equations (PDEs) with Fourier neural operators (FNOs), which operate in the frequency domain. Since the laws of physics do not depend on the coordinate system used to describe them, it is desirable to encode such symmetries in the neural operator architecture for better performance and easier learning. While encoding symmetries in the physical domain using group theory has been studied extensively, how to capture symmetries in the frequency domain is under-explored. In this work, we extend group convolutions to the frequency domain and design Fourier layers that are equivariant to rotations, translations, and reflections by leveraging the equivariance property of the Fourier transform. The resulting $G$-FNO architecture generalizes well across input resolutions and performs well in settings with varying levels of symmetry. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS).
Achieving acceleration despite very noisy gradients
Feb 10, 2023Abstract:We present a novel momentum-based first order optimization method (AGNES) which provably achieves acceleration for convex minimization, even if the stochastic noise in the gradient estimates is many orders of magnitude larger than the gradient itself. Here we model the noise as having a variance which is proportional to the magnitude of the underlying gradient. We argue, based upon empirical evidence, that this is appropriate for mini-batch gradients in overparameterized deep learning. Furthermore, we demonstrate that the method achieves competitive performance in the training of CNNs on MNIST and CIFAR-10.
Optimal bump functions for shallow ReLU networks: Weight decay, depth separation and the curse of dimensionality
Sep 02, 2022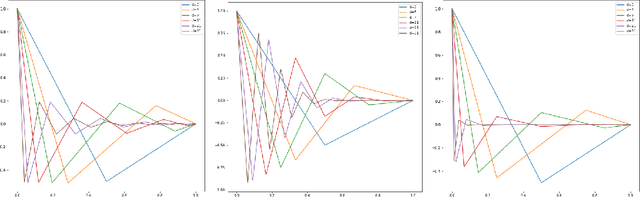
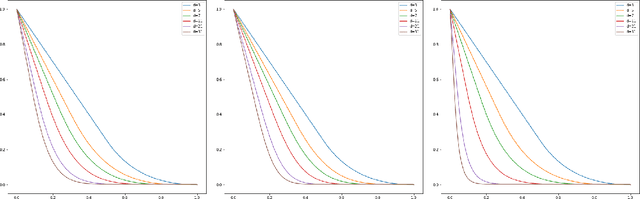
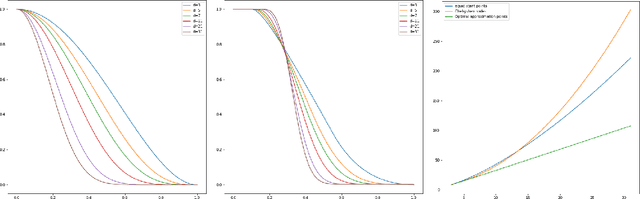
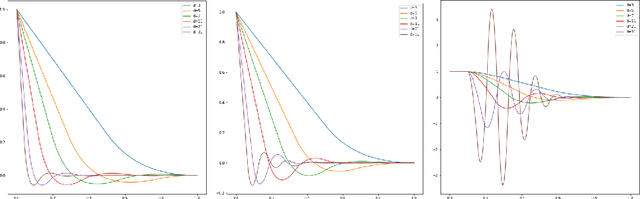
Abstract:In this note, we study how neural networks with a single hidden layer and ReLU activation interpolate data drawn from a radially symmetric distribution with target labels 1 at the origin and 0 outside the unit ball, if no labels are known inside the unit ball. With weight decay regularization and in the infinite neuron, infinite data limit, we prove that a unique radially symmetric minimizer exists, whose weight decay regularizer and Lipschitz constant grow as $d$ and $\sqrt{d}$ respectively. We furthermore show that the weight decay regularizer grows exponentially in $d$ if the label $1$ is imposed on a ball of radius $\varepsilon$ rather than just at the origin. By comparison, a neural networks with two hidden layers can approximate the target function without encountering the curse of dimensionality.
Qualitative neural network approximation over R and C: Elementary proofs for analytic and polynomial activation
Mar 25, 2022Abstract:In this article, we prove approximation theorems in classes of deep and shallow neural networks with analytic activation functions by elementary arguments. We prove for both real and complex networks with non-polynomial activation that the closure of the class of neural networks coincides with the closure of the space of polynomials. The closure can further be characterized by the Stone-Weierstrass theorem (in the real case) and Mergelyan's theorem (in the complex case). In the real case, we further prove approximation results for networks with higher-dimensional harmonic activation and orthogonally projected linear maps. We further show that fully connected and residual networks of large depth with polynomial activation functions can approximate any polynomial under certain width requirements. All proofs are entirely elementary.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge