Qualitative neural network approximation over R and C: Elementary proofs for analytic and polynomial activation

In this article, we prove approximation theorems in classes of deep and shallow neural networks with analytic activation functions by elementary arguments. We prove for both real and complex networks with non-polynomial activation that the closure of the class of neural networks coincides with the closure of the space of polynomials. The closure can further be characterized by the Stone-Weierstrass theorem (in the real case) and Mergelyan's theorem (in the complex case). In the real case, we further prove approximation results for networks with higher-dimensional harmonic activation and orthogonally projected linear maps. We further show that fully connected and residual networks of large depth with polynomial activation functions can approximate any polynomial under certain width requirements. All proofs are entirely elementary.

Neural Network Approximation of Refinable Functions

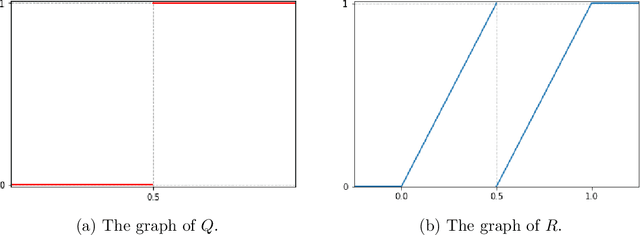
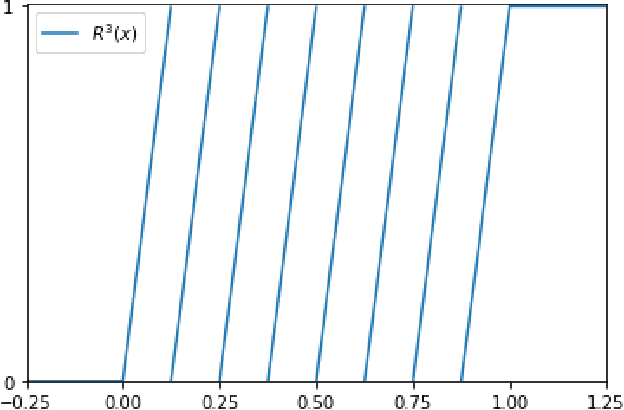
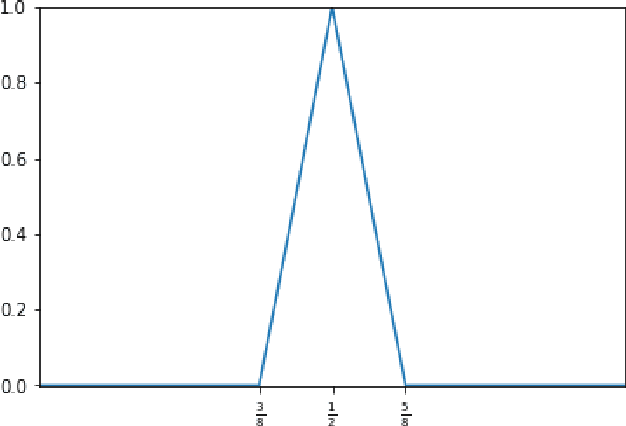
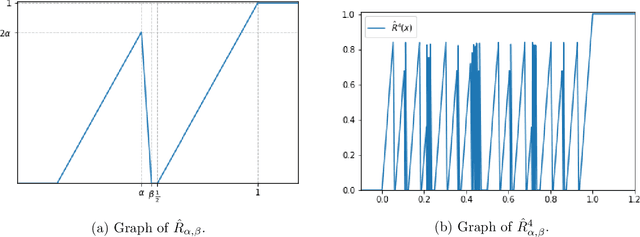
In the desire to quantify the success of neural networks in deep learning and other applications, there is a great interest in understanding which functions are efficiently approximated by the outputs of neural networks. By now, there exists a variety of results which show that a wide range of functions can be approximated with sometimes surprising accuracy by these outputs. For example, it is known that the set of functions that can be approximated with exponential accuracy (in terms of the number of parameters used) includes, on one hand, very smooth functions such as polynomials and analytic functions (see e.g. \cite{E,S,Y}) and, on the other hand, very rough functions such as the Weierstrass function (see e.g. \cite{EPGB,DDFHP}), which is nowhere differentiable. In this paper, we add to the latter class of rough functions by showing that it also includes refinable functions. Namely, we show that refinable functions are approximated by the outputs of deep ReLU networks with a fixed width and increasing depth with accuracy exponential in terms of their number of parameters. Our results apply to functions used in the standard construction of wavelets as well as to functions constructed via subdivision algorithms in Computer Aided Geometric Design.