Critical biblical studies via word frequency analysis: unveiling text authorship

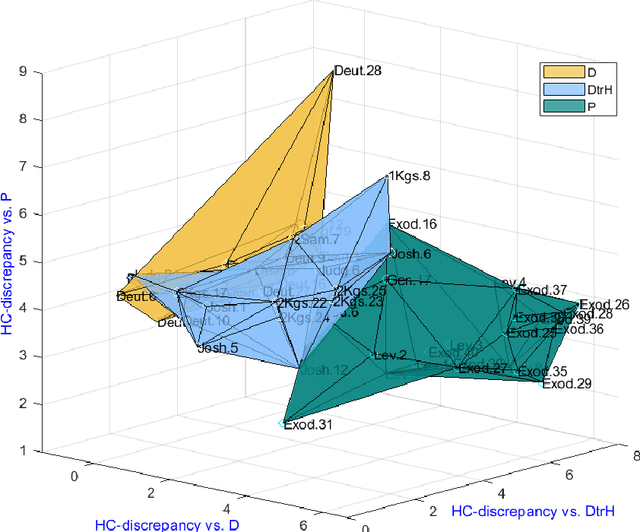
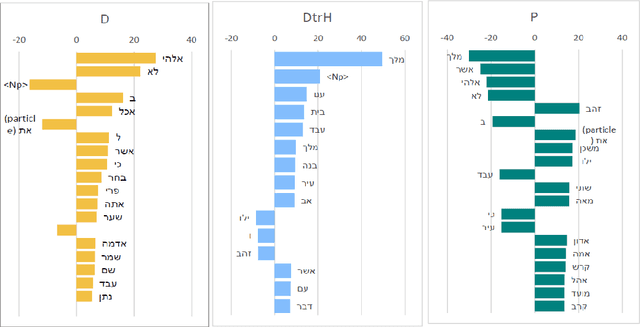
The Bible, a product of an extensive and intricate process of oral-written transmission spanning centuries, obscures the contours of its earlier recensions. Debate rages over determining the existing layers and identifying the date of composition and historical background of the biblical texts. Traditional manual methodologies have grappled with authorship challenges through scrupulous textual criticism, employing linguistic, stylistic, inner-biblical, and historical criteria. Despite recent progress in computer-assisted analysis, many patterns still need to be uncovered in Biblical Texts. In this study, we address the question of authorship of biblical texts by employing statistical analysis to the frequency of words using a method that is particularly sensitive to deviations in frequencies associated with a few words out of potentially many. We aim to differentiate between three distinct authors across numerous chapters spanning the first nine books of the Bible. In particular, we examine 50 chapters labeled according to biblical exegesis considerations into three corpora (D, DtrH, and P). Without prior assumptions about author identity, our approach leverages subtle differences in word frequencies to distinguish among the three corpora and identify author-dependent linguistic properties. Our analysis indicates that the first two authors (D and DtrH) are much more closely related compared to P, a fact that aligns with expert assessments. Additionally, we attain high accuracy in attributing authorship by evaluating the similarity of each chapter with the reference corpora. This study sheds new light on the authorship of biblical texts by providing interpretable, statistically significant evidence that there are different linguistic characteristics of biblical authors and that these differences can be identified.

Image Quality Assessment: Learning to Rank Image Distortion Level

Over the years, various algorithms were developed, attempting to imitate the Human Visual System (HVS), and evaluate the perceptual image quality. However, for certain image distortions, the functionality of the HVS continues to be an enigma, and echoing its behavior remains a challenge (especially for ill-defined distortions). In this paper, we learn to compare the image quality of two registered images, with respect to a chosen distortion. Our method takes advantage of the fact that at times, simulating image distortion and later evaluating its relative image quality, is easier than assessing its absolute value. Thus, given a pair of images, we look for an optimal dimensional reduction function that will map each image to a numerical score, so that the scores will reflect the image quality relation (i.e., a less distorted image will receive a lower score). We look for an optimal dimensional reduction mapping in the form of a Deep Neural Network which minimizes the violation of image quality order. Subsequently, we extend the method to order a set of images by utilizing the predicted level of the chosen distortion. We demonstrate the validity of our method on Latent Chromatic Aberration and Moire distortions, on synthetic and real datasets.

Neural Network Approximation of Refinable Functions

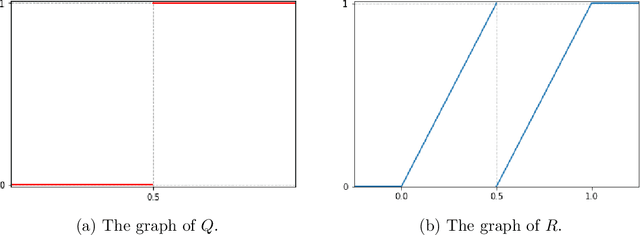
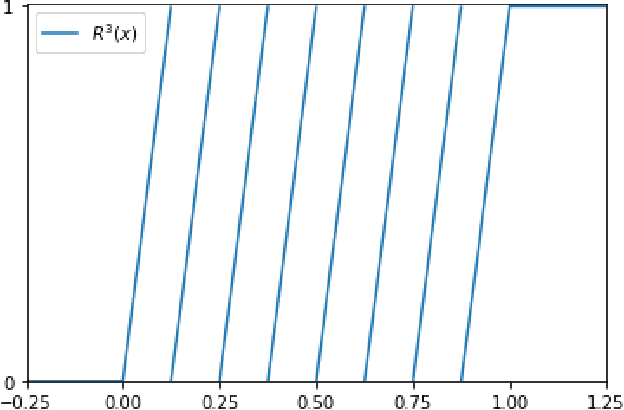
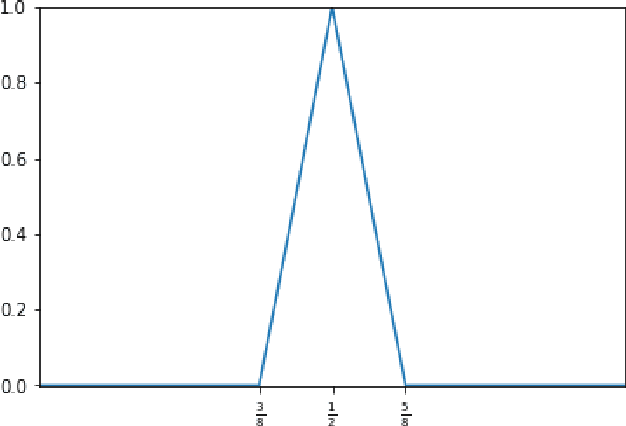
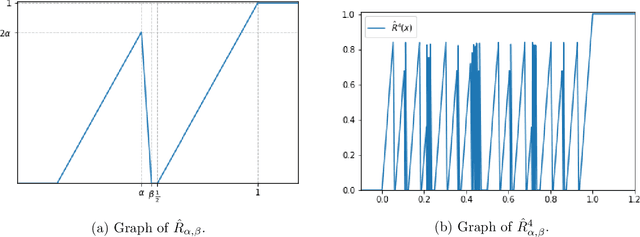
In the desire to quantify the success of neural networks in deep learning and other applications, there is a great interest in understanding which functions are efficiently approximated by the outputs of neural networks. By now, there exists a variety of results which show that a wide range of functions can be approximated with sometimes surprising accuracy by these outputs. For example, it is known that the set of functions that can be approximated with exponential accuracy (in terms of the number of parameters used) includes, on one hand, very smooth functions such as polynomials and analytic functions (see e.g. \cite{E,S,Y}) and, on the other hand, very rough functions such as the Weierstrass function (see e.g. \cite{EPGB,DDFHP}), which is nowhere differentiable. In this paper, we add to the latter class of rough functions by showing that it also includes refinable functions. Namely, we show that refinable functions are approximated by the outputs of deep ReLU networks with a fixed width and increasing depth with accuracy exponential in terms of their number of parameters. Our results apply to functions used in the standard construction of wavelets as well as to functions constructed via subdivision algorithms in Computer Aided Geometric Design.