Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

Group Equivariant Fourier Neural Operators for Partial Differential Equations

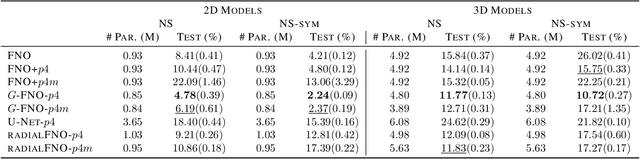
We consider solving partial differential equations (PDEs) with Fourier neural operators (FNOs), which operate in the frequency domain. Since the laws of physics do not depend on the coordinate system used to describe them, it is desirable to encode such symmetries in the neural operator architecture for better performance and easier learning. While encoding symmetries in the physical domain using group theory has been studied extensively, how to capture symmetries in the frequency domain is under-explored. In this work, we extend group convolutions to the frequency domain and design Fourier layers that are equivariant to rotations, translations, and reflections by leveraging the equivariance property of the Fourier transform. The resulting $G$-FNO architecture generalizes well across input resolutions and performs well in settings with varying levels of symmetry. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS).

Learning Protein Representations via Complete 3D Graph Networks

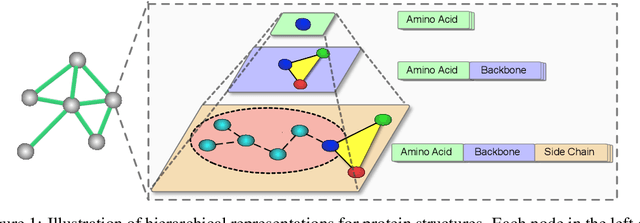
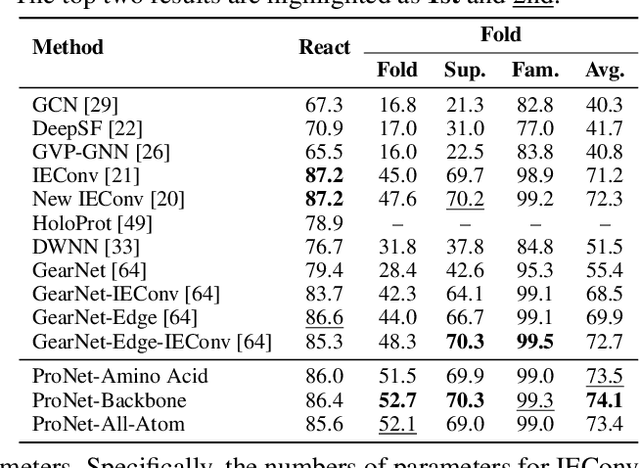
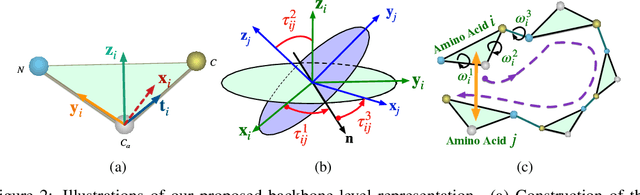
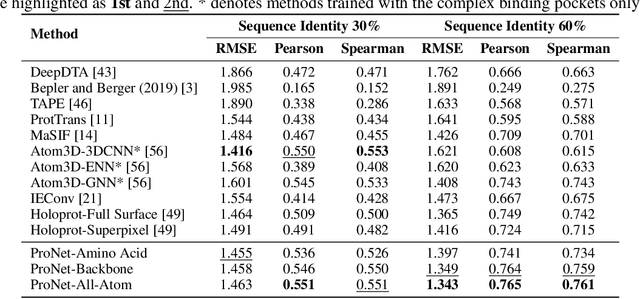
We consider representation learning for proteins with 3D structures. We build 3D graphs based on protein structures and develop graph networks to learn their representations. Depending on the levels of details that we wish to capture, protein representations can be computed at different levels, \emph{e.g.}, the amino acid, backbone, or all-atom levels. Importantly, there exist hierarchical relations among different levels. In this work, we propose to develop a novel hierarchical graph network, known as ProNet, to capture the relations. Our ProNet is very flexible and can be used to compute protein representations at different levels of granularity. We show that, given a base 3D graph network that is complete, our ProNet representations are also complete at all levels. To close the loop, we develop a complete and efficient 3D graph network to be used as a base model, making our ProNet complete. We conduct experiments on multiple downstream tasks. Results show that ProNet outperforms recent methods on most datasets. In addition, results indicate that different downstream tasks may require representations at different levels. Our code is available as part of the DIG library (\url{https://github.com/divelab/DIG}).