An extrapolated and provably convergent algorithm for nonlinear matrix decomposition with the ReLU function

Nonlinear matrix decomposition (NMD) with the ReLU function, denoted ReLU-NMD, is the following problem: given a sparse, nonnegative matrix $X$ and a factorization rank $r$, identify a rank-$r$ matrix $\Theta$ such that $X\approx \max(0,\Theta)$. This decomposition finds application in data compression, matrix completion with entries missing not at random, and manifold learning. The standard ReLU-NMD model minimizes the least squares error, that is, $\|X - \max(0,\Theta)\|_F^2$. The corresponding optimization problem is nondifferentiable and highly nonconvex. This motivated Saul to propose an alternative model, Latent-ReLU-NMD, where a latent variable $Z$ is introduced and satisfies $\max(0,Z)=X$ while minimizing $\|Z - \Theta\|_F^2$ (``A nonlinear matrix decomposition for mining the zeros of sparse data'', SIAM J. Math. Data Sci., 2022). Our first contribution is to show that the two formulations may yield different low-rank solutions $\Theta$; in particular, we show that Latent-ReLU-NMD can be ill-posed when ReLU-NMD is not, meaning that there are instances in which the infimum of Latent-ReLU-NMD is not attained while that of ReLU-NMD is. We also consider another alternative model, called 3B-ReLU-NMD, which parameterizes $\Theta=WH$, where $W$ has $r$ columns and $H$ has $r$ rows, allowing one to get rid of the rank constraint in Latent-ReLU-NMD. Our second contribution is to prove the convergence of a block coordinate descent (BCD) applied to 3B-ReLU-NMD and referred to as BCD-NMD. Our third contribution is a novel extrapolated variant of BCD-NMD, dubbed eBCD-NMD, which we prove is also convergent under mild assumptions. We illustrate the significant acceleration effect of eBCD-NMD compared to BCD-NMD, and also show that eBCD-NMD performs well against the state of the art on synthetic and real-world data sets.

Accelerated Algorithms for Nonlinear Matrix Decomposition with the ReLU function

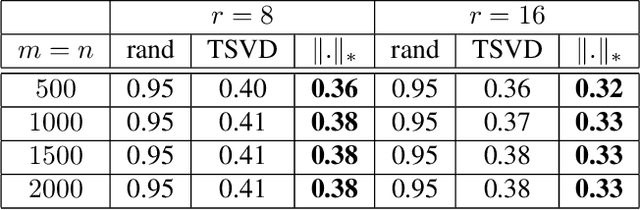
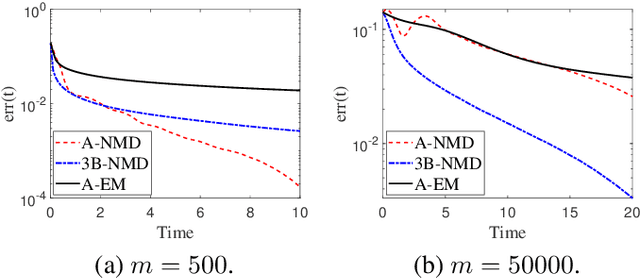
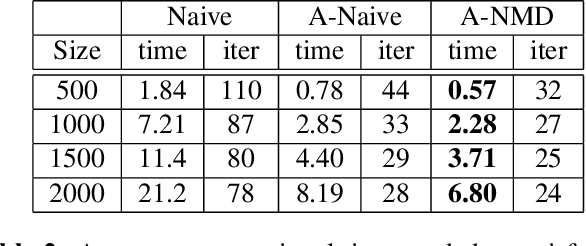
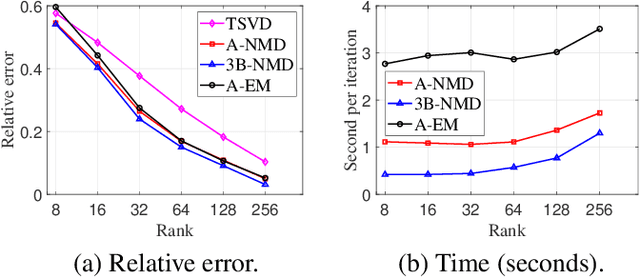
In this paper, we study the following nonlinear matrix decomposition (NMD) problem: given a sparse nonnegative matrix $X$, find a low-rank matrix $\Theta$ such that $X \approx f(\Theta)$, where $f$ is an element-wise nonlinear function. We focus on the case where $f(\cdot) = \max(0, \cdot)$, the rectified unit (ReLU) non-linear activation. We refer to the corresponding problem as ReLU-NMD. We first provide a brief overview of the existing approaches that were developed to tackle ReLU-NMD. Then we introduce two new algorithms: (1) aggressive accelerated NMD (A-NMD) which uses an adaptive Nesterov extrapolation to accelerate an existing algorithm, and (2) three-block NMD (3B-NMD) which parametrizes $\Theta = WH$ and leads to a significant reduction in the computational cost. We also propose an effective initialization strategy based on the nuclear norm as a proxy for the rank function. We illustrate the effectiveness of the proposed algorithms (available on gitlab) on synthetic and real-world data sets.