One-Shot Federated Learning with Bayesian Pseudocoresets
Paper and Code
Jun 04, 2024
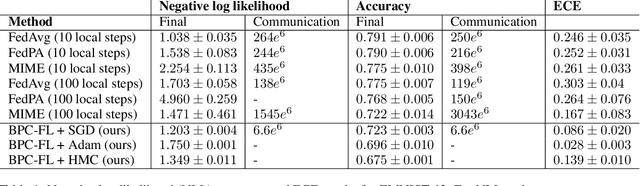
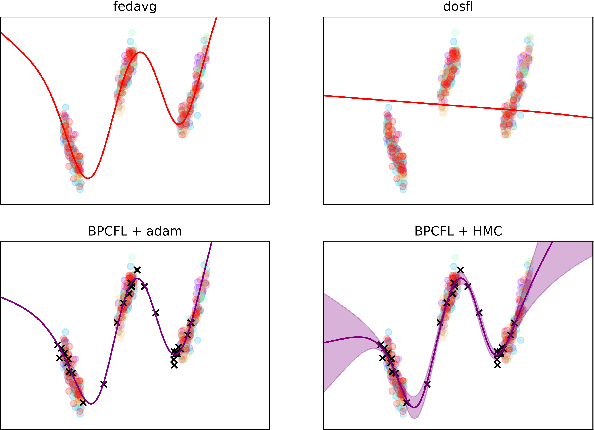

Optimization-based techniques for federated learning (FL) often come with prohibitive communication cost, as high dimensional model parameters need to be communicated repeatedly between server and clients. In this paper, we follow a Bayesian approach allowing to perform FL with one-shot communication, by solving the global inference problem as a product of local client posteriors. For models with multi-modal likelihoods, such as neural networks, a naive application of this scheme is hampered, since clients will capture different posterior modes, causing a destructive collapse of the posterior on the server side. Consequently, we explore approximate inference in the function-space representation of client posteriors, hence suffering less or not at all from multi-modality. We show that distributed function-space inference is tightly related to learning Bayesian pseudocoresets and develop a tractable Bayesian FL algorithm on this insight. We show that this approach achieves prediction performance competitive to state-of-the-art while showing a striking reduction in communication cost of up to two orders of magnitude. Moreover, due to its Bayesian nature, our method also delivers well-calibrated uncertainty estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge