Transformers as Unrolled Inference in Probabilistic Laplacian Eigenmaps: An Interpretation and Potential Improvements

We propose a probabilistic interpretation of transformers as unrolled inference steps assuming a probabilistic Laplacian Eigenmaps model from the ProbDR framework. Our derivation shows that at initialisation, transformers perform "linear" dimensionality reduction. We also show that within the transformer block, a graph Laplacian term arises from our arguments, rather than an attention matrix (which we interpret as an adjacency matrix). We demonstrate that simply subtracting the identity from the attention matrix (and thereby taking a graph diffusion step) improves validation performance on a language model and a simple vision transformer.

Towards scientific discovery with dictionary learning: Extracting biological concepts from microscopy foundation models

Dictionary learning (DL) has emerged as a powerful interpretability tool for large language models. By extracting known concepts (e.g., Golden-Gate Bridge) from human-interpretable data (e.g., text), sparse DL can elucidate a model's inner workings. In this work, we ask if DL can also be used to discover unknown concepts from less human-interpretable scientific data (e.g., cell images), ultimately enabling modern approaches to scientific discovery. As a first step, we use DL algorithms to study microscopy foundation models trained on multi-cell image data, where little prior knowledge exists regarding which high-level concepts should arise. We show that sparse dictionaries indeed extract biologically-meaningful concepts such as cell type and genetic perturbation type. We also propose a new DL algorithm, Iterative Codebook Feature Learning~(ICFL), and combine it with a pre-processing step that uses PCA whitening from a control dataset. In our experiments, we demonstrate that both ICFL and PCA improve the selectivity of extracted features compared to TopK sparse autoencoders.

The GeometricKernels Package: Heat and Matérn Kernels for Geometric Learning on Manifolds, Meshes, and Graphs

Kernels are a fundamental technical primitive in machine learning. In recent years, kernel-based methods such as Gaussian processes are becoming increasingly important in applications where quantifying uncertainty is of key interest. In settings that involve structured data defined on graphs, meshes, manifolds, or other related spaces, defining kernels with good uncertainty-quantification behavior, and computing their value numerically, is less straightforward than in the Euclidean setting. To address this difficulty, we present GeometricKernels, a software package which implements the geometric analogs of classical Euclidean squared exponential - also known as heat - and Mat\'ern kernels, which are widely-used in settings where uncertainty is of key interest. As a byproduct, we obtain the ability to compute Fourier-feature-type expansions, which are widely used in their own right, on a wide set of geometric spaces. Our implementation supports automatic differentiation in every major current framework simultaneously via a backend-agnostic design. In this companion paper to the package and its documentation, we outline the capabilities of the package and present an illustrated example of its interface. We also include a brief overview of the theory the package is built upon and provide some historic context in the appendix.

On Feature Learning for Titi Monkey Activity Detection

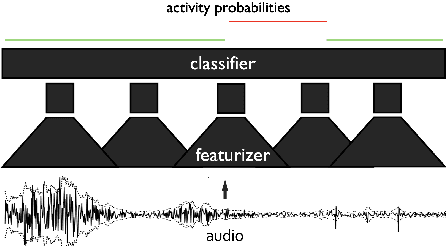
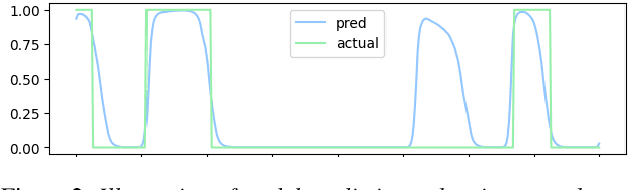
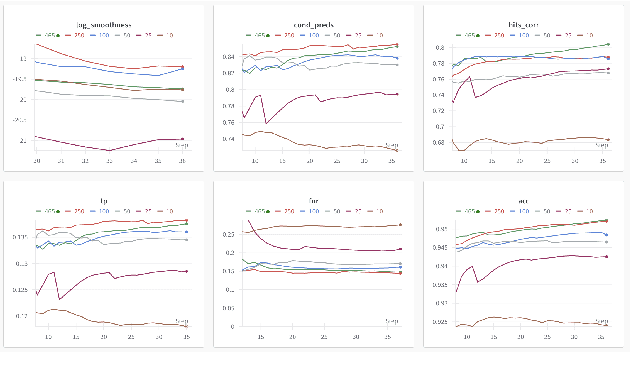
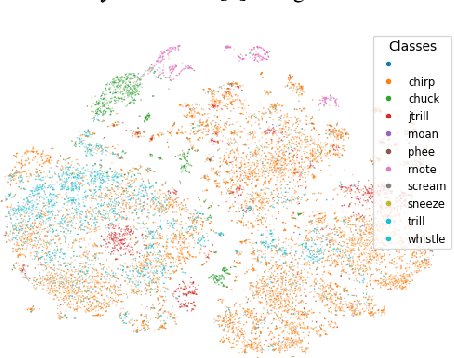
This paper, a technical summary of our preceding publication, introduces a robust machine learning framework for the detection of vocal activities of Coppery titi monkeys. Utilizing a combination of MFCC features and a bidirectional LSTM-based classifier, we effectively address the challenges posed by the small amount of expert-annotated vocal data available. Our approach significantly reduces false positives and improves the accuracy of call detection in bioacoustic research. Initial results demonstrate an accuracy of 95\% on instance predictions, highlighting the effectiveness of our model in identifying and classifying complex vocal patterns in environmental audio recordings. Moreover, we show how call classification can be done downstream, paving the way for real-world monitoring.

Towards One Model for Classical Dimensionality Reduction: A Probabilistic Perspective on UMAP and t-SNE

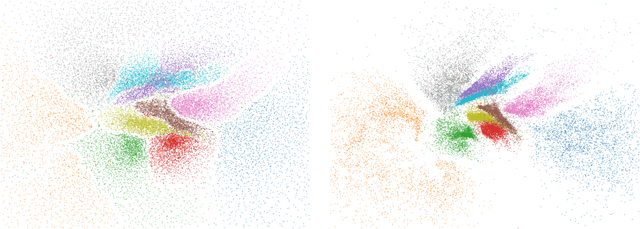
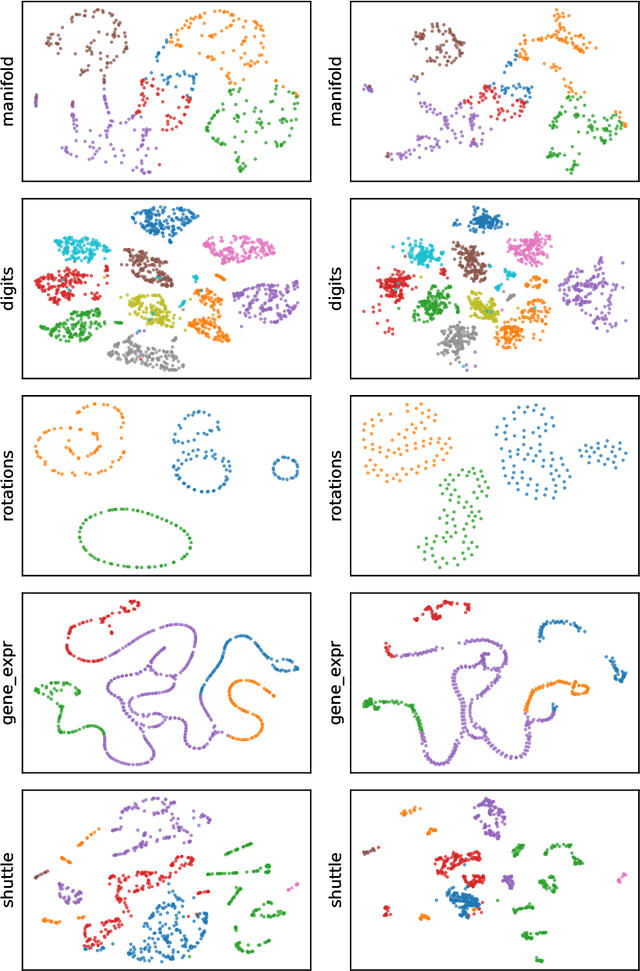
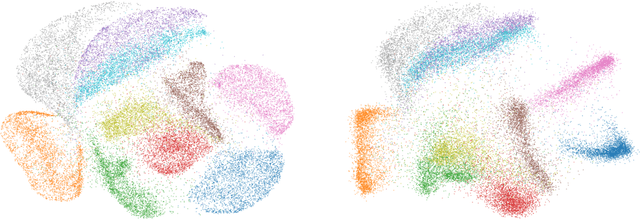
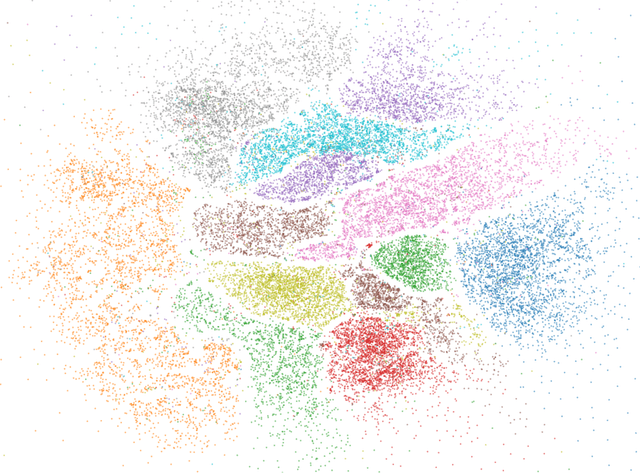
This paper shows that the dimensionality reduction methods, UMAP and t-SNE, can be approximately recast as MAP inference methods corresponding to a generalized Wishart-based model introduced in ProbDR. This interpretation offers deeper theoretical insights into these algorithms, while introducing tools with which similar dimensionality reduction methods can be studied.

Scalable Amortized GPLVMs for Single Cell Transcriptomics Data

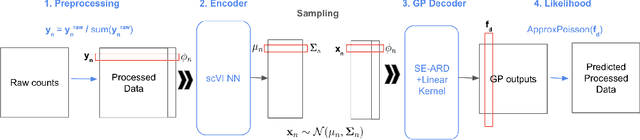
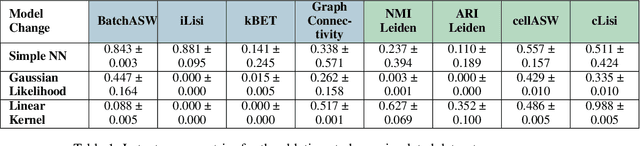
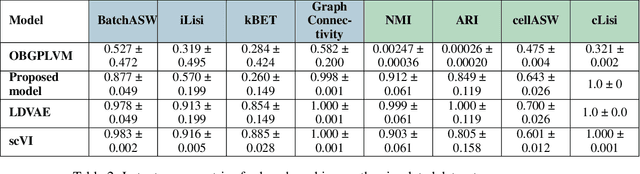
Dimensionality reduction is crucial for analyzing large-scale single-cell RNA-seq data. Gaussian Process Latent Variable Models (GPLVMs) offer an interpretable dimensionality reduction method, but current scalable models lack effectiveness in clustering cell types. We introduce an improved model, the amortized stochastic variational Bayesian GPLVM (BGPLVM), tailored for single-cell RNA-seq with specialized encoder, kernel, and likelihood designs. This model matches the performance of the leading single-cell variational inference (scVI) approach on synthetic and real-world COVID datasets and effectively incorporates cell-cycle and batch information to reveal more interpretable latent structures as we demonstrate on an innate immunity dataset.

Uncertainty as a Predictor: Leveraging Self-Supervised Learning for Zero-Shot MOS Prediction

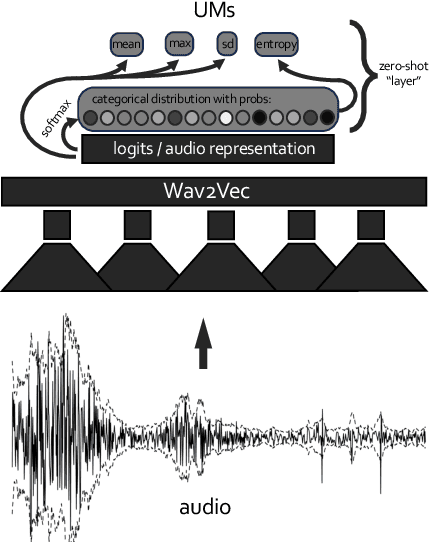
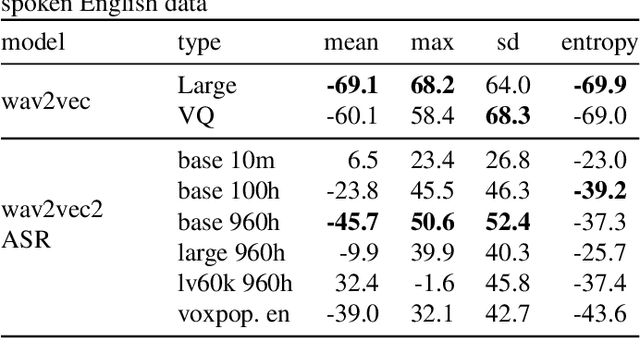
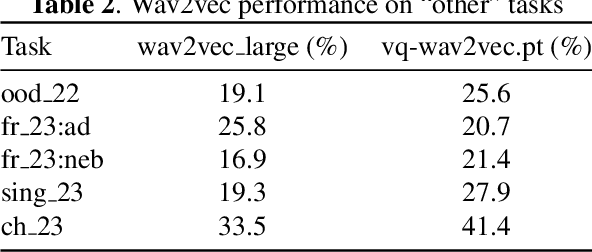
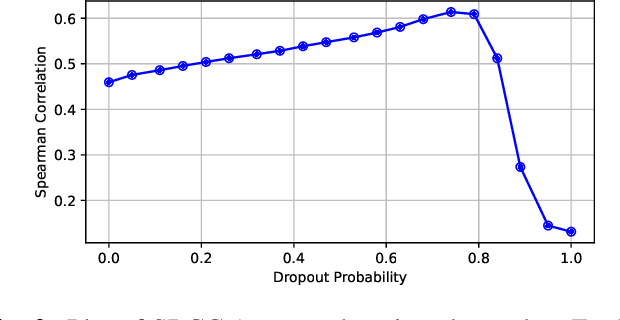
Predicting audio quality in voice synthesis and conversion systems is a critical yet challenging task, especially when traditional methods like Mean Opinion Scores (MOS) are cumbersome to collect at scale. This paper addresses the gap in efficient audio quality prediction, especially in low-resource settings where extensive MOS data from large-scale listening tests may be unavailable. We demonstrate that uncertainty measures derived from out-of-the-box pretrained self-supervised learning (SSL) models, such as wav2vec, correlate with MOS scores. These findings are based on data from the 2022 and 2023 VoiceMOS challenges. We explore the extent of this correlation across different models and language contexts, revealing insights into how inherent uncertainties in SSL models can serve as effective proxies for audio quality assessment. In particular, we show that the contrastive wav2vec models are the most performant in all settings.

Dimensionality Reduction as Probabilistic Inference

Dimensionality reduction (DR) algorithms compress high-dimensional data into a lower dimensional representation while preserving important features of the data. DR is a critical step in many analysis pipelines as it enables visualisation, noise reduction and efficient downstream processing of the data. In this work, we introduce the ProbDR variational framework, which interprets a wide range of classical DR algorithms as probabilistic inference algorithms in this framework. ProbDR encompasses PCA, CMDS, LLE, LE, MVU, diffusion maps, kPCA, Isomap, (t-)SNE, and UMAP. In our framework, a low-dimensional latent variable is used to construct a covariance, precision, or a graph Laplacian matrix, which can be used as part of a generative model for the data. Inference is done by optimizing an evidence lower bound. We demonstrate the internal consistency of our framework and show that it enables the use of probabilistic programming languages (PPLs) for DR. Additionally, we illustrate that the framework facilitates reasoning about unseen data and argue that our generative models approximate Gaussian processes (GPs) on manifolds. By providing a unified view of DR, our framework facilitates communication, reasoning about uncertainties, model composition, and extensions, particularly when domain knowledge is present.

GAUCHE: A Library for Gaussian Processes in Chemistry

We introduce GAUCHE, a library for GAUssian processes in CHEmistry. Gaussian processes have long been a cornerstone of probabilistic machine learning, affording particular advantages for uncertainty quantification and Bayesian optimisation. Extending Gaussian processes to chemical representations, however, is nontrivial, necessitating kernels defined over structured inputs such as graphs, strings and bit vectors. By defining such kernels in GAUCHE, we seek to open the door to powerful tools for uncertainty quantification and Bayesian optimisation in chemistry. Motivated by scenarios frequently encountered in experimental chemistry, we showcase applications for GAUCHE in molecular discovery and chemical reaction optimisation. The codebase is made available at https://github.com/leojklarner/gauche

Ice Core Dating using Probabilistic Programming

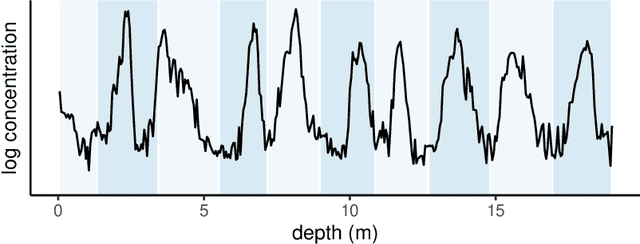
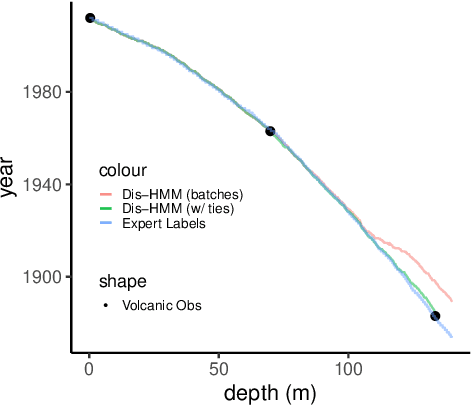
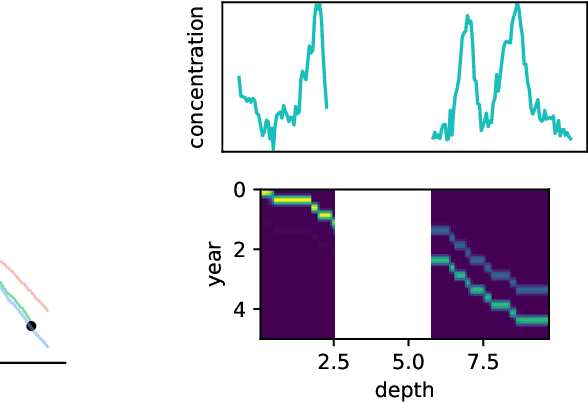
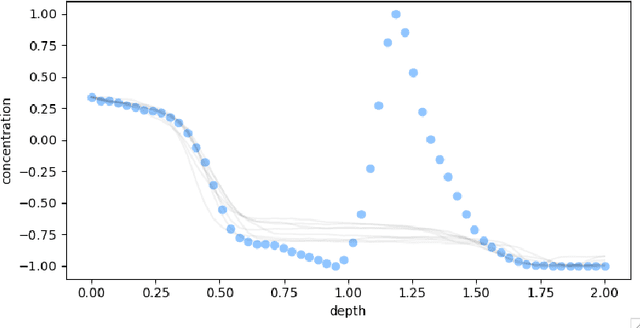
Ice cores record crucial information about past climate. However, before ice core data can have scientific value, the chronology must be inferred by estimating the age as a function of depth. Under certain conditions, chemicals locked in the ice display quasi-periodic cycles that delineate annual layers. Manually counting these noisy seasonal patterns to infer the chronology can be an imperfect and time-consuming process, and does not capture uncertainty in a principled fashion. In addition, several ice cores may be collected from a region, introducing an aspect of spatial correlation between them. We present an exploration of the use of probabilistic models for automatic dating of ice cores, using probabilistic programming to showcase its use for prototyping, automatic inference and maintainability, and demonstrate common failure modes of these tools.