Proving the NP-completeness of optimal moral graph triangulation

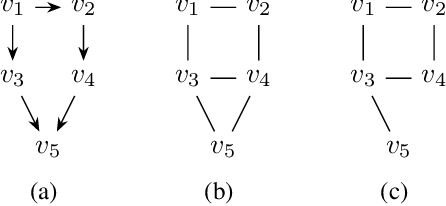
Moral graphs were introduced in the 1980s as an intermediate step when transforming a Bayesian network to a junction tree, on which exact belief propagation can be efficiently done. The moral graph of a Bayesian network can be trivially obtained by connecting non-adjacent parents for each node in the Bayesian network and dropping the direction of each edge. Perhaps because the moralization process looks simple, there has been little attention on the properties of moral graphs and their impact in belief propagation on Bayesian networks. This paper addresses the mistaken claim that it has been previously proved that optimal moral graph triangulation with the constraints of minimum fill-in, treewidth or total states is NP-complete. The problems are in fact NP-complete, but they have not previously been proved. We now prove these.