Kevin Korb
Proving the NP-completeness of optimal moral graph triangulation
Mar 06, 2019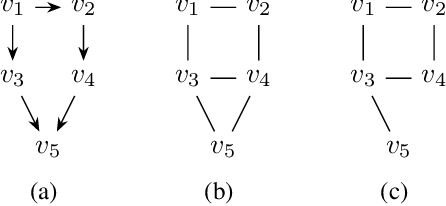
Abstract:Moral graphs were introduced in the 1980s as an intermediate step when transforming a Bayesian network to a junction tree, on which exact belief propagation can be efficiently done. The moral graph of a Bayesian network can be trivially obtained by connecting non-adjacent parents for each node in the Bayesian network and dropping the direction of each edge. Perhaps because the moralization process looks simple, there has been little attention on the properties of moral graphs and their impact in belief propagation on Bayesian networks. This paper addresses the mistaken claim that it has been previously proved that optimal moral graph triangulation with the constraints of minimum fill-in, treewidth or total states is NP-complete. The problems are in fact NP-complete, but they have not previously been proved. We now prove these.
The Complexity of Morality: Checking Markov Blanket Consistency with DAGs via Morality
Mar 05, 2019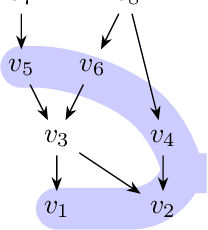
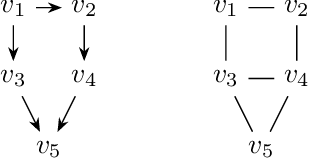
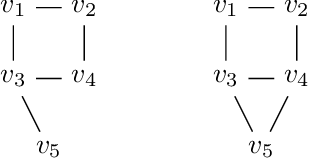
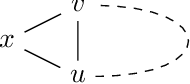
Abstract:A family of Markov blankets in a faithful Bayesian network satisfies the symmetry and consistency properties. In this paper, we draw a bijection between families of consistent Markov blankets and moral graphs. We define the new concepts of weak recursive simpliciality and perfect elimination kits. We prove that they are equivalent to graph morality. In addition, we prove that morality can be decided in polynomial time for graphs with maximum degree less than $5$, but the problem is NP-complete for graphs with higher maximum degrees.
Digital Genesis: Computers, Evolution and Artificial Life
Dec 07, 2015Abstract:The application of evolution in the digital realm, with the goal of creating artificial intelligence and artificial life, has a history as long as that of the digital computer itself. We illustrate the intertwined history of these ideas, starting with the early theoretical work of John von Neumann and the pioneering experimental work of Nils Aall Barricelli. We argue that evolutionary thinking and artificial life will continue to play an integral role in the future development of the digital world.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge