Redundant Sudoku Rules
Paper and Code
Jul 25, 2012
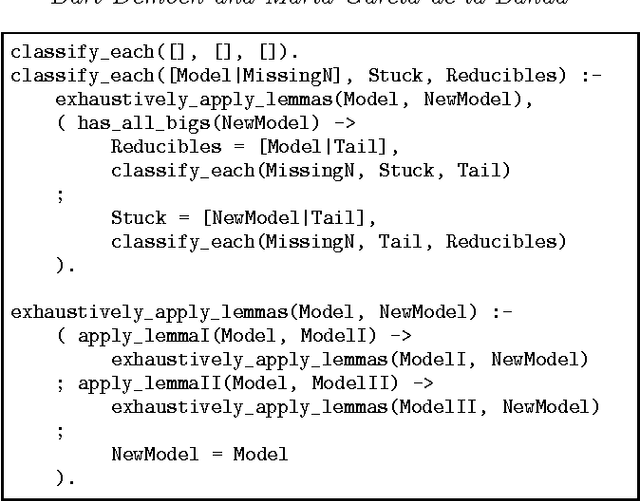

The rules of Sudoku are often specified using twenty seven \texttt{all\_different} constraints, referred to as the {\em big} \mrules. Using graphical proofs and exploratory logic programming, the following main and new result is obtained: many subsets of six of these big \mrules are redundant (i.e., they are entailed by the remaining twenty one \mrules), and six is maximal (i.e., removing more than six \mrules is not possible while maintaining equivalence). The corresponding result for binary inequality constraints, referred to as the {\em small} \mrules, is stated as a conjecture.
* 14 pages, 161 figures, to appear in TPLP
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge