Bag-of-Word-Groups (BoWG): A Robust and Efficient Loop Closure Detection Method Under Perceptual Aliasing

Loop closure is critical in Simultaneous Localization and Mapping (SLAM) systems to reduce accumulative drift and ensure global mapping consistency. However, conventional methods struggle in perceptually aliased environments, such as narrow pipes, due to vector quantization, feature sparsity, and repetitive textures, while existing solutions often incur high computational costs. This paper presents Bag-of-Word-Groups (BoWG), a novel loop closure detection method that achieves superior precision-recall, robustness, and computational efficiency. The core innovation lies in the introduction of word groups, which captures the spatial co-occurrence and proximity of visual words to construct an online dictionary. Additionally, drawing inspiration from probabilistic transition models, we incorporate temporal consistency directly into similarity computation with an adaptive scheme, substantially improving precision-recall performance. The method is further strengthened by a feature distribution analysis module and dedicated post-verification mechanisms. To evaluate the effectiveness of our method, we conduct experiments on both public datasets and a confined-pipe dataset we constructed. Results demonstrate that BoWG surpasses state-of-the-art methods, including both traditional and learning-based approaches, in terms of precision-recall and computational efficiency. Our approach also exhibits excellent scalability, achieving an average processing time of 16 ms per image across 17,565 images in the Bicocca25b dataset.

Multi-CAP: A Multi-Robot Connectivity-Aware Hierarchical Coverage Path Planning Algorithm for Unknown Environments

Efficient coordination of multiple robots for coverage of large, unknown environments is a significant challenge that involves minimizing the total coverage path length while reducing inter-robot conflicts. In this paper, we introduce a Multi-robot Connectivity-Aware Planner (Multi-CAP), a hierarchical coverage path planning algorithm that facilitates multi-robot coordination through a novel connectivity-aware approach. The algorithm constructs and dynamically maintains an adjacency graph that represents the environment as a set of connected subareas. Critically, we make the assumption that the environment, while unknown, is bounded. This allows for incremental refinement of the adjacency graph online to ensure its structure represents the physical layout of the space, both in observed and unobserved areas of the map as robots explore the environment. We frame the task of assigning subareas to robots as a Vehicle Routing Problem (VRP), a well-studied problem for finding optimal routes for a fleet of vehicles. This is used to compute disjoint tours that minimize redundant travel, assigning each robot a unique, non-conflicting set of subareas. Each robot then executes its assigned tour, independently adapting its coverage strategy within each subarea to minimize path length based on real-time sensor observations of the subarea. We demonstrate through simulations and multi-robot hardware experiments that Multi-CAP significantly outperforms state-of-the-art methods in key metrics, including coverage time, total path length, and path overlap ratio. Ablation studies further validate the critical role of our connectivity-aware graph and the global tour planner in achieving these performance gains.

NavMoE: Hybrid Model- and Learning-based Traversability Estimation for Local Navigation via Mixture of Experts

This paper explores traversability estimation for robot navigation. A key bottleneck in traversability estimation lies in efficiently achieving reliable and robust predictions while accurately encoding both geometric and semantic information across diverse environments. We introduce Navigation via Mixture of Experts (NAVMOE), a hierarchical and modular approach for traversability estimation and local navigation. NAVMOE combines multiple specialized models for specific terrain types, each of which can be either a classical model-based or a learning-based approach that predicts traversability for specific terrain types. NAVMOE dynamically weights the contributions of different models based on the input environment through a gating network. Overall, our approach offers three advantages: First, NAVMOE enables traversability estimation to adaptively leverage specialized approaches for different terrains, which enhances generalization across diverse and unseen environments. Second, our approach significantly improves efficiency with negligible cost of solution quality by introducing a training-free lazy gating mechanism, which is designed to minimize the number of activated experts during inference. Third, our approach uses a two-stage training strategy that enables the training for the gating networks within the hybrid MoE method that contains nondifferentiable modules. Extensive experiments show that NAVMOE delivers a better efficiency and performance balance than any individual expert or full ensemble across different domains, improving cross- domain generalization and reducing average computational cost by 81.2% via lazy gating, with less than a 2% loss in path quality.

Parallel, Asymptotically Optimal Algorithms for Moving Target Traveling Salesman Problems

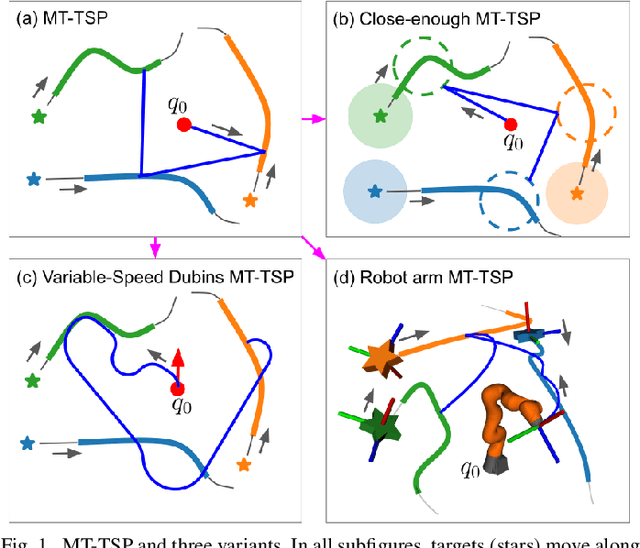
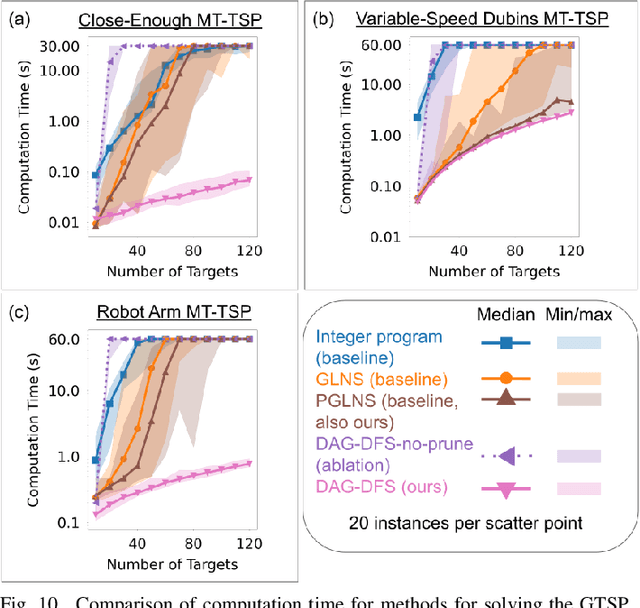
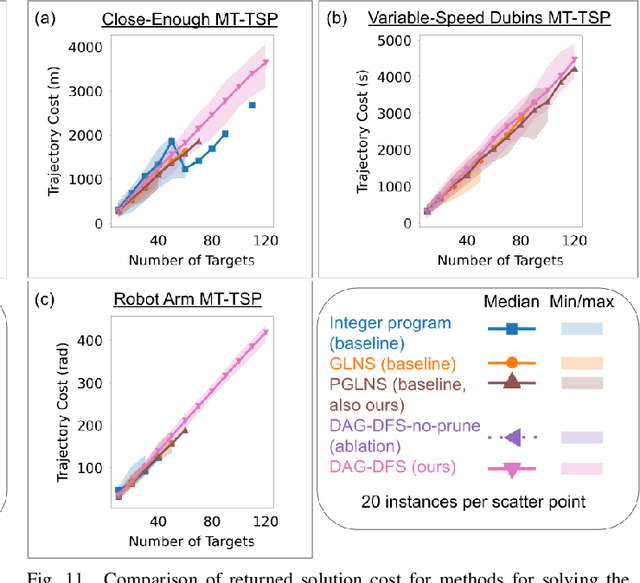
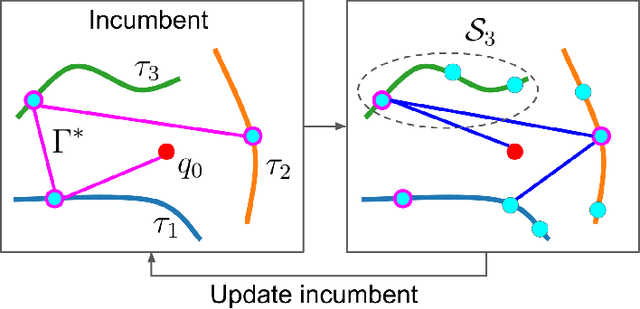
The Moving Target Traveling Salesman Problem (MT-TSP) seeks an agent trajectory that intercepts several moving targets, within a particular time window for each target. In the presence of generic nonlinear target trajectories or kinematic constraints on the agent, no prior algorithm guarantees convergence to an optimal MT-TSP solution. Therefore, we introduce the Iterated Random Generalized (IRG) TSP framework. The key idea behind IRG is to alternate between randomly sampling a set of agent configuration-time points, corresponding to interceptions of targets, and finding a sequence of interception points by solving a generalized TSP (GTSP). This alternation enables asymptotic convergence to the optimum. We introduce two parallel algorithms within the IRG framework. The first algorithm, IRG-PGLNS, solves GTSPs using PGLNS, our parallelized extension of the state-of-the-art solver GLNS. The second algorithm, Parallel Communicating GTSPs (PCG), solves GTSPs corresponding to several sets of points simultaneously. We present numerical results for three variants of the MT-TSP: one where intercepting a target only requires coming within a particular distance, another where the agent is a variable-speed Dubins car, and a third where the agent is a redundant robot arm. We show that IRG-PGLNS and PCG both converge faster than a baseline based on prior work.

A-MHA*: Anytime Multi-Heuristic A*

Designing good heuristic functions for graph search requires adequate domain knowledge. It is often easy to design heuristics that perform well and correlate with the underlying true cost-to-go values in certain parts of the search space but these may not be admissible throughout the domain thereby affecting the optimality guarantees of the search. Bounded suboptimal search using several such partially good but inadmissible heuristics was developed in Multi-Heuristic A* (MHA*). Although MHA* leverages multiple inadmissible heuristics to potentially generate a faster suboptimal solution, the original version does not improve the solution over time. It is a one shot algorithm that requires careful setting of inflation factors to obtain a desired one time solution. In this work, we tackle this issue by extending MHA* to an anytime version that finds a feasible suboptimal solution quickly and continually improves it until time runs out. Our work is inspired from the Anytime Repairing A* (ARA*) algorithm. We prove that our precise adaptation of ARA* concepts in the MHA* framework preserves the original suboptimal and completeness guarantees and enhances MHA* to perform in an anytime fashion. Furthermore, we report the performance of A-MHA* in 3-D path planning domain and sliding tiles puzzle and compare against MHA* and other anytime algorithms.

Optimizing Start Locations in Ergodic Search for Disaster Response

In disaster response scenarios, deploying robotic teams effectively is crucial for improving situational awareness and enhancing search and rescue operations. The use of robots in search and rescue has been studied but the question of where to start robot deployments has not been addressed. This work addresses the problem of optimally selecting starting locations for robots with heterogeneous capabilities by formulating a joint optimization problem. To determine start locations, this work adds a constraint to the ergodic optimization framework whose minimum assigns robots to start locations. This becomes a little more challenging when the robots are heterogeneous (equipped with different sensing and motion modalities) because not all robots start at the same location, and a more complex adaptation of the aforementioned constraint is applied. Our method assumes access to potential starting locations, which can be obtained from expert knowledge or aerial imagery. We experimentally evaluate the efficacy of our joint optimization approach by comparing it to baseline methods that use fixed starting locations for all robots. Our experimental results show significant gains in coverage performance, with average improvements of 35.98% on synthetic data and 31.91% on real-world data for homogeneous and heterogeneous teams, in terms of the ergodic metric.

Automatic Cannulation of Femoral Vessels in a Porcine Shock Model

Rapid and reliable vascular access is critical in trauma and critical care. Central vascular catheterization enables high-volume resuscitation, hemodynamic monitoring, and advanced interventions like ECMO and REBOA. While peripheral access is common, central access is often necessary but requires specialized ultrasound-guided skills, posing challenges in prehospital settings. The complexity arises from deep target vessels and the precision needed for needle placement. Traditional techniques, like the Seldinger method, demand expertise to avoid complications. Despite its importance, ultrasound-guided central access is underutilized due to limited field expertise. While autonomous needle insertion has been explored for peripheral vessels, only semi-autonomous methods exist for femoral access. This work advances toward full automation, integrating robotic ultrasound for minimally invasive emergency procedures. Our key contribution is the successful femoral vein and artery cannulation in a porcine hemorrhagic shock model.

A Complete and Bounded-Suboptimal Algorithm for a Moving Target Traveling Salesman Problem with Obstacles in 3D

The moving target traveling salesman problem with obstacles (MT-TSP-O) seeks an obstacle-free trajectory for an agent that intercepts a given set of moving targets, each within specified time windows, and returns to the agent's starting position. Each target moves with a constant velocity within its time windows, and the agent has a speed limit no smaller than any target's speed. We present FMC*-TSP, the first complete and bounded-suboptimal algorithm for the MT-TSP-O, and results for an agent whose configuration space is $\mathbb{R}^3$. Our algorithm interleaves a high-level search and a low-level search, where the high-level search solves a generalized traveling salesman problem with time windows (GTSP-TW) to find a sequence of targets and corresponding time windows for the agent to visit. Given such a sequence, the low-level search then finds an associated agent trajectory. To solve the low-level planning problem, we develop a new algorithm called FMC*, which finds a shortest path on a graph of convex sets (GCS) via implicit graph search and pruning techniques specialized for problems with moving targets. We test FMC*-TSP on 280 problem instances with up to 40 targets and demonstrate its smaller median runtime than a baseline based on prior work.

Multi-Agent Ergodic Exploration under Smoke-Based, Time-Varying Sensor Visibility Constraints

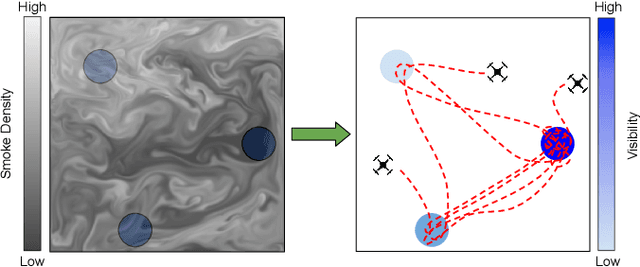
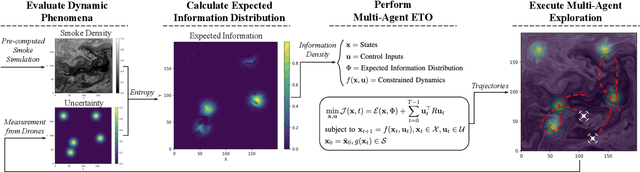
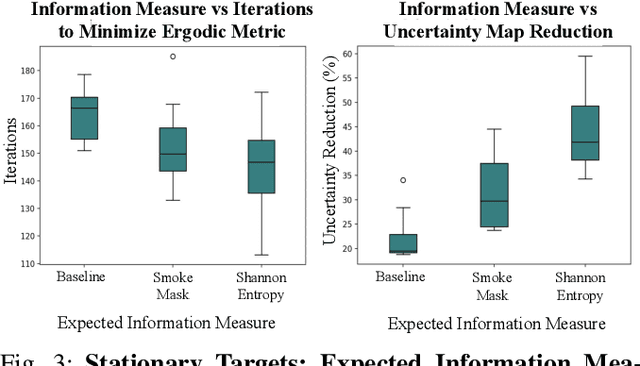
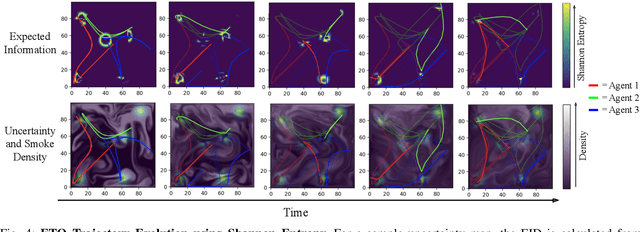
In this work, we consider the problem of multi-agent informative path planning (IPP) for robots whose sensor visibility continuously changes as a consequence of a time-varying natural phenomenon. We leverage ergodic trajectory optimization (ETO), which generates paths such that the amount of time an agent spends in an area is proportional to the expected information in that area. We focus specifically on the problem of multi-agent drone search of a wildfire, where we use the time-varying environmental process of smoke diffusion to construct a sensor visibility model. This sensor visibility model is used to repeatedly calculate an expected information distribution (EID) to be used in the ETO algorithm. Our experiments show that our exploration method achieves improved information gathering over both baseline search methods and naive ergodic search formulations.

Ergodic Exploration over Meshable Surfaces

Robotic search and rescue, exploration, and inspection require trajectory planning across a variety of domains. A popular approach to trajectory planning for these types of missions is ergodic search, which biases a trajectory to spend time in parts of the exploration domain that are believed to contain more information. Most prior work on ergodic search has been limited to searching simple surfaces, like a 2D Euclidean plane or a sphere, as they rely on projecting functions defined on the exploration domain onto analytically obtained Fourier basis functions. In this paper, we extend ergodic search to any surface that can be approximated by a triangle mesh. The basis functions are approximated through finite element methods on a triangle mesh of the domain. We formally prove that this approximation converges to the continuous case as the mesh approximation converges to the true domain. We demonstrate that on domains where analytical basis functions are available (plane, sphere), the proposed method obtains equivalent results, and while on other domains (torus, bunny, wind turbine), the approach is versatile enough to still search effectively. Lastly, we also compare with an existing ergodic search technique that can handle complex domains and show that our method results in a higher quality exploration.