Bhaskar Vundurthy
Multi-CAP: A Multi-Robot Connectivity-Aware Hierarchical Coverage Path Planning Algorithm for Unknown Environments
Sep 18, 2025Abstract:Efficient coordination of multiple robots for coverage of large, unknown environments is a significant challenge that involves minimizing the total coverage path length while reducing inter-robot conflicts. In this paper, we introduce a Multi-robot Connectivity-Aware Planner (Multi-CAP), a hierarchical coverage path planning algorithm that facilitates multi-robot coordination through a novel connectivity-aware approach. The algorithm constructs and dynamically maintains an adjacency graph that represents the environment as a set of connected subareas. Critically, we make the assumption that the environment, while unknown, is bounded. This allows for incremental refinement of the adjacency graph online to ensure its structure represents the physical layout of the space, both in observed and unobserved areas of the map as robots explore the environment. We frame the task of assigning subareas to robots as a Vehicle Routing Problem (VRP), a well-studied problem for finding optimal routes for a fleet of vehicles. This is used to compute disjoint tours that minimize redundant travel, assigning each robot a unique, non-conflicting set of subareas. Each robot then executes its assigned tour, independently adapting its coverage strategy within each subarea to minimize path length based on real-time sensor observations of the subarea. We demonstrate through simulations and multi-robot hardware experiments that Multi-CAP significantly outperforms state-of-the-art methods in key metrics, including coverage time, total path length, and path overlap ratio. Ablation studies further validate the critical role of our connectivity-aware graph and the global tour planner in achieving these performance gains.
Parallel, Asymptotically Optimal Algorithms for Moving Target Traveling Salesman Problems
Sep 10, 2025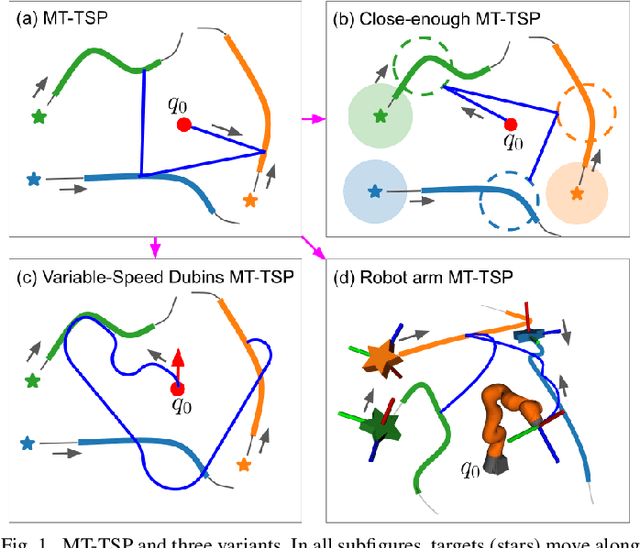
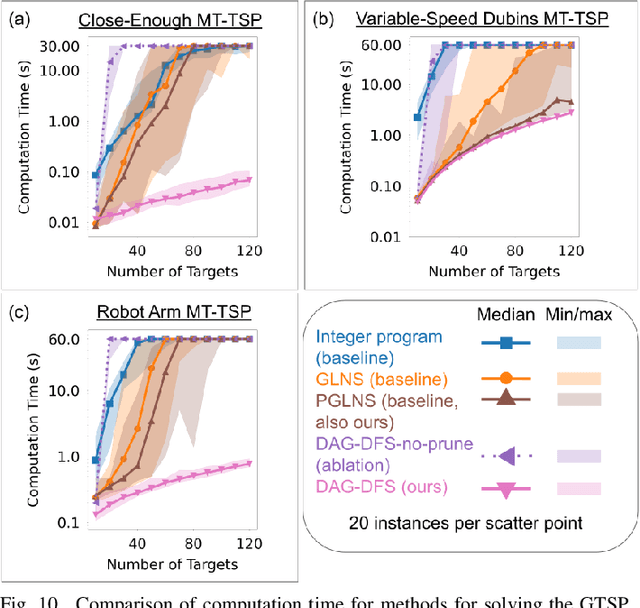
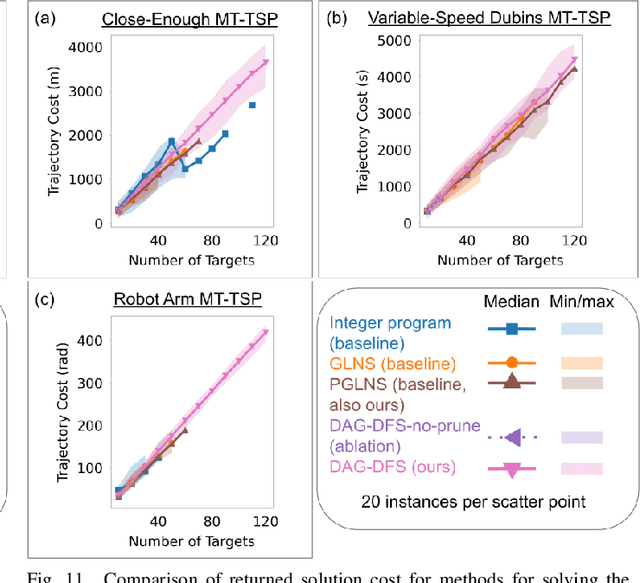
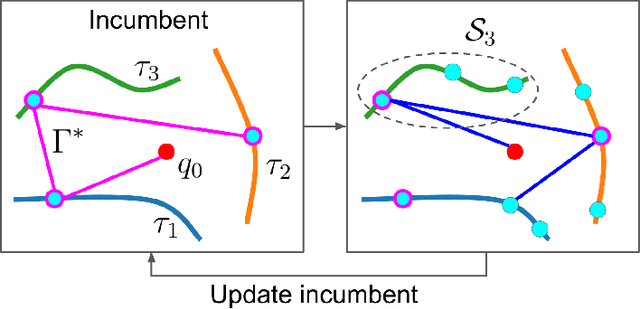
Abstract:The Moving Target Traveling Salesman Problem (MT-TSP) seeks an agent trajectory that intercepts several moving targets, within a particular time window for each target. In the presence of generic nonlinear target trajectories or kinematic constraints on the agent, no prior algorithm guarantees convergence to an optimal MT-TSP solution. Therefore, we introduce the Iterated Random Generalized (IRG) TSP framework. The key idea behind IRG is to alternate between randomly sampling a set of agent configuration-time points, corresponding to interceptions of targets, and finding a sequence of interception points by solving a generalized TSP (GTSP). This alternation enables asymptotic convergence to the optimum. We introduce two parallel algorithms within the IRG framework. The first algorithm, IRG-PGLNS, solves GTSPs using PGLNS, our parallelized extension of the state-of-the-art solver GLNS. The second algorithm, Parallel Communicating GTSPs (PCG), solves GTSPs corresponding to several sets of points simultaneously. We present numerical results for three variants of the MT-TSP: one where intercepting a target only requires coming within a particular distance, another where the agent is a variable-speed Dubins car, and a third where the agent is a redundant robot arm. We show that IRG-PGLNS and PCG both converge faster than a baseline based on prior work.
A Complete and Bounded-Suboptimal Algorithm for a Moving Target Traveling Salesman Problem with Obstacles in 3D
Apr 20, 2025Abstract:The moving target traveling salesman problem with obstacles (MT-TSP-O) seeks an obstacle-free trajectory for an agent that intercepts a given set of moving targets, each within specified time windows, and returns to the agent's starting position. Each target moves with a constant velocity within its time windows, and the agent has a speed limit no smaller than any target's speed. We present FMC*-TSP, the first complete and bounded-suboptimal algorithm for the MT-TSP-O, and results for an agent whose configuration space is $\mathbb{R}^3$. Our algorithm interleaves a high-level search and a low-level search, where the high-level search solves a generalized traveling salesman problem with time windows (GTSP-TW) to find a sequence of targets and corresponding time windows for the agent to visit. Given such a sequence, the low-level search then finds an associated agent trajectory. To solve the low-level planning problem, we develop a new algorithm called FMC*, which finds a shortest path on a graph of convex sets (GCS) via implicit graph search and pruning techniques specialized for problems with moving targets. We test FMC*-TSP on 280 problem instances with up to 40 targets and demonstrate its smaller median runtime than a baseline based on prior work.
A Complete Algorithm for a Moving Target Traveling Salesman Problem with Obstacles
Sep 15, 2024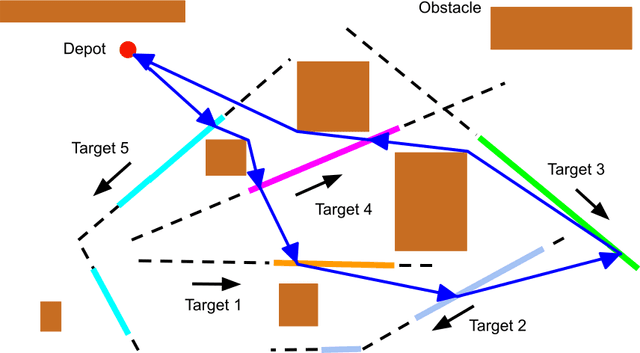

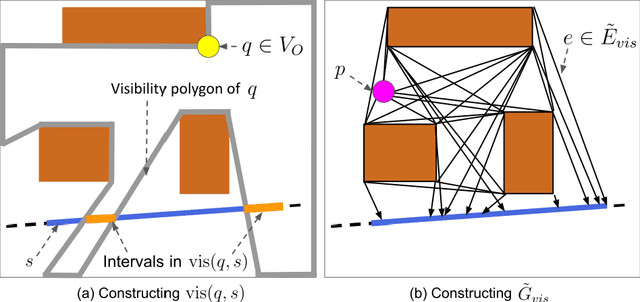
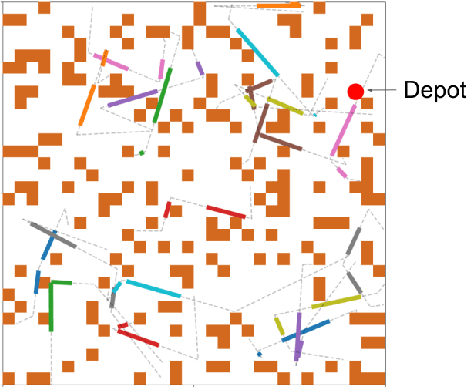
Abstract:The moving target traveling salesman problem with obstacles (MT-TSP-O) is a generalization of the traveling salesman problem (TSP) where, as its name suggests, the targets are moving. A solution to the MT-TSP-O is a trajectory that visits each moving target during a certain time window(s), and this trajectory avoids stationary obstacles. We assume each target moves at a constant velocity during each of its time windows. The agent has a speed limit, and this speed limit is no smaller than any target's speed. This paper presents the first complete algorithm for finding feasible solutions to the MT-TSP-O. Our algorithm builds a tree where the nodes are agent trajectories intercepting a unique sequence of targets within a unique sequence of time windows. We generate each of a parent node's children by extending the parent's trajectory to intercept one additional target, each child corresponding to a different choice of target and time window. This extension consists of planning a trajectory from the parent trajectory's final point in space-time to a moving target. To solve this point-to-moving-target subproblem, we define a novel generalization of a visibility graph called a moving target visibility graph (MTVG). Our overall algorithm is called MTVG-TSP. To validate MTVG-TSP, we test it on 570 instances with up to 30 targets. We implement a baseline method that samples trajectories of targets into points, based on prior work on special cases of the MT-TSP-O. MTVG-TSP finds feasible solutions in all cases where the baseline does, and when the sum of the targets' time window lengths enters a critical range, MTVG-TSP finds a feasible solution with up to 38 times less computation time.
Measure Preserving Flows for Ergodic Search in Convoluted Environments
Sep 13, 2024



Abstract:Autonomous robotic search has important applications in robotics, such as the search for signs of life after a disaster. When \emph{a priori} information is available, for example in the form of a distribution, a planner can use that distribution to guide the search. Ergodic search is one method that uses the information distribution to generate a trajectory that minimizes the ergodic metric, in that it encourages the robot to spend more time in regions with high information and proportionally less time in the remaining regions. Unfortunately, prior works in ergodic search do not perform well in complex environments with obstacles such as a building's interior or a maze. To address this, our work presents a modified ergodic metric using the Laplace-Beltrami eigenfunctions to capture map geometry and obstacle locations within the ergodic metric. Further, we introduce an approach to generate trajectories that minimize the ergodic metric while guaranteeing obstacle avoidance using measure-preserving vector fields. Finally, we leverage the divergence-free nature of these vector fields to generate collision-free trajectories for multiple agents. We demonstrate our approach via simulations with single and multi-agent systems on maps representing interior hallways and long corridors with non-uniform information distribution. In particular, we illustrate the generation of feasible trajectories in complex environments where prior methods fail.
Modular, Resilient, and Scalable System Design Approaches -- Lessons learned in the years after DARPA Subterranean Challenge
Apr 27, 2024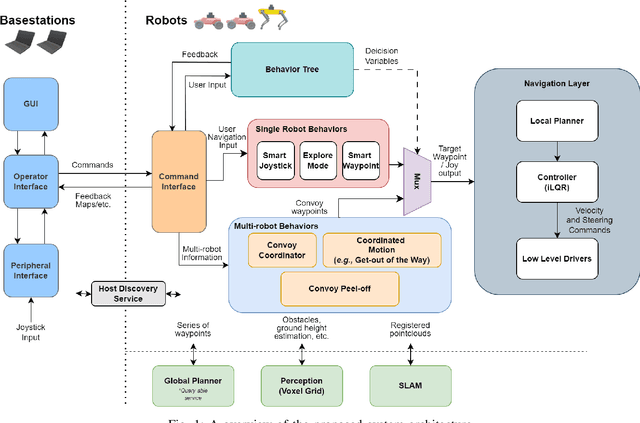
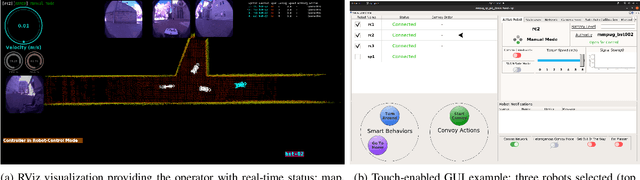
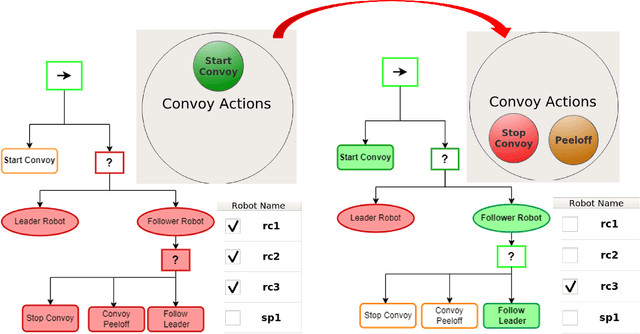
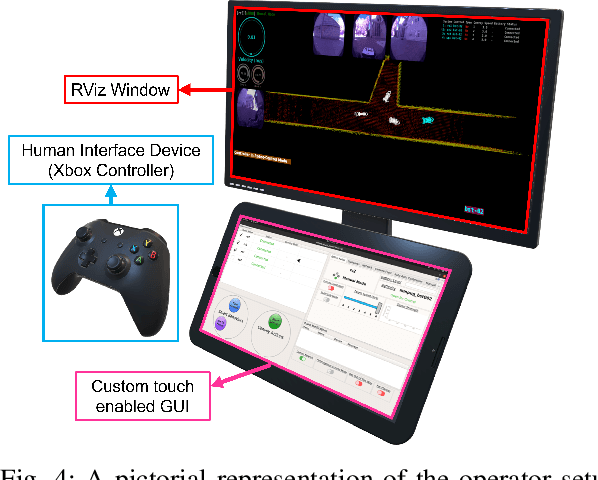
Abstract:Field robotics applications, such as search and rescue, involve robots operating in large, unknown areas. These environments present unique challenges that compound the difficulties faced by a robot operator. The use of multi-robot teams, assisted by carefully designed autonomy, help reduce operator workload and allow the operator to effectively coordinate robot capabilities. In this work, we present a system architecture designed to optimize both robot autonomy and the operator experience in multi-robot scenarios. Drawing on lessons learned from our team's participation in the DARPA SubT Challenge, our architecture emphasizes modularity and interoperability. We empower the operator by allowing for adjustable levels of autonomy ("sliding mode autonomy"). We enhance the operator experience by using intuitive, adaptive interfaces that suggest context-aware actions to simplify control. Finally, we describe how the proposed architecture enables streamlined development of new capabilities for effective deployment of robot autonomy in the field.
Multi-agent Collective Construction using 3D Decomposition
Sep 02, 2023



Abstract:This paper addresses a Multi-Agent Collective Construction (MACC) problem that aims to build a three-dimensional structure comprised of cubic blocks. We use cube-shaped robots that can carry one cubic block at a time, and move forward, reverse, left, and right to an adjacent cell of the same height or climb up and down one cube height. To construct structures taller than one cube, the robots must build supporting stairs made of blocks and remove the stairs once the structure is built. Conventional techniques solve for the entire structure at once and quickly become intractable for larger workspaces and complex structures, especially in a multi-agent setting. To this end, we present a decomposition algorithm that computes valid substructures based on intrinsic structural dependencies. We use Mixed Integer Linear Programming (MILP) to solve for each of these substructures and then aggregate the solutions to construct the entire structure. Extensive testing on 200 randomly generated structures shows an order of magnitude improvement in the solution computation time compared to an MILP approach without decomposition. Additionally, compared to Reinforcement Learning (RL) based and heuristics-based approaches drawn from the literature, our solution indicates orders of magnitude improvement in the number of pick-up and drop-off actions required to construct a structure. Furthermore, we leverage the independence between substructures to detect which sub-structures can be built in parallel. With this parallelization technique, we illustrate a further improvement in the number of time steps required to complete building the structure. This work is a step towards applying multi-agent collective construction for real-world structures by significantly reducing solution computation time with a bounded increase in the number of time steps required to build the structure.
High Speed Convoy in Unstructured Indoor Environments
Nov 11, 2022Abstract:Practical operations of coordinated fleets of mobile robots in different environments reveal benefits of maintaining small distances between robots as they move at higher speeds. This is counter-intuitive in that as speed increases, increased distances would give robots a larger time to respond to sudden motion variations in surrounding robots. However, there is a desire to have lower inter-robot distances in examples like autonomous trucks on highways to optimize energy by vehicle drafting or smaller robots in cluttered environments to maintain communication, etc. This work introduces a model based control framework that directly takes non-linear system dynamics into account. Each robot is able to follow closer at high speeds because it makes predictions on the state information from its adjacent robots and biases it's response by anticipating adjacent robots' motion. In contrast to existing controllers, our non-linear model based predictive decentralized controller is able to achieve lower inter-robot distances at higher speeds. We demonstrate the success of our approach through simulated and hardware results on mobile ground robots.
Fast Staircase Detection and Estimation using 3D Point Clouds with Multi-detection Merging for Heterogeneous Robots
Nov 01, 2022Abstract:Robotic systems need advanced mobility capabilities to operate in complex, three-dimensional environments designed for human use, e.g., multi-level buildings. Incorporating some level of autonomy enables robots to operate robustly, reliably, and efficiently in such complex environments, e.g., automatically ``returning home'' if communication between an operator and robot is lost during deployment. This work presents a novel method that enables mobile robots to robustly operate in multi-level environments by making it possible to autonomously locate and climb a range of different staircases. We present results wherein a wheeled robot works together with a quadrupedal system to quickly detect different staircases and reliably climb them. The performance of this novel staircase detection algorithm that is able to run on the heterogeneous platforms is compared to the current state-of-the-art detection algorithm. We show that our approach significantly increases the accuracy and speed at which detections occur.
Mathematical Justification of Hard Negative Mining via Isometric Approximation Theorem
Oct 20, 2022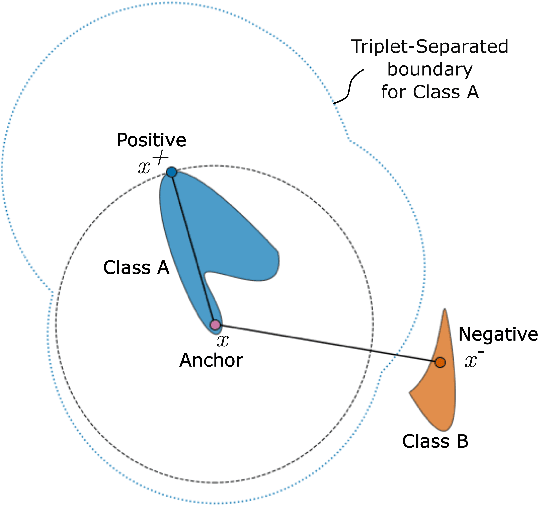
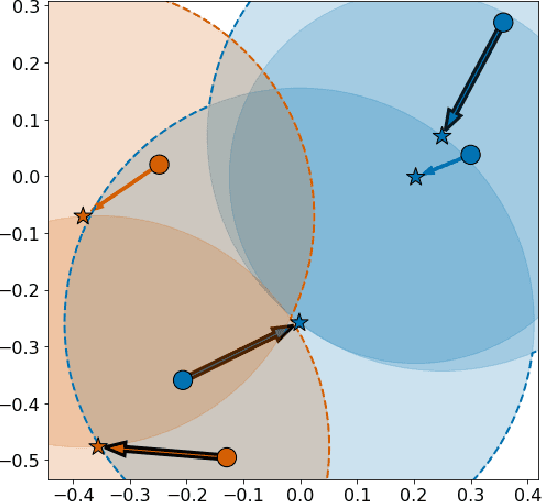
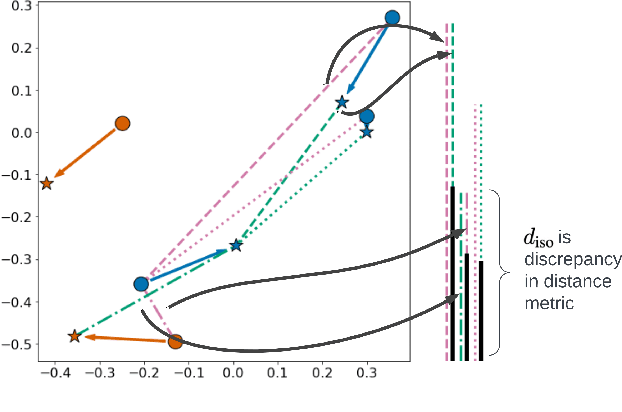
Abstract:In deep metric learning, the Triplet Loss has emerged as a popular method to learn many computer vision and natural language processing tasks such as facial recognition, object detection, and visual-semantic embeddings. One issue that plagues the Triplet Loss is network collapse, an undesirable phenomenon where the network projects the embeddings of all data onto a single point. Researchers predominately solve this problem by using triplet mining strategies. While hard negative mining is the most effective of these strategies, existing formulations lack strong theoretical justification for their empirical success. In this paper, we utilize the mathematical theory of isometric approximation to show an equivalence between the Triplet Loss sampled by hard negative mining and an optimization problem that minimizes a Hausdorff-like distance between the neural network and its ideal counterpart function. This provides the theoretical justifications for hard negative mining's empirical efficacy. In addition, our novel application of the isometric approximation theorem provides the groundwork for future forms of hard negative mining that avoid network collapse. Our theory can also be extended to analyze other Euclidean space-based metric learning methods like Ladder Loss or Contrastive Learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge