A Complete and Bounded-Suboptimal Algorithm for a Moving Target Traveling Salesman Problem with Obstacles in 3D

The moving target traveling salesman problem with obstacles (MT-TSP-O) seeks an obstacle-free trajectory for an agent that intercepts a given set of moving targets, each within specified time windows, and returns to the agent's starting position. Each target moves with a constant velocity within its time windows, and the agent has a speed limit no smaller than any target's speed. We present FMC*-TSP, the first complete and bounded-suboptimal algorithm for the MT-TSP-O, and results for an agent whose configuration space is $\mathbb{R}^3$. Our algorithm interleaves a high-level search and a low-level search, where the high-level search solves a generalized traveling salesman problem with time windows (GTSP-TW) to find a sequence of targets and corresponding time windows for the agent to visit. Given such a sequence, the low-level search then finds an associated agent trajectory. To solve the low-level planning problem, we develop a new algorithm called FMC*, which finds a shortest path on a graph of convex sets (GCS) via implicit graph search and pruning techniques specialized for problems with moving targets. We test FMC*-TSP on 280 problem instances with up to 40 targets and demonstrate its smaller median runtime than a baseline based on prior work.

A Complete Algorithm for a Moving Target Traveling Salesman Problem with Obstacles

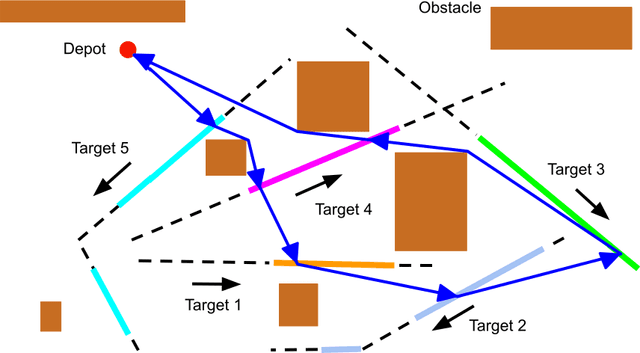
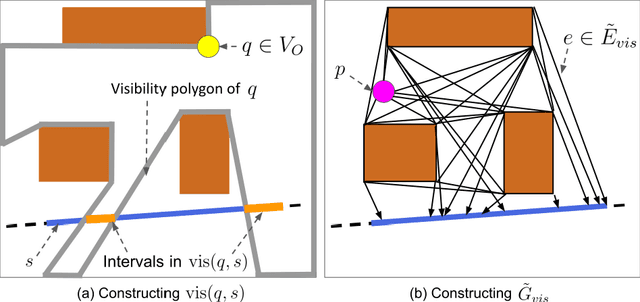
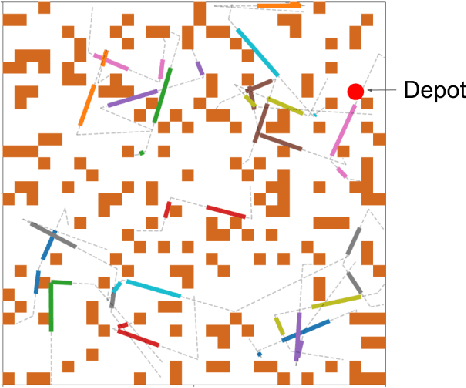
The moving target traveling salesman problem with obstacles (MT-TSP-O) is a generalization of the traveling salesman problem (TSP) where, as its name suggests, the targets are moving. A solution to the MT-TSP-O is a trajectory that visits each moving target during a certain time window(s), and this trajectory avoids stationary obstacles. We assume each target moves at a constant velocity during each of its time windows. The agent has a speed limit, and this speed limit is no smaller than any target's speed. This paper presents the first complete algorithm for finding feasible solutions to the MT-TSP-O. Our algorithm builds a tree where the nodes are agent trajectories intercepting a unique sequence of targets within a unique sequence of time windows. We generate each of a parent node's children by extending the parent's trajectory to intercept one additional target, each child corresponding to a different choice of target and time window. This extension consists of planning a trajectory from the parent trajectory's final point in space-time to a moving target. To solve this point-to-moving-target subproblem, we define a novel generalization of a visibility graph called a moving target visibility graph (MTVG). Our overall algorithm is called MTVG-TSP. To validate MTVG-TSP, we test it on 570 instances with up to 30 targets. We implement a baseline method that samples trajectories of targets into points, based on prior work on special cases of the MT-TSP-O. MTVG-TSP finds feasible solutions in all cases where the baseline does, and when the sum of the targets' time window lengths enters a critical range, MTVG-TSP finds a feasible solution with up to 38 times less computation time.