A Complete Algorithm for a Moving Target Traveling Salesman Problem with Obstacles

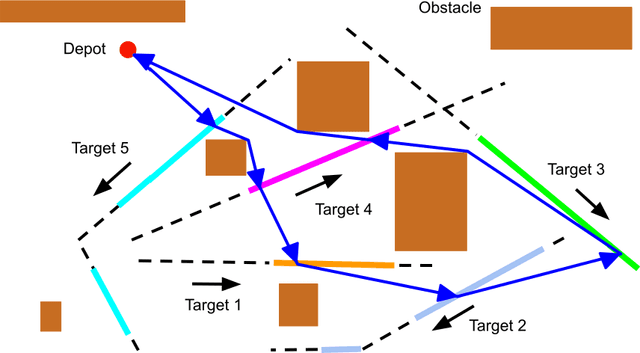
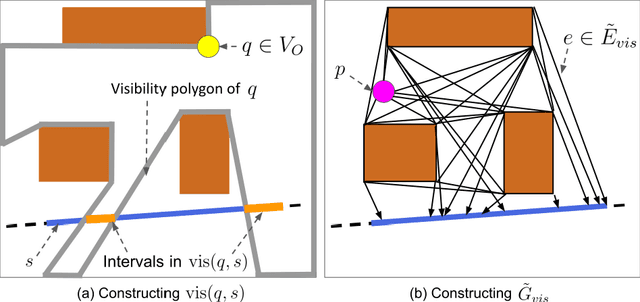
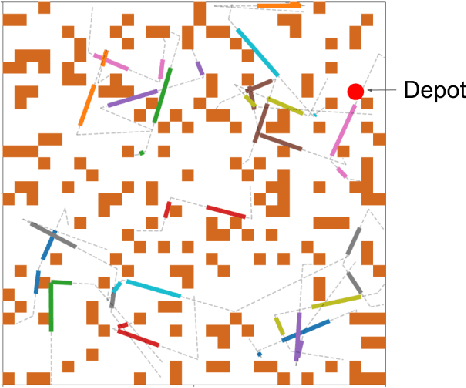
The moving target traveling salesman problem with obstacles (MT-TSP-O) is a generalization of the traveling salesman problem (TSP) where, as its name suggests, the targets are moving. A solution to the MT-TSP-O is a trajectory that visits each moving target during a certain time window(s), and this trajectory avoids stationary obstacles. We assume each target moves at a constant velocity during each of its time windows. The agent has a speed limit, and this speed limit is no smaller than any target's speed. This paper presents the first complete algorithm for finding feasible solutions to the MT-TSP-O. Our algorithm builds a tree where the nodes are agent trajectories intercepting a unique sequence of targets within a unique sequence of time windows. We generate each of a parent node's children by extending the parent's trajectory to intercept one additional target, each child corresponding to a different choice of target and time window. This extension consists of planning a trajectory from the parent trajectory's final point in space-time to a moving target. To solve this point-to-moving-target subproblem, we define a novel generalization of a visibility graph called a moving target visibility graph (MTVG). Our overall algorithm is called MTVG-TSP. To validate MTVG-TSP, we test it on 570 instances with up to 30 targets. We implement a baseline method that samples trajectories of targets into points, based on prior work on special cases of the MT-TSP-O. MTVG-TSP finds feasible solutions in all cases where the baseline does, and when the sum of the targets' time window lengths enters a critical range, MTVG-TSP finds a feasible solution with up to 38 times less computation time.

Measure Preserving Flows for Ergodic Search in Convoluted Environments

Autonomous robotic search has important applications in robotics, such as the search for signs of life after a disaster. When \emph{a priori} information is available, for example in the form of a distribution, a planner can use that distribution to guide the search. Ergodic search is one method that uses the information distribution to generate a trajectory that minimizes the ergodic metric, in that it encourages the robot to spend more time in regions with high information and proportionally less time in the remaining regions. Unfortunately, prior works in ergodic search do not perform well in complex environments with obstacles such as a building's interior or a maze. To address this, our work presents a modified ergodic metric using the Laplace-Beltrami eigenfunctions to capture map geometry and obstacle locations within the ergodic metric. Further, we introduce an approach to generate trajectories that minimize the ergodic metric while guaranteeing obstacle avoidance using measure-preserving vector fields. Finally, we leverage the divergence-free nature of these vector fields to generate collision-free trajectories for multiple agents. We demonstrate our approach via simulations with single and multi-agent systems on maps representing interior hallways and long corridors with non-uniform information distribution. In particular, we illustrate the generation of feasible trajectories in complex environments where prior methods fail.

A Convex Formulation of the Soft-Capture Problem

We present a fast trajectory optimization algorithm for the soft capture of uncooperative tumbling space objects. Our algorithm generates safe, dynamically feasible, and minimum-fuel trajectories for a six-degree-of-freedom servicing spacecraft to achieve soft capture (near-zero relative velocity at contact) between predefined locations on the servicer spacecraft and target body. We solve a convex problem by enforcing a convex relaxation of the field-of-view constraint, followed by a sequential convex program correcting the trajectory for collision avoidance. The optimization problems can be solved with a standard second-order cone programming solver, making the algorithm both fast and practical for implementation in flight software. We demonstrate the performance and robustness of our algorithm in simulation over a range of object tumble rates up to 10{\deg}/s.

Multi-agent Collective Construction using 3D Decomposition

This paper addresses a Multi-Agent Collective Construction (MACC) problem that aims to build a three-dimensional structure comprised of cubic blocks. We use cube-shaped robots that can carry one cubic block at a time, and move forward, reverse, left, and right to an adjacent cell of the same height or climb up and down one cube height. To construct structures taller than one cube, the robots must build supporting stairs made of blocks and remove the stairs once the structure is built. Conventional techniques solve for the entire structure at once and quickly become intractable for larger workspaces and complex structures, especially in a multi-agent setting. To this end, we present a decomposition algorithm that computes valid substructures based on intrinsic structural dependencies. We use Mixed Integer Linear Programming (MILP) to solve for each of these substructures and then aggregate the solutions to construct the entire structure. Extensive testing on 200 randomly generated structures shows an order of magnitude improvement in the solution computation time compared to an MILP approach without decomposition. Additionally, compared to Reinforcement Learning (RL) based and heuristics-based approaches drawn from the literature, our solution indicates orders of magnitude improvement in the number of pick-up and drop-off actions required to construct a structure. Furthermore, we leverage the independence between substructures to detect which sub-structures can be built in parallel. With this parallelization technique, we illustrate a further improvement in the number of time steps required to complete building the structure. This work is a step towards applying multi-agent collective construction for real-world structures by significantly reducing solution computation time with a bounded increase in the number of time steps required to build the structure.