Tightest Admissible Shortest Path

The shortest path problem in graphs is fundamental to AI. Nearly all variants of the problem and relevant algorithms that solve them ignore edge-weight computation time and its common relation to weight uncertainty. This implies that taking these factors into consideration can potentially lead to a performance boost in relevant applications. Recently, a generalized framework for weighted directed graphs was suggested, where edge-weight can be computed (estimated) multiple times, at increasing accuracy and run-time expense. We build on this framework to introduce the problem of finding the tightest admissible shortest path (TASP); a path with the tightest suboptimality bound on the optimal cost. This is a generalization of the shortest path problem to bounded uncertainty, where edge-weight uncertainty can be traded for computational cost. We present a complete algorithm for solving TASP, with guarantees on solution quality. Empirical evaluation supports the effectiveness of this approach.

A Generalization of the Shortest Path Problem to Graphs with Multiple Edge-Cost Estimates

The shortest path problem in graphs is a cornerstone for both theory and applications. Existing work accounts for edge weight access time, but generally ignores edge weight computation time. In this paper we present a generalized framework for weighted directed graphs, where each edge cost can be dynamically estimated by multiple estimators, that offer different cost bounds and run-times. This raises several generalized shortest path problems, that optimize different aspects of path cost while requiring guarantees on cost uncertainty, providing a better basis for modeling realistic problems. We present complete, anytime algorithms for solving these problems, and provide guarantees on the solution quality.

Rivendell: Project-Based Academic Search Engine

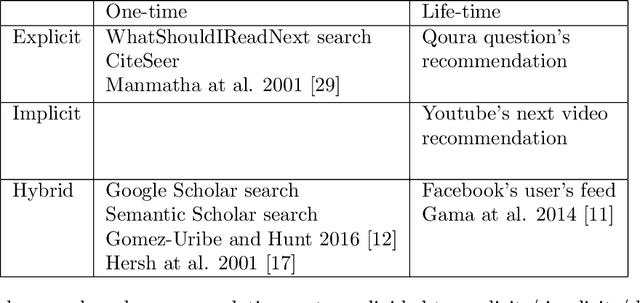
Finding relevant research literature in online databases is a familiar challenge to all researchers. General search approaches trying to tackle this challenge fall into two groups: one-time search and life-time search. We observe that both approaches ignore unique attributes of the research domain and are affected by concept drift. We posit that in searching for research papers, a combination of a life-time search engine with an explicitly-provided context (project) provides a solution to the concept drift problem. We developed and deployed a project-based meta-search engine for research papers called Rivendell. Using Rivendell, we conducted experiments with 199 subjects, comparing project-based search performance to one-time and life-time search engines, revealing an improvement of up to 12.8 percent in project-based search compared to life-time search.

Position Paper: Online Modeling for Offline Planning

The definition and representation of planning problems is at the heart of AI planning research. A key part is the representation of action models. Decades of advances improving declarative action model representations resulted in numerous theoretical advances, and capable, working, domain-independent planners. However, despite the maturity of the field, AI planning technology is still rarely used outside the research community, suggesting that current representations fail to capture real-world requirements, such as utilizing complex mathematical functions and models learned from data. We argue that this is because the modeling process is assumed to have taken place and completed prior to the planning process, i.e., offline modeling for offline planning. There are several challenges inherent to this approach, including: limited expressiveness of declarative modeling languages; early commitment to modeling choices and computation, that preclude using the most appropriate resolution for each action model -- which can only be known during planning; and difficulty in reliably using non-declarative, learned, models. We therefore suggest to change the AI planning process, such that is carries out online modeling in offline planning, i.e., the use of action models that are computed or even generated as part of the planning process, as they are accessed. This generalizes the existing approach (offline modeling). The proposed definition admits novel planning processes, and we suggest one concrete implementation, demonstrating the approach. We sketch initial results that were obtained as part of a first attempt to follow this approach by planning with action cost estimators. We conclude by discussing open challenges.

Planning with Dynamically Estimated Action Costs

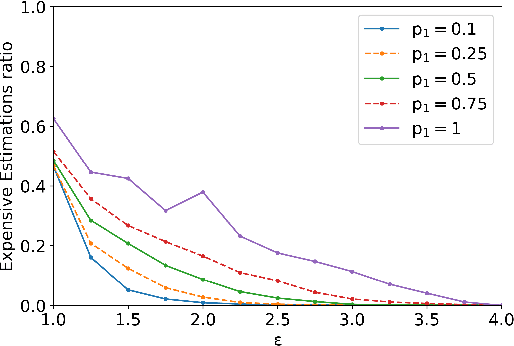
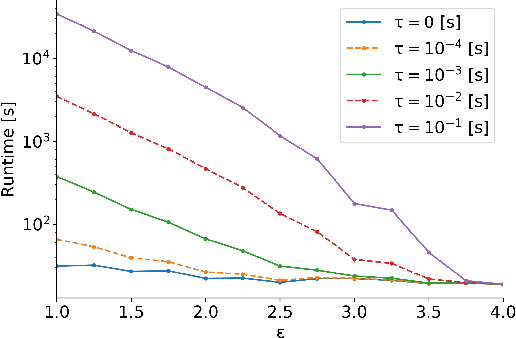
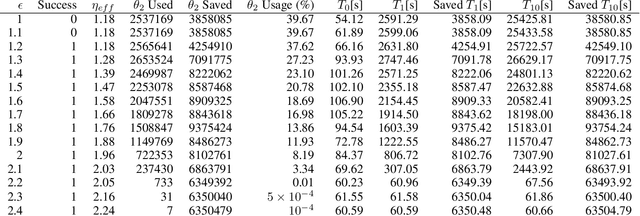
Information about action costs is critical for real-world AI planning applications. Rather than rely solely on declarative action models, recent approaches also use black-box external action cost estimators, often learned from data, that are applied during the planning phase. These, however, can be computationally expensive, and produce uncertain values. In this paper we suggest a generalization of deterministic planning with action costs that allows selecting between multiple estimators for action cost, to balance computation time against bounded estimation uncertainty. This enables a much richer -- and correspondingly more realistic -- problem representation. Importantly, it allows planners to bound plan accuracy, thereby increasing reliability, while reducing unnecessary computational burden, which is critical for scaling to large problems. We introduce a search algorithm, generalizing $A^*$, that solves such planning problems, and additional algorithmic extensions. In addition to theoretical guarantees, extensive experiments show considerable savings in runtime compared to alternatives.

Heuristic Online Goal Recognition in Continuous Domains

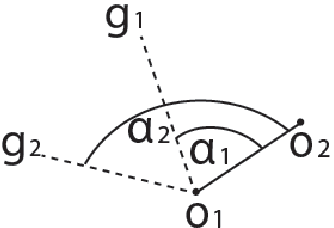
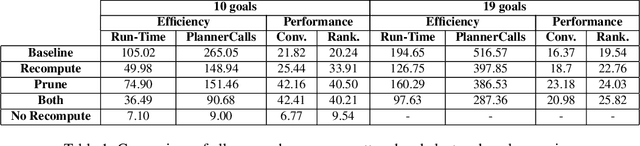
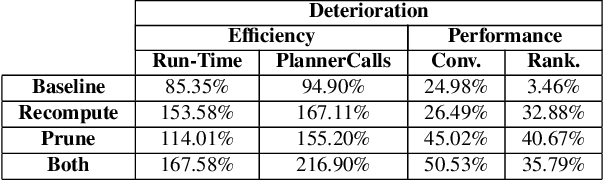
Goal recognition is the problem of inferring the goal of an agent, based on its observed actions. An inspiring approach - plan recognition by planning (PRP) - uses off-the-shelf planners to dynamically generate plans for given goals, eliminating the need for the traditional plan library. However, existing PRP formulation is inherently inefficient in online recognition, and cannot be used with motion planners for continuous spaces. In this paper, we utilize a different PRP formulation which allows for online goal recognition, and for application in continuous spaces. We present an online recognition algorithm, where two heuristic decision points may be used to improve run-time significantly over existing work. We specify heuristics for continuous domains, prove guarantees on their use, and empirically evaluate the algorithm over hundreds of experiments in both a 3D navigational environment and a cooperative robotic team task.

Multi-Robot Adversarial Patrolling: Facing a Full-Knowledge Opponent

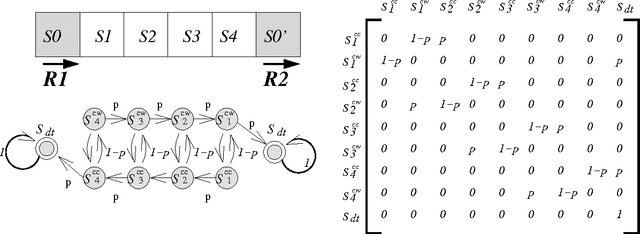
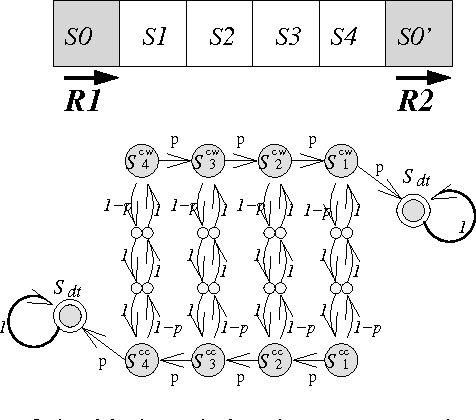
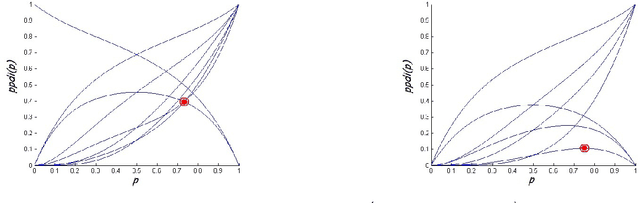
The problem of adversarial multi-robot patrol has gained interest in recent years, mainly due to its immediate relevance to various security applications. In this problem, robots are required to repeatedly visit a target area in a way that maximizes their chances of detecting an adversary trying to penetrate through the patrol path. When facing a strong adversary that knows the patrol strategy of the robots, if the robots use a deterministic patrol algorithm, then in many cases it is easy for the adversary to penetrate undetected (in fact, in some of those cases the adversary can guarantee penetration). Therefore this paper presents a non-deterministic patrol framework for the robots. Assuming that the strong adversary will take advantage of its knowledge and try to penetrate through the patrols weakest spot, hence an optimal algorithm is one that maximizes the chances of detection in that point. We therefore present a polynomial-time algorithm for determining an optimal patrol under the Markovian strategy assumption for the robots, such that the probability of detecting the adversary in the patrols weakest spot is maximized. We build upon this framework and describe an optimal patrol strategy for several robotic models based on their movement abilities (directed or undirected) and sensing abilities (perfect or imperfect), and in different environment models - either patrol around a perimeter (closed polygon) or an open fence (open polyline).