Tightest Admissible Shortest Path

The shortest path problem in graphs is fundamental to AI. Nearly all variants of the problem and relevant algorithms that solve them ignore edge-weight computation time and its common relation to weight uncertainty. This implies that taking these factors into consideration can potentially lead to a performance boost in relevant applications. Recently, a generalized framework for weighted directed graphs was suggested, where edge-weight can be computed (estimated) multiple times, at increasing accuracy and run-time expense. We build on this framework to introduce the problem of finding the tightest admissible shortest path (TASP); a path with the tightest suboptimality bound on the optimal cost. This is a generalization of the shortest path problem to bounded uncertainty, where edge-weight uncertainty can be traded for computational cost. We present a complete algorithm for solving TASP, with guarantees on solution quality. Empirical evaluation supports the effectiveness of this approach.

A Generalization of the Shortest Path Problem to Graphs with Multiple Edge-Cost Estimates

The shortest path problem in graphs is a cornerstone for both theory and applications. Existing work accounts for edge weight access time, but generally ignores edge weight computation time. In this paper we present a generalized framework for weighted directed graphs, where each edge cost can be dynamically estimated by multiple estimators, that offer different cost bounds and run-times. This raises several generalized shortest path problems, that optimize different aspects of path cost while requiring guarantees on cost uncertainty, providing a better basis for modeling realistic problems. We present complete, anytime algorithms for solving these problems, and provide guarantees on the solution quality.

Position Paper: Online Modeling for Offline Planning

The definition and representation of planning problems is at the heart of AI planning research. A key part is the representation of action models. Decades of advances improving declarative action model representations resulted in numerous theoretical advances, and capable, working, domain-independent planners. However, despite the maturity of the field, AI planning technology is still rarely used outside the research community, suggesting that current representations fail to capture real-world requirements, such as utilizing complex mathematical functions and models learned from data. We argue that this is because the modeling process is assumed to have taken place and completed prior to the planning process, i.e., offline modeling for offline planning. There are several challenges inherent to this approach, including: limited expressiveness of declarative modeling languages; early commitment to modeling choices and computation, that preclude using the most appropriate resolution for each action model -- which can only be known during planning; and difficulty in reliably using non-declarative, learned, models. We therefore suggest to change the AI planning process, such that is carries out online modeling in offline planning, i.e., the use of action models that are computed or even generated as part of the planning process, as they are accessed. This generalizes the existing approach (offline modeling). The proposed definition admits novel planning processes, and we suggest one concrete implementation, demonstrating the approach. We sketch initial results that were obtained as part of a first attempt to follow this approach by planning with action cost estimators. We conclude by discussing open challenges.

Planning with Dynamically Estimated Action Costs

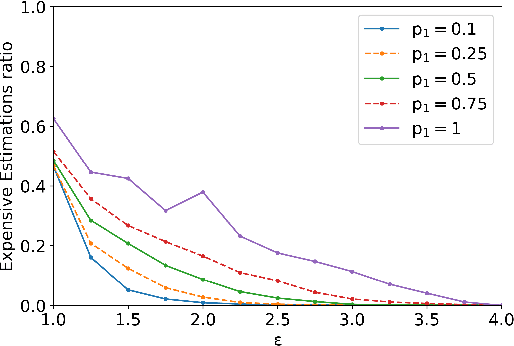
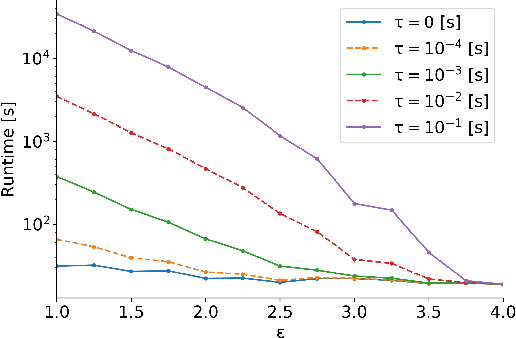
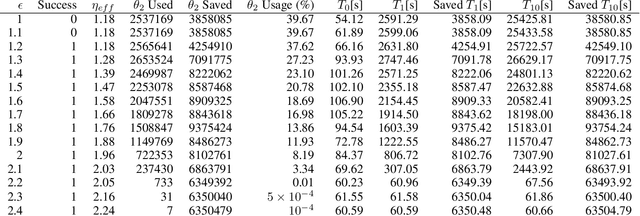
Information about action costs is critical for real-world AI planning applications. Rather than rely solely on declarative action models, recent approaches also use black-box external action cost estimators, often learned from data, that are applied during the planning phase. These, however, can be computationally expensive, and produce uncertain values. In this paper we suggest a generalization of deterministic planning with action costs that allows selecting between multiple estimators for action cost, to balance computation time against bounded estimation uncertainty. This enables a much richer -- and correspondingly more realistic -- problem representation. Importantly, it allows planners to bound plan accuracy, thereby increasing reliability, while reducing unnecessary computational burden, which is critical for scaling to large problems. We introduce a search algorithm, generalizing $A^*$, that solves such planning problems, and additional algorithmic extensions. In addition to theoretical guarantees, extensive experiments show considerable savings in runtime compared to alternatives.

Low power in-situ AI Calibration of a 3 Axial Magnetic Sensor

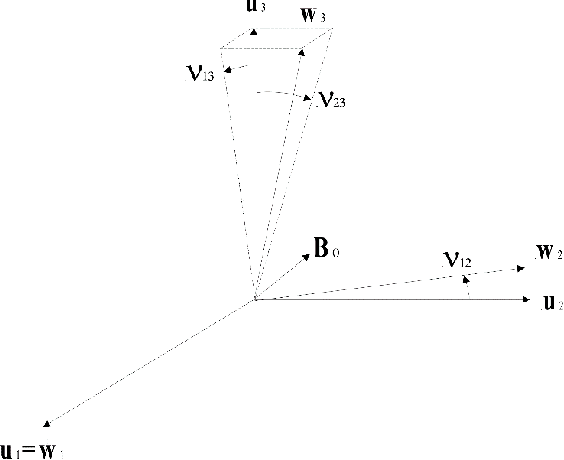
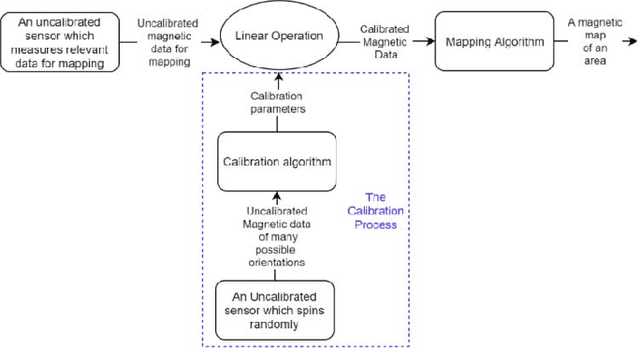
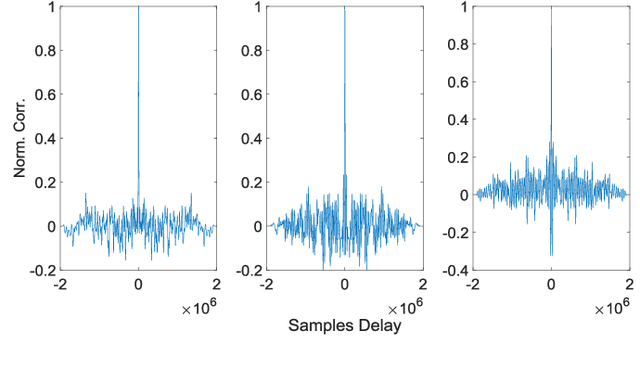
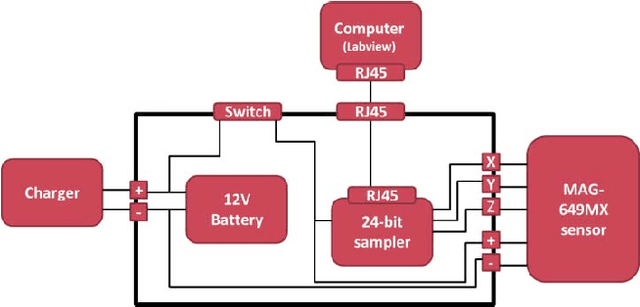
Magnetic surveys are conventionally performed by scanning a domain with a portable scalar magnetic sensor. Unfortunately, scalar magnetometers are expensive, power consuming and bulky. In many applications, calibrated vector magnetometers can be used to perform magnetic surveys. In recent years algorithms based on artificial intelligence (AI) achieve state-of-the-art results in many modern applications. In this work we investigate an AI algorithm for the classical scalar calibration of magnetometers. A simple, low cost method for performing a magnetic survey is presented. The method utilizes a low power consumption sensor with an AI calibration procedure that improves the common calibration methods and suggests an alternative to the conventional technology and algorithms. The setup of the survey system is optimized for quick deployment in-situ right before performing the magnetic survey. We present a calibration method based on a procedure of rotating the sensor in the natural earth magnetic field for an optimal time period. This technique can deal with a constant field offset and non-orthogonality issues and does not require any external reference. The calibration is done by finding an estimator that yields the calibration parameters and produces the best geometric fit to the sensor readings. A comprehensive model considering the physical, algorithmic and hardware properties of the magnetometer of the survey system is presented. The geometric ellipsoid fitting approach is parametrically tested. The calibration procedure reduced the root-mean-squared noise from the order of 104 nT to less than 10 nT with variance lower than 1 nT in a complete 360 degrees rotation in the natural earth magnetic field.

Machine Learning Detection Algorithm for Large Barkhausen Jumps in Cluttered Environment

Modern magnetic sensor arrays conventionally utilize state of the art low power magnetometers such as parallel and orthogonal fluxgates. Low power fluxgates tend to have large Barkhausen jumps that appear as a dc jump in the fluxgate output. This phenomenon deteriorates the signal fidelity and effectively increases the internal sensor noise. Even if sensors that are more prone to dc jumps can be screened during production, the conventional noise measurement does not always catch the dc jump because of its sparsity. Moreover, dc jumps persist in almost all the sensor cores although at a slower but still intolerable rate. Even if dc jumps can be easily detected in a shielded environment, when deployed in presence of natural noise and clutter, it can be hard to positively detect them. This work fills this gap and presents algorithms that distinguish dc jumps embedded in natural magnetic field data. To improve robustness to noise, we developed two machine learning algorithms that employ temporal and statistical physical-based features of a pre-acquired and well-known experimental data set. The first algorithm employs a support vector machine classifier, while the second is based on a neural network architecture. We compare these new approaches to a more classical kernel-based method. To that purpose, the receiver operating characteristic curve is generated, which allows diagnosis ability of the different classifiers by comparing their performances across various operation points. The accuracy of the machine learning-based algorithms over the classic method is highly emphasized. In addition, high generalization and robustness of the neural network can be concluded, based on the rapid convergence of the corresponding receiver operating characteristic curves.